基于时钟合成的高速任意波形数字信号产生方法

贺 庆,郝思聪

(北京信息科技大学 仪器科学与光电工程学院，北京 100192)

0 引言

任意波形发生器是现代电子测量中常用的信号源[1-4]。它既可以产生常规的函数波形，也可以产生用户自定义的任意波形[5-6]。任意波形发生器输出信号的灵活性使之成为生产、教学、科研中应用广泛的通用测试仪器之一。随着科技的发展，对任意波形发生器的性能提出了更高的要求。

目前任意波形发生器普遍基于直接数字合成(direct digital synthesis，DDS)技术设计实现[7-10]。直接数字合成技术的原理是基于存储技术和取样技术,通过以采样时钟频率对频率控制字进行循环累加，按累加结果对存储有信号波形幅值的查找表进行寻址，最终得到频率和相位实时可调的数字波形信号。DDS技术具有频率切换快，分辨率高，输出信号相位连续等特点。但它输出信号的最高频率往往受到客观条件的限制。为此，电子科技大学的田书林等[11]、贺庆等[12]提出了多DAC(digital analog convertor,数模转换器)伪差值法及分相存储波形合成方法，有效提高了输出信号的最高频率。然而，一方面这两种方法分别需要多路DAC和多路RAM(random access memory，随机存取存储器)，增加了系统的复杂度，另一方面两种方法对波形信号进行合成，对合成器的工作频率和处理负荷要求较高。尽管后续有研究优化了分相存储法累加器的逻辑资源开销[13]，但并串转换器不可避免地长时间工作于最高频率。

本文提出了一种时钟合成的方法以扩展任意波形发生器输出信号频率范围。首先通过DDS原理产生可控频率的方波，然后对其进行分相合成，提高方波最大输出频率。利用该方波作为可变时钟源，对相位步进值进行累加，累加结果对波形查找表进行寻址，得到高速任意波形输出。通过改变信号采样时钟频率的方法，实现不同频率任意波形数字信号的生成。为了便于工程应用中进行参数选择和误差评估，进行了参数分析和杂散误差分析，为低杂散设计提供了理论依据。经FPGA(field-programmable gate array,现场可编程门陈列)中仿真验证，此方法有效提高了系统的采样速率，扩宽了输出信号频率，同时可具有较高的频率分辨率和相位分辨率。相对于传统DDS算法，处理器的运算负荷大大降低。

1 产生时钟合成的两级DDS结构

传统的DDS技术主要由相位累加器、波形查找表、DAC及低通滤波器等组成。N位相位累加器在取样时钟fc激励下，以频率控制字K所决定的相位增量进行累加，并以每次的累加结果作为波形查找表的地址取出波形数据，得到所需波形的数字信号。其输出信号频率为

(1)

通常取样时钟fc和相位累加器的位数N是固定不变的，通过改变频率控制字K实现对输出波形频率的改变。而本文方法，则是通过改变取样时钟的频率fc实现对波形输出频率的控制。由两级DDS结构实现：时钟DDS和主DDS。时钟DDS负责根据频率控制字合成可变频率的方波，作为主DDS的取样时钟。主DDS在时钟DDS输出的方波激励下，对相位步进值M进行累加及对波形查找表进行寻址。其系统结构如图1所示。

首先时钟DDS产生0～1输出的方波信号，以系统时钟频率fi对频率控制字K进行累加，累加结果A经时钟合成模块分相、合成后得到取样时钟fc。以四分相为例，时钟合成模块的结构如图2所示。

时钟合成模块包括分相加法器，方波查找表和选通合成模块。设时钟DDS累加器累加结果为A，经加法器后，得到4路相位间隔相等的相位字，分别为:A,A+K/4,A+K/2,A+3K/4。利用相位字对方波查找表进行寻址得到4路等相位间隔的0～1方波。选通合成模块，将4路方波信号排列依次输出，组合成一路高速方波信号。由于方波的幅值只需0、1两个值，因此查找表不需要占用存储空间，设定好判断条件即可。根据文献[16]中理论，时钟合成模块相当于在每个系统时钟fi内，对合成方波信号增加为4倍的采样点。故输出频率为

(2)

根据奈奎斯特取样定理，频率控制字K的取值范围为[0,2N+1]。当K=2N+1时，合成0～1方波信号得到最大频率为2×fi。

然后，在主DDS中，用合成的0～1方波信号作为取样时钟，对相位步进值M进行累加。以频率fc依次提取出查找表中的波形各点幅值，从而得到波形数字信号，输出信号频率为

(3)

式中N′为主DDS的相位累加器位数，应与主DDS中的查找表位数相同。需注意的是，根据奈奎斯特取样定理，对于正弦波，M取值范围是[1,2N′-1)；而对于用户自定义的任意波形，为了保证信号的波形有效相位信息不丢失，M应等于1。

将波形数字信号经过DAC转换为量化模拟信号，再经滤波器滤除数字噪声后得到所需频率的波形模拟信号。本文重点讨论波形数字信号的生成部分。

2 参数及误差分析

2.1 参数分析

在本方法中，频率控制字K决定了主DDS中的取样频率。对于任意波形输出而言，由公式(3)可知，频率控制字K决定了最终任意波形输出信号的频率。K越大，输出频率fo越快，两者呈线性关系。当K=2N+1时，输出信号频率fo最大为fi/2N′-1。而当K=0时，输出信号频率为0，此时FPGA输出直流信号。根据式(3)得

(4)

系统时钟频率fi同样决定了输出信号的频率。fi越大，输出频率越快。在具体设计中，系统时钟往往是固定值。为了输出频率更快，可以将FPGA输入时钟经锁相环倍频至可达到的最快频率，作为系统时钟fi。

相位累加器1的位数N′应与任意波形查找表的地址位数相同，由用户定义的任意波形数据个数决定。位数越多，相位分辨率越高，所能表现的任意波形特征越丰富，相应的输出任意波形信号周期越长，频率越慢。

相位累加器2的位数N，决定了输出信号的频率分辨率。输出信号的频率分辨率为fi/2N′+N。N值越大，频率分辨率越高。虽然N′的取值也会影响到频率分辨率，但N′会影响任意波形信号最高频率，因此不建议通过提高N′来提高输出信号频率分辨率。由于K的取值范围最大可到2N+1，因此无论N取值多少，对最终的输出频率没有影响。

对于函数波形而言，M可取大于1的数值，以提高信号输出频率。但由于M大于1时，会造成信号有效相位缺失，可能会影响信号的幅度、占空比等性能。因此尽可能通过调节K来调节信号输出频率。只有当所需输出信号频率大于fi/2N′-1时，才需要M取大于1的数值。

输出任意波形的幅度分辨率与主DDS任意波形查找表的数据位数一致。数据位数越高，幅度分辨率越高，所需的DAC位数也越高。而时钟DDS输出方波因只做任意波形的取样时钟用，幅度位数只需要1位(0～1)即可。

2.2 误差分析

DDS具有全数字化带来的优点，同时也引进了数字化结构的缺点：具有输出杂散[14]。根据本文提出方法，波形发生器数字部分的杂散主要有两个方面：

1)相位截断误差。由于波形存储器的容量有限，相位分辨率只有2π/2N′。因此相邻相位点之间的波形值被忽略，即时钟累加器中的N位累加值无法体现，从而产生截断误差。

2)幅度量化误差。由于DAC的位数有限，因此对于波形的幅值分辨率有限。设采用无符号二进制数值方式，DAC位数为L，则波形幅值表示范围为[0,2L-1]，归一化幅度的分辨率为1/(2L-1)。通常波形存储器的数据有效位数与DAC的一致。对于小于幅度分辨率的幅度细节进行舍入或截尾处理，从而造成幅度量化误差。实际中多采用舍入处理方式。

作为工程简化，本文以正弦波为例，进行误差分析，以期对参数的选择提供依据。设DDS产生的数字波形序列为x(n)，时钟累加器和主累加器的初始相位分别为P1和P2。则其理想情况下：

(5)

经相位截断和幅度量化后实际为

(6)

式中：round表示四舍五入取整函数；floor表示向下取整函数；P1取值范围为[0，2N-1]，P2取值范围为[0，2N′-1]。由此，归一化误差e(n)为

(7)

e(n)可以分解为由相位截断引起的误差序列et(n)和由幅度量化引起的误差序列er(n)，两者表达式分别为：

(8)

(9)

当K为奇数时，et(n)和er(n)的周期取最大值为lcm(2N′+N，M)/M，式中lcm为最小公倍数函数。在输出频率区间[0，2πfc)内，et(n)和er(n)会有lcm(2N′+N,M)/M个频率分量。由于为了提高频率分辨率，N往往很大，进行频域分析的计算量较大。因此为了减少杂散和便于误差评估，K尽可能取与目标频率相近的偶数值。

当K为2N的m倍时(m为1或2)，et(n)和er(n)周期取得最小值lcm(2N′,M)/(mM)。此时，在输出频率区间[0，2πfc)内，et(n)和er(n)会有lcm(2N′，M)/(mM)个频率分量，可进行DFT(离散傅立叶变换)求出每个频率分量幅度。P2仅决定et(n)和er(n)的相位，对其幅值没有影响。et(n)的幅度随P1/2N和M/2N′呈单调递增变化。由式(8)可知，当P1=0时，相位截断误差序列et(n)为0。因此，为了误差最小，在进行频率切换时，可以令P1清零，此时因P2保持不变，输出信号x(n)相位仍然连续。P1/2N对er(n)无影响。M/2N′影响er(n)的周期，对幅度几乎没有影响。er(n)的幅度主要受L的影响。

现有DAC的位数L取值范围通常在[8,16]，令式(9)中的floor[(nK+P1)/2N]M/2N′+P2/2N′等于δ，可仿真出，在其他变量不变情况下，er(δ)的幅度随L变化的规律如图3所示。

由图3可知，当L越大时，幅度量化误差越小，但变小的趋势逐渐放缓。达到一定位数后，误差变化不大。因此应根据实际应用需要在复杂度和量化误差间折中选择。

两种杂散中，通常相位截断误差要大于幅度量化误差。除上述两种数字误差之外，DDS还包括DAC的各种非线性效应造成的杂散频率分量(杂散功率通常集中在输出信号的各次谐波上)和参考时钟引入的杂散(时钟泄露和时钟相位噪声)，这些杂散多为高频噪声，可通过DAC之后接低通滤波器进行滤除。

3 实验验证

通过在FPGA中模拟仿真，验证所提出的方法的有效性。FPGA采用Altera公司的EP2C70F896C6型号芯片，输入时钟为100 MHz时，其锁相环输出上限频率为500 MHz，为扩大输出信号频率范围，实验采用500 MHz作为时钟DDS的取样时钟fi。

3.1 任意波形验证

在FPGA中，划出一块RAM存储空间存储自定义的任意波形数据。本例中，存储的任意波形点数为32，数据宽度10 bit。各点数值大小如表1所示。

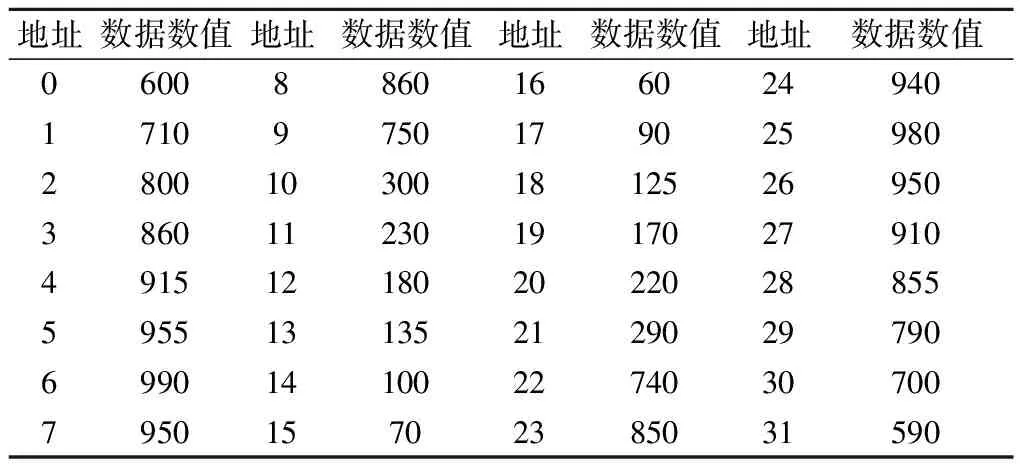
表1 任意波形数据表

利用本文提出的方法分别仿真频率为31.25 MHz、23.438 MHz和15.625 MHz任意波形的产生。为保证任意波形有效相位不丢失，相位步进值M设为1，主DDS累加器位数N′为5。为实现较高的频率分辨率，时钟DDS累加器位数N设为46，则频率分辨率约为2.22×10-7Hz。由式(3)计算可得，在输入系统时钟fi为500 MHz时，频率控制字K依次为247，3×245，246。全编译后，仿真结果如图4(a)所示。从图中可以看出，该方法实现了任意波形频率实时可调，切换速度快，切换时相位连续。生成信号的周期符合预期目标。作为对比，采用常规DDS方法，在固定取样时钟为500 MHz时，依次生成3种频率的任意波形。结果如图4(b)所示。

从图中对比可知，在31.25 MHz、23.438 MHz两种情况下，采用常规DDS实现的任意波形发生了畸变，丢失了部分相位信息。只有在15.625 MHz时，任意波形的数据完整。由于采样率限制，常规方法每2 ns更新一个数据点。而采用本文方法，在最高输出频率下，每1 ns更新一个数据点，相当于采样率为1 GHz。而相比于1 GHz采样率的系统，本方法对器件要求低，只需锁相环上限频率为500 MHz的FPGA即可完成。另一方面传统方法即使产生低速信号时，全累加器和DAC仍需工作在1 GHz采样率，而本方法主累加器工作频率根据输出信号频率可快可慢，仅在最高频率下，对5位深度的累加器进行1 GHz高速累加，即可达到51位深度累加器同样的频率分辨率，大大降低了处理器的运算负荷。

3.2 正弦波形验证

本例中，以正弦信号为代表，验证本文方法对于函数波形的实现效果。调用Quartus中的RAM软核，存储16位深度、10位宽度的正弦波数据。利用本文方法依次产生400 MHz、250 MHz、125 MHz、62.5 MHz和31.25 MHz正弦波形。根据第2章方法，主DDS的累加器位数N′为16，时钟DDS累加器位数N设为30。正弦信号频谱单一，据计算，实验所需输出频率均大于fi/2N′-1，因此M可取大于1的值。根据式(3)计算可得，频率控制字K为231，5个输出频率对应的M值依次为26 214、16 384、8 192、4 096、2 046。仿真结果如图5所示。

由图可见，切换M值，波形输出频率实时改变，切换时相位连续。当产生400 MHz正弦波时，平均每周期只取2.5个样点，因此波形幅度衰减明显。而输出频率为250 MHz时，每周期可取4个样点，波形幅度与正常无异。但正弦波形仍不明显，需FPGA后级模拟滤波器滤除数字噪声，实现正弦波形。随着M值变小，每周期取的样点数越多，正弦波形越平滑完整。波形的相位分辨率与存储器深度有关，本例中精确到0.005 5°。如外扩大容量存储器，可实现更高的相位精度。

4 结束语

本文提出了一种高速任意波形产生的新方法。该方法通过两级DDS结构实现：第一级DDS负责产生高速的可变时钟，第二级DDS按照传统方法在可变时钟驱动下产生所需任意波形。分析了该设计的参量对波形性能和杂散误差的影响。通过两个实例验证了本文方法的有效性。经仿真验证，本文方法具有输出波形频率高，运算负荷小，不需要增加多余器件的优势。同时兼具了DDS本身具有的频率实时可调、切换速度快及相位连续的特点。保留任意波形的全部有效相位信息的同时，可实现较高的频率分辨率和相位分辨率。