刹车盘摩擦副滑摩过程温度场分析

李 进，李 乐，吴健鹏

(北京信息科技大学 现代测控技术教育部重点实验室，北京 100192)

0 引言

盘式制动器在车辆制动系统中应用十分广泛，其核心部件包括刹车盘和刹车片，其中刹车盘的性能对车辆制动系统产生直接影响。盘式制动器利用刹车片与刹车盘之间的接合压力产生制动力矩，使车辆停止。车辆制动期间系统动能转化为热能，制动器摩擦副表面产生大量摩擦热，热能的积累使摩擦副局部温度急剧升高，导致摩擦界面温度场分布不均匀，刹车盘巨大的温度差导致其内部热应力分布不均匀，从而产生热变形甚至热裂纹[1-2]，这是影响摩擦副摩擦学行为的重要因素之一。因此，研究刹车盘滑摩过程的温度场特性对提升刹车盘的工作性能具有重要意义。

针对上述刹车盘摩擦副的热失效现象，国内外学者展开了广泛的研究。王欲进等[3]对刹车盘的厚度变化和温度场的分布进行仿真，使用了基于交错接触的中间处理器处理数据结果。陈友飞[4]建立了有限差分模型，对单次紧急制动工况和多次循环制动工况进行仿真，分析了瞬态温度场、接触压力场和应力场的分布规律，探讨了刹车盘在交变应力作用下产生径向裂纹的原因。余为高[5]探究了刹车盘由于热源位置改变和对流换热作用所形成的不同温度场特性，分析了刹车盘径向热裂纹产生的原因，并采用Coffin-Manson公式预测刹车盘热疲劳寿命。张立军等[6-7]建立了热-机耦合有限元模型，通过改变制动器相关结构参数，分析了不同结构参数对热-机耦合的影响。Kennedy[8]研究了湿式多片制动器轴对称模型的瞬态热弹性问题。Refaat等[9]采用快速傅立叶变换和有限元法研究了盘式制动器三维模型的瞬态热弹性问题。Simo等[10]对盘式制动器摩擦材料的热弹性进行了分析，研究了材料的刚度和弹性对温度场和接触压力场的影响。以上研究，结合不同的工况条件和刹车盘结构参数，分析了刹车盘的温度场和应力场的分布规律以及刹车盘的失效机理。

基于以上研究，本文根据盘式制动器的结构特点，基于ABAQUS建立了刹车盘摩擦副有限元模型，分析了制动压力和对流换热系数对刹车盘界面温度场变化过程的影响规律，并对水冷和风冷两种方式的冷却效果进行了对比。

1 数学模型建立

1.1 热传导模型

盘式制动器摩擦副主要由刹车盘和刹车片组成，其结构如图1所示。

摩擦副结合时，刹车片固定，在刹车片上表面均匀施加外压力，刹车盘与刹车片逐渐压紧，同时由于盘-片间产生相对滑动生成摩擦热。在直角坐标系下，热流密度为

q(x,y,z,t)=μ(Δω)Pi(x,y,z,t)Δω·r

(1)

式中：q为单位面积某点热流密度；μ为摩擦因数；Pi为该点的接触比压；Δω为刹车盘与刹车片的转速差；r为任意点距摩擦副中心的半径。

摩擦副滑摩过程中整个接触面输入的总热流为

(2)

式中：re和ro分别为摩擦接触面的内径和外径；dA=ΔL(dr)/2，其中ΔL为摩擦片的内外弧长之差，表达式为ΔL=Lo-Le。

滑摩过程中某一时刻产生的总热量为

(3)

式中，to、ti分别为摩擦副滑摩开始时刻和结束时刻。

在温度连续的情况下，引入分配系数Kq[11]来表征流入刹车盘与刹车片的热量分配关系。分配系数Kq与刹车盘和刹车片的物理属性有关，表达式为

(4)

式中：qp、qd为输入的热通量；λp、λd为导热系数；ρp、ρd为密度；cp、cd为比热容；下标d和p分别表示刹车盘和刹车片。

由于刹车盘和刹车片的热量分配系数不同，二者之间存在温度差，必然导致热量转移的发生。可以把热传导的过程当作平壁导热过程进行求解，满足傅立叶定律：

(5)

式中：qr为热传导换热量；T1-T2为摩擦面表面温度差；K为材料的热传导系数；A为导热面积。

1.2 几何模型与材料特性

根据常用汽车盘式制动器的实际尺寸，设定刹车盘的内径与外径分别为100 mm和135 mm，厚度为6 mm；刹车片内外径分别为101.5 mm和133 mm，厚度为10 mm，圆心角为30°[12]，盘式制动器摩擦副有限元模型如图2所示。

盘式制动器的刹车盘和刹车片分别为钢和树脂基复合材料，材料属性如表1所示[13]。

表1 摩擦副材料属性参数(20℃)

在模拟过程中，假设摩擦材料各向同性，摩擦过程中温升明显，则摩擦系数和钢片材料的弹性模量与热膨胀系数随温度变化情况如表2所示[13]。

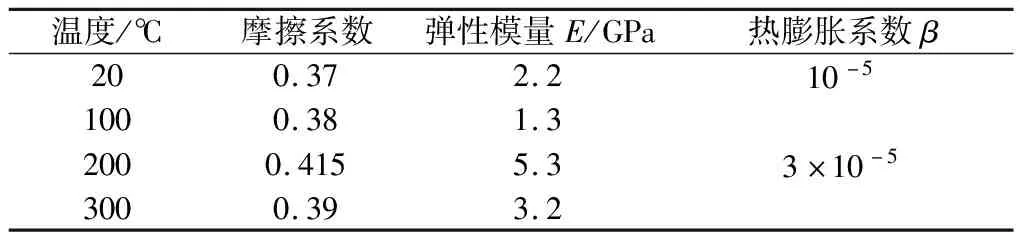
表2 摩擦系数和摩擦片材料性能随温度变化情况

1.3 边界条件

1.3.1 运动与压力加载条件

根据摩擦副实际接合过程，设置有限元模型中，刹车片与刹车盘接触面法向与Z轴平行，如图2所示。刹车片在制动过程中仅能沿Z轴移动，约束其在X与Y方向移动和绕X、Y、Z轴转动5个自由度。同时，刹车盘在制动过程中仅设置绕Z轴的旋转速度，限制其在X、Y、Z方向平移和绕X、Y、Z轴转动5个自由度。对刹车片上表面均匀施加17 MPa的制动压力，在接合0.001 s后，压力呈线性增长到达峰值后保持不变。参考汽车盘式制动器工作的常见工况，设置刹车盘转动的初速度为31.4 rad/s[12]，受计算机性能的限制，研究制动时间为0.27 s内的盘面温度、应力和应变的变化过程。在0.27 s内，刹车盘绕Z轴旋转3圈。

1.3.2 对流换热系数

制动器摩擦副与空气存在对流换热作用，对于刹车盘表面的对流换热系数，具体的计算方法如下[14]。

首先计算雷诺数Re：

Re=νρara/(3.6μa)

(6)

式中：ρa和μa分别为空气的密度和粘度；ra为刹车盘的外径；ν为空气流速。然后根据雷诺数大小，采用如下公式计算出对应的对流换热系数：

(7)

式中λa为空气的导热系数。

2 有限元模拟结果及分析

采用ABAQUS软件进行刹车盘摩擦副滑摩过程的热-机耦合模拟，研究刹车盘表面温度、应力的变化过程。图3为0.27 s时刹车盘盘面温度场和应力场的分布云图。

图3(a)显示，滑摩过程中，盘面形成了局部的温度环带，高温区域主要分布在摩擦接触位置，非接触位置的温升较为缓慢，盘面最高温度所在的位置与移动热源的位置始终保持一致。观察整个盘面不难看出，周向温度与径向温度变化均形成了明显的温度梯度。图3(b)显示，刹车盘温度场与应力场分布相似，两者存在较强耦合关系。

2.1 温度场分析

分别选取有限元模型中刹车盘沿径向的5个节点，以研究摩擦副温度场随时间变化规律。节点位置涵盖了刹车盘盘面径向中部和内外边缘，如图4所示。

从图4可以看出，盘面节点温度整体呈现出“锯齿状”形式上升。节点3温度相比其他节点较高，最高温度出现在中径位置。在制动初始阶段，沿径向分布的各节点温差较小，随着摩擦热流输入到刹车盘接触表面，接触区域的温度开始升高，且随着时间的增加盘面温度持续上升。摩擦热源主要来自于接触区域，整个摩擦副只存在热传导和热对流的作用，不考虑热辐射。图4中节点温度上升的时间段，节点位于摩擦接触区域内，热传导和热对流为散热的过程，所以此时移动热源的产热量大于刹车盘热传导和热交换作用的散热量。节点温度下降的时间段，节点位于非接触区域内，该区域内无热量的生成，只存在热传导和热交换的作用，这两种作用导致盘面热量散失，使得未接触区域的温度有所下降。刹车盘表面的热源位置随着刹车盘的旋转不断改变，盘面温度虽然经历了上升-下降的交替变化过程，但在0.27 s的时刻，盘面各节点温度相较于起初的20 ℃均有所上升。

图5所示为不同时刻刹车盘盘面温度沿半径分布曲线。图中显示，环面径向中部位置相对于环面内外边缘处温度较高，在半径86 mm处温度最高，半径69 mm处温度最低，随着时间的增加，盘面径向最大温差由30 ℃升高到最大值，此时径向温差为62 ℃。环面整体呈现边缘温度低、中间温度高的分布规律，形成明显温度梯度，这是由于在滑摩过程中，热量在热源经过的位置不断积累，中部位置相对于环面内外边缘处不易散热，累积热量最多，温度高于环面内外边缘位置，产生较为明显的温度梯度。如图5所示，从0.09 s到0.18 s相同半径位置的温升为ΔT1，0.18 s到0.27 s为ΔT2，相同时间间隔内，相同半径位置的温升有所减小，这是由于刹车盘转速随着时间的增加有所下降，也即式(1)中的转速差Δω减小，导致热流密度减小，盘面温升随之减小。

2.2 应力场分析

图6所示为刹车盘Mises应力随滑摩时间变化曲线,Mises应力反应了单元整体应力水平。盘面节点应力随时间呈先增大后减小的交替变化规律。节点3的应力值较大，对应盘面的中间位置；节点1和5的应力值较小，对应盘面的内外边缘位置。盘面应力呈现中间位置大、边缘位置小的分布特征，滑摩时间t=0.21 s时应力最大为150 MPa。盘面主要受到由外载荷作用所产生的机械应力以及盘面温差所产生的热应力的作用。

图7所示为不同时刻刹车盘节点应力沿径向分布曲线。

如图所示，应力集中区主要分布于半径86 mm处，不同时刻的径向最大应力差值如表3所示，盘面最大径向应力差值出现在0.27 s这一时刻。有限元模拟为热-机直接耦合，接触面各节点的温度状态非线性分布致使各节点应力状态发生非稳态变化，应力分布的不均匀性又加剧了温度的不均匀性，二者相互作用，对刹车盘的性能产生影响。

表3 不同时刻的最大径向应力差

3 影响因素分析

3.1 压力的影响

有限元模拟过程中设置的边界条件不变，均布压力分别为14 MPa、17 MPa、20 MPa，模拟得到的刹车盘温度场分布如图8所示。

图8(a)所示为半径86 mm处温度随压力增加的瞬时变化规律，在压力较低时，温度上升缓慢，温度梯度较小。滑摩时间不变，压力增大时，温度上升剧烈，增加相同的压力，温升的幅度也基本相同。随着压力的增大，温度梯度也迅速增大，加剧了盘面温度分布不均，促进局部高温区的产生，影响刹车盘摩擦副的正常工作。

从图8(b)可以看出，压力增大使得整个刹车盘接触面温度整体上升。不同压力下刹车盘盘面径向温度均值和最大温差如表4所示，可以看出压力由14 MPa增长到17 MPa的盘面平均温升为24.29 ℃，高于压力由17 MPa增长到20 MPa的平均温升19.01 ℃。但压力由14 MPa增长到17 MPa的盘面径向最大温差为19.6 ℃，低于压力由17 MPa增长到20 MPa的径向最大温差21.81℃。较大的压力更易提升刹车盘的径向温度梯度，产生局部高温区，引发刹车盘损伤和破坏。

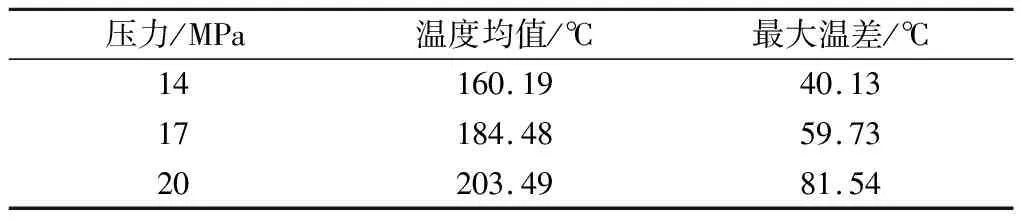
表4 不同压力下的径向温度均值和最大温差

3.2 对流换热系数的影响

在盘式制动器的实际制动过程中，可以通过改善散热条件来加大刹车盘与外部环境的对流换热。通风式刹车盘采用风冷的方式降低刹车盘的温度。由式(6)可知，改变刹车盘周围环境的空气流速，可控制刹车盘表面对流换热系数。不改变摩擦副的边界条件，设置不同的对流换热系数进行仿真，分析对流换热系数对刹车盘温度场的影响。假设正常工况下的对流换热系数α=100 W/(m2·K)。经计算，对流换热系数为α、α/2和2α时对应的空气流速为96.21 m/s、27.28 m/s和166.27 m/s。测量点1、3的温度变化如图9所示。

从图9中可以得出，刹车盘表面节点3处也即径向中部位置温度值较高。但盘面同一位置在不同的对流换热条件下，温度的变化范围不超过2%，说明对流换热系数对盘面温度总体变化趋势基本没有影响。增大盘面对流换热系数，盘面温度略有降低，但降低幅度较小，盘面径向边缘位置的温升变化比中部位置稍大。总体上对流换热系数对刹车盘温度场的分布及温度随时间变化情况影响较小。

若使用水冷的方式改变盘面对流换热系数，使摩擦副接触面间有液态水流过，不考虑水的热传导及热吸收，则摩擦副接触面对流换热可看作水横掠圆柱体的对流换热[15]，换热系数为

(8)

式中:ν为接触面上某点的线速度；d为接触面的半径；γ为运动黏度；Pr为普朗特数；m2、n为经验系数，分别取值为0.193、0.618[16]。

表5为液态水的物理参数，将其代入式(8),得出水冷的对流换热系数与刹车盘转速的变化曲线，如图10所示。从图中可以看出，水冷方式下，提高刹车盘的转速，可获得较大的对流换热系数，实现盘面良好的散热条件。

表5 液态水物理参数(20℃)

不改变其他条件，采用水冷的方式进行模拟，得到如图11所示的温度变化曲线。水冷方式下盘面节点3和节点1的最高温度分别为170.729 ℃和119.091 ℃，比风冷方式下的节点3和节点1的最高温度略有降低。

刹车盘盘面节点1和3在水冷和风冷条件下的温差随时间的变化曲线如图12所示。水冷条件下的盘面温度为Tw，风冷条件下的盘面温度为Td，图中曲线的纵坐标为Td-Tw。从图中可以看出，水冷条件下的盘面温度较风冷有所降低，下降幅度最高达到15 ℃。对于刹车盘摩擦副，水冷的方式相较于风冷不仅更易控制，而且还可以取得相对较好的冷却效果。

4 结束语

本文基于ABAQUS对刹车盘的滑摩过程进行有限元模拟，构建了刹车盘温度场的有限元模型，探究了制动压力和对流换热系数对于盘面温度的影响规律，并对水冷和风冷的冷却效果进行了比较。研究结果表明，刹车盘在滑摩过程中，盘面节点温度随时间呈现出“锯齿状”形式上升，盘面径向中部位置的温度高于边缘位置，形成明显的温度梯度。刹车盘温度值和温度梯度随着接触面压力的增大而增大；对流换热系数增大时，刹车盘温度值减小，刹车盘采用水冷的冷却效果优于风冷。以上针对有限元模拟结果所得出的结论，对于刹车盘的性能提升具有参考价值，但还需要一定的试验数据进行验证。如果能深入探究刹车盘盘面温度场对其摩擦性能的作用机理，提出可行的降低盘面温度的有效措施，将有助于提升刹车盘的工作性能。