时间加权非局部反应扩散方程解的性质 ①

余巧云, 孟海霞

(兰州交通大学数理学院，甘肃 兰州 730070)

0 引 言

研究具有时间加权系数的非局部扩散方程

(1)

(2)

解的局部存在性和唯一性，采用Bananch不动点定理分别得到了Cauchy，Dirichlet 和Neumann初边值问题下解的局部存在性和唯一性.

在扩散问题的研究中，一类带有时间加权系数的扩散作为描述扩散现象的新模型，具有一定的实际的意义，引起了国内外许多学者的关注. 其中经典的局部(拉普拉斯算子Δu作为扩散算子)扩散问题可参阅文献[7-10]及其参考文献. 特别地，在文献[7-8]中Payne和Philippin研究了下列典型的具有时间加权系数的半线性抛物型方程

(3)

分别在Neumann边界条件与Dirichlet边界条件下解的情况. 在对反应项做出某些适当的假设条件下，通过微分不等式的技巧，证明了解的存在性与爆破性，得到了爆破时间的上下界.在文献[9]中Ahmed研究了下列反应项为非局部的具有时间加权系数的扩散问题

(4)

解的性质，获得了解全局存在及其发生爆破时的充分条件，还得到了爆破时间的上界. 再如2017年Marras和Vernier在文献[10]研究了反应项与边界条件下均有时间加权系数的扩散方程

(5)

解的爆破时间的上下界. 自此之后就有大量的文献研究此类方程及其变形式. 然而，对于具有时间加权系数的这种非局部(以卷积算子J*u-u作为扩散算子)扩散问题的研究就比较少. 如Zhang于2011年在文献[11]研究了在Dirichlet边界条件下带有反应项的非局部扩散方程

(6)

(7)

解的全局存在性. 利用Banach不动点定理证明了方程组解的局部存在性和唯一性，通过建立比较原理，得到一定条件下方程组解的全局存在性.

受上述文献的启发，考虑到非局部扩散具有研究范围广和一定的理论基础，实际意义也更为丰富的优点，本文研究了一类带有时间加权系数非局部反应源项的非局部扩散方程(1)在Dirichlet边界条件下解的局部存在性与爆破性. 既不同于上述[7-10]中的局部扩散，也不同于[11-12]中将时间加权系数具体化，本文讨论了一类范围更广，更具代表性的含有时间加权系数非局部反应源项的非局部扩散方程. 首先，通过引理1的证明及其结合Banach不动点理论验证了解的局部存在性定理. 其次，通过构造一个新的指数型辅助函数及其运用微分不等式技巧，求得了解爆破的充分条件，并且得到了爆破时间的上界估计. 主要的困难是寻找带有时间加权系数k(t)的反应源项对爆破解的影响及其证明爆破定理时辅助函数的构造. 通过对问题(1)解的相关性质的研究，发现无论是解的存在性还是爆破性均受到了非局部反应源项的时间加权系数k(t)与非局部区域体积|Ω|的影响. 结构安排为第二部分研究解的局部存在性，通过引理1的证明及其结合Banach不动点定理验证了解的局部存在性. 第三部分研究解的爆破性质，给出非局部算子在Dirichlet边界条件下的特征值与特征函数，结合时间加权系数k(t)构造了新的指数性辅助函数，运用微分不等式的技巧，最终得到发生爆破时的充分条件与爆破时间的上界估计.

1 解的局部存在性

这部分通过Banach不动点理论研究问题(1)解的局部存在性.

先给出一些必要的准备.

赋予范数

易知Xt0是Banach空间，令

且B(0,R)⊆Xt0，记映射

则问题(1)的解u(x,t)将由算子Tu0(u)(x,t)的不动点得到，现引出以下引理:

进一步，当t0足够小时，Tw0(w)(x,t)在球B(0,R)中是严格压缩的.

|Tw0(w)(x,t1)-Tw0(w)(x,t2)|=

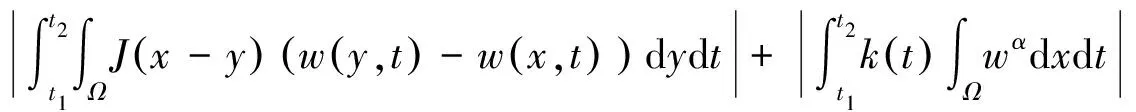
“北接松径，南通峦雉，东以达虎角庵。游者之屦常满，然而素桷茅榱，了不异人意。”[3]426此亭构造简朴，一点也不吸引游者的眼球。然而登亭眺望，胜景扑面而来，使人油然而生山水鱼鸟之情。

k(t0)αRα-1|Ω|)‖w-z‖Xt0t,

得Tw0(w)(x,t)在球B(0,R)中是严格压缩的.

证明由Banach不动点理论及其引理1，可以得到问题(1)在[0,t0]上存在唯一解.

2 解爆破的充分条件

这部分讨论解的爆破性.为了估计爆破时间，首先引入关于非局部扩散问题的特征值引理，参阅文献[13-14].

引理2设非局部算子的Dirichlet特征值问题为

(5)

其中Ω是RN中的有界光滑区域. 则上述问题存在一个特征值λ1(Ω)与相应的特征函数φ1(Ω)，并且特征值λ1(Ω)是唯一的，且满足0<λ1(Ω)<1，而且该特征值可以表示成

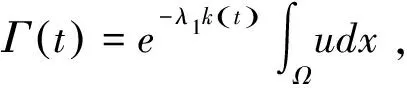
由Schwarz不等式可得

则上式

Γ′(t)≥-λ1k′(t)Γ(t)-λ1Γ(t)+

k(t)|Ω|eλ1(α-1)k(t)Γα(t),

进一步地由假设条件可得

Γ′(t)≥-λ1σκΓ(t)-λ1Γ(t)+

κ|Ω|eλ1(α-1)k(t)Γα(t)≥

-λ1(1+σκ)Γ(t)+κ|Ω|Γα(t),

解上面微分方程可得

则当初值足够大，且满足

时，Γ在有限时间内爆破，且