基于电容等效阻抗高频特性的滤波方法研究

摘  要：文章提出了一种以电容阻抗高频特性为基础的串扰耦合干扰的滤波抑制方法。介绍了实际情况中电容的等效阻抗在高频工作条件下所表现出的特性，分析了电容滤波时的工作原理。电容滤波的本质是在信号传输通道与“地”之间搭建一条针对干扰信号的低阻抗通道，使干扰信号在进入敏感工作电路之前就通过低阻通道被泄入“地”中，进而达到滤除干扰的目的。利用电容这一特性，成功实现了对干扰信号的有效滤除，并通过仿真验证了其可行性。

关键词：电容;等效阻抗;高频特性;滤波

中图分类号：TM13   文献标识码：A文章编号：2096-4706（2021）14-0062-06

Abstract： This paper proposes a filtering method of crosstalk coupling interference based on the high frequency characteristic of capacitive impedance， introduces the characteristics of the equivalent impedance of the capacitor in the high frequency working condition， and analyzes the working principle of the capacitor filter. The essence of capacitance filtering is to build a low impedance channel between the signal transmission channel and the “ground” for interference signal， so that the interference signal is discharged into the “ground” through the low impedance channel before entering the sensitive working circuit， so as to achieve the purpose of filtering interference. Using the characteristic of capacitance， the interference signal is filtered effectively， and the feasibility is verified by simulation.

Keywords： capacitance; equivalent impedance; high frequency characteristics; wave filtering

0  引  言

当前最主要的电磁干扰抑制方法有屏蔽、接地和滤波，其中滤波又是可使用范围最广，可研究领域最深，可实现目标最明确的一种方法。滤波实际上就是把信号分成需要用到的工作分量和不希望有的干扰分量，然后通过合理设计滤波结构，在传输线路与“地”之间为干扰分量提供一条低阻抗通道，进而达到将干扰滤除的效果。随着各式各样的电子设备越来越趋向于高集成度、高精度、小型化、高速化，传统的相对大型的滤波器结构已无法满足电路设计要求，器件滤波成为滤波设计中的热门。可用于滤波的器件包括电容、电感、电阻以及铁氧体磁珠等，其中电容是最典型、最常用的旁路滤波器件。当前滤波结构中对电容的选取多是定性的根据设计师的判断和经验，没有严密定量的分析计算的过程，随着工作电路工作频率的升高，时常会出现选用的电容不能很好达到滤波目的，甚至会严重影响工作信号的现象。为此，本文严谨地利用了电容等效阻抗的高频特性，通过定量计算的方法为需要滤波的电路选取最佳电容值，为滤波电容的选取提供了理论及计算依据，并实现了在工作信号尽可能不受影响的前提下，对干扰信号进行有效的滤除，提高了电容滤波措施的严谨性及可靠性。

1  基于电容等效阻抗高頻特性的滤波原理

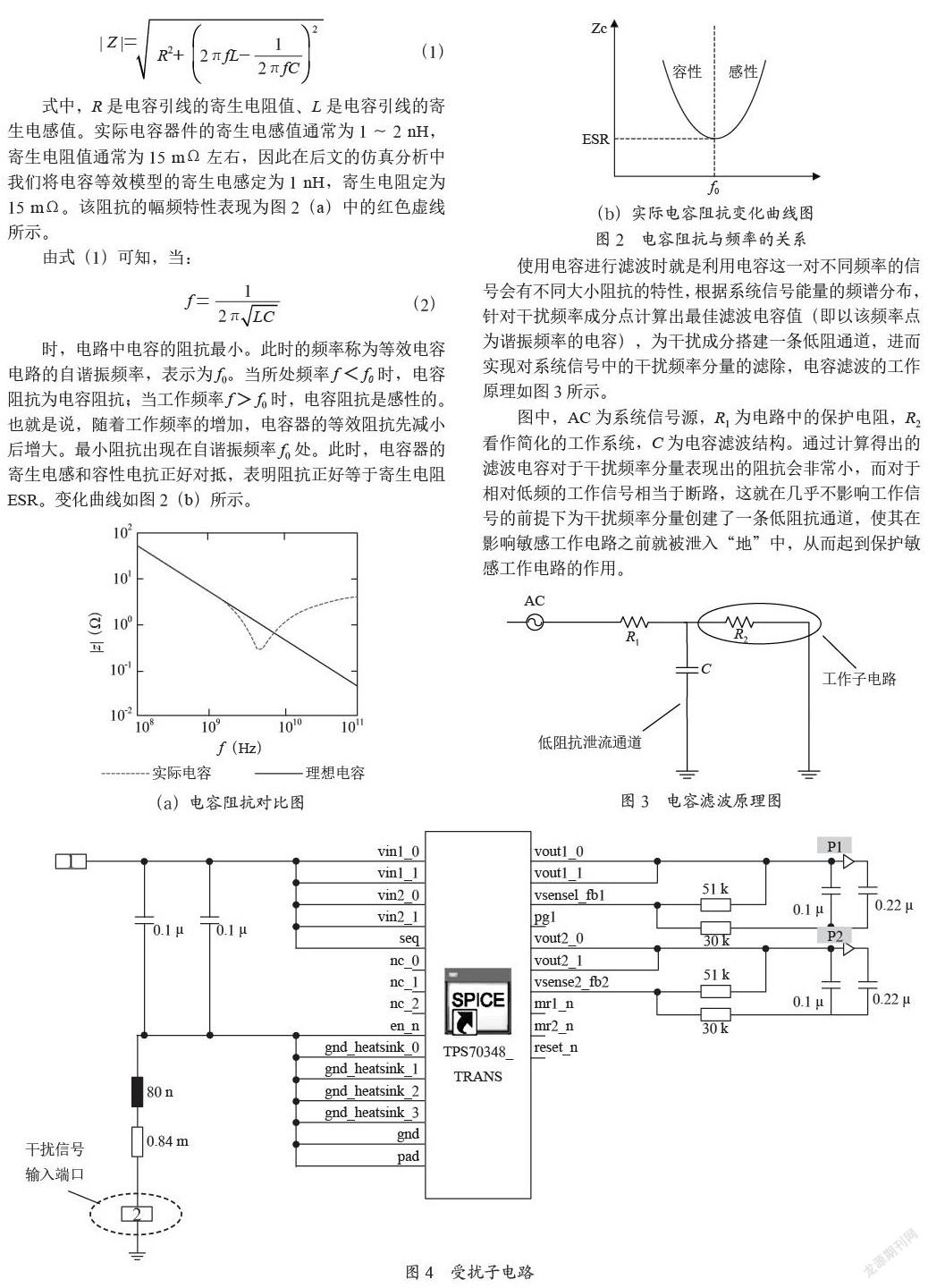
理想情况下的电容，其寄生的电阻和电感都是可以忽略不计的，其阻抗为| Z |=1/（2πfC），即随着工作频率的增高、电容值的增大，电容的阻抗就变得越小。此时在设计针对高频干扰的滤波电容时不存在任何顾虑，电容值越大，滤波效果就越好。但实际情况有所不同，由于电容引脚及连接线的存在，其本身也存在着寄生的电感和电阻，且在高频时会对系统造成较大干扰，这时候不再是电容越大越好，而是需要计算合适的电容值。

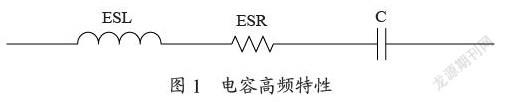
高频工作条件下，电容器件可以被等效成为一个由电容、电阻和电感组成的简化串联电路，如图1所示，此时可以用该串联的谐振电路表示电容。

时，电路中电容的阻抗最小。此时的频率称为等效电容电路的自谐振频率，表示为f0。当所处频率ff0时，电容阻抗是感性的。也就是说，随着工作频率的增加，电容器的等效阻抗先减小后增大。最小阻抗出现在自谐振频率f0处。此时，电容器的寄生电感和容性电抗正好对抵，表明阻抗正好等于寄生电阻ESR。变化曲线如图2（b）所示。

使用电容进行滤波时就是利用电容这一对不同频率的信号会有不同大小阻抗的特性，根据系统信号能量的频谱分布，针对干扰频率成分点计算出最佳滤波电容值（即以该频率点为谐振频率的电容），为干扰成分搭建一条低阻通道，进而实现对系统信号中的干扰频率分量的滤除，电容滤波的工作原理如图3所示。

图中，AC为系统信号源，R1为电路中的保护电阻，R2看作简化的工作系统，C为电容滤波结构。通过计算得出的滤波电容对于干扰频率分量表现出的阻抗会非常小，而对于相对低频的工作信号相当于断路，这就在几乎不影响工作信号的前提下为干扰频率分量创建了一条低阻抗通道，使其在影响敏感工作电路之前就被泄入“地”中，从而起到保护敏感工作电路的作用。

2  电容滤波的应用与验证

2.1  滤波对象介绍

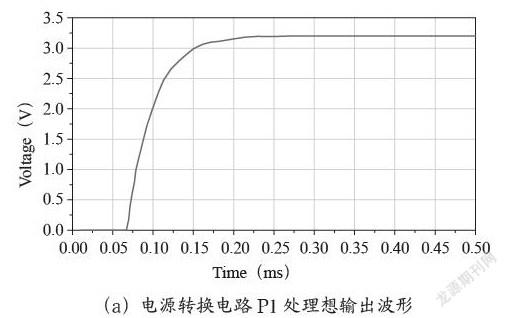
本文研究的滤波对象为一个5 V—3.3 V/1.5 V的电源转换电路，如图4所示。电路工作时，外部电源能够提供5 V的直流电压，而系统不需要如此高的电压进行供电，所以需要对电压进行转换。如果电压转换发生错误，则后面所有的电路都将无法实现其预期功能。在所研究的系统中，线间串扰通过地线耦合进入电源转换电路，对系统输出信号产生很大影响。为便于分析简化文章，在受扰子电路的接地处增加一个外部输入端口2来代替产生干扰的复杂电子系统，外部端口2所输入的信号即为提取的线间串扰信号。本文通过用外部输入端口代替复杂电子系统的方式可精确实现系统传输信号的重现且简化了模型，提高了效率。

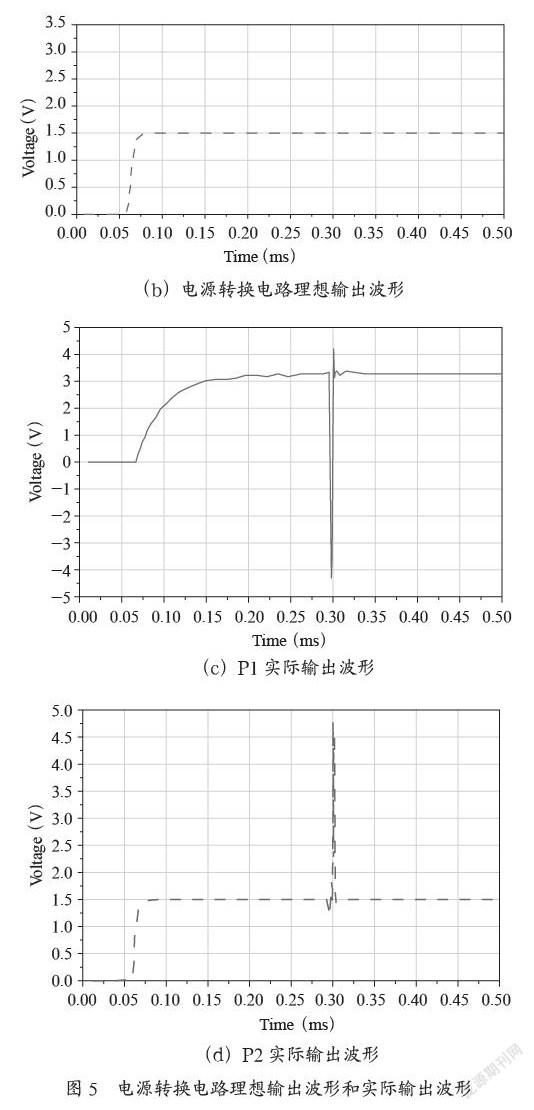
该电源转换电路在未受干扰时的P1、P2点处的输出波形如图5（a）、图5（b）所示，而实际输出波形如图5（c）、图5（d）所示。可以看出，在0.3 ms时，电路受到了干扰，芯片输出信号发生了波动。若该波动最大幅值超过了器件工作阈值，则会被烧毁。为了保证工作系统正常运行，需要对该干扰进行抑制。

2.2  干扰信号分析及电容值的选取

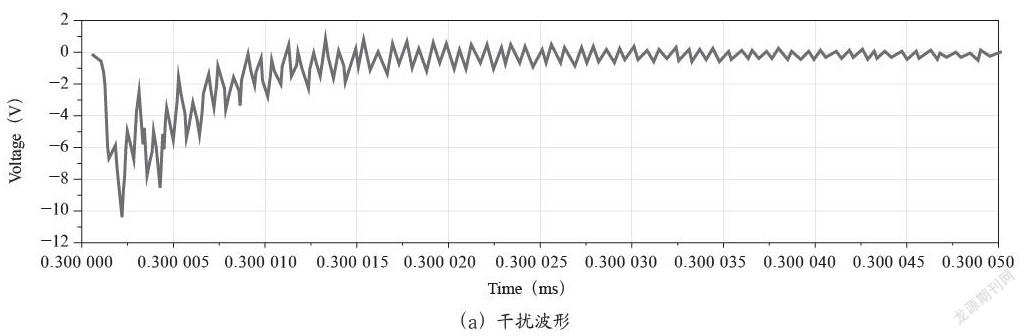
由电容滤波机理可以知道，要想实现滤波电容的精确最佳取值，首先要明确干扰信号的频率分布，然后再以干扰中的能量分布集中频率点作为待选电容的谐振频率f0，经由串联谐振反推公式C=1/4π2Lf02计算出最佳滤波电容值，以为想要滤除的干扰分量搭建一条低阻抗通道。提取的干扰信号在0.3 ms附近的时域波形如图6（a）所示，对提取出的无用信号进行时频域变换，得到如图6（b）所示的频谱图。

分析干扰信号的频谱图可知，串扰干扰的能量集中分布于以625 kHz、0.48 GHz以及1.3 GHz为中心的三个频点附近。基于这三个能量集中频点，通过公式C=1/4π2Lf02对最佳滤波电容值进行计算可得：当f0=1.3 GHz时C=15 pF;当f0=0.48 GHz时C=0.11 nF;当f0=625 kHz时C=64.84 μF。

2.3  电容滤波效果验证

2.3.1  15 pF电容滤波效果验证

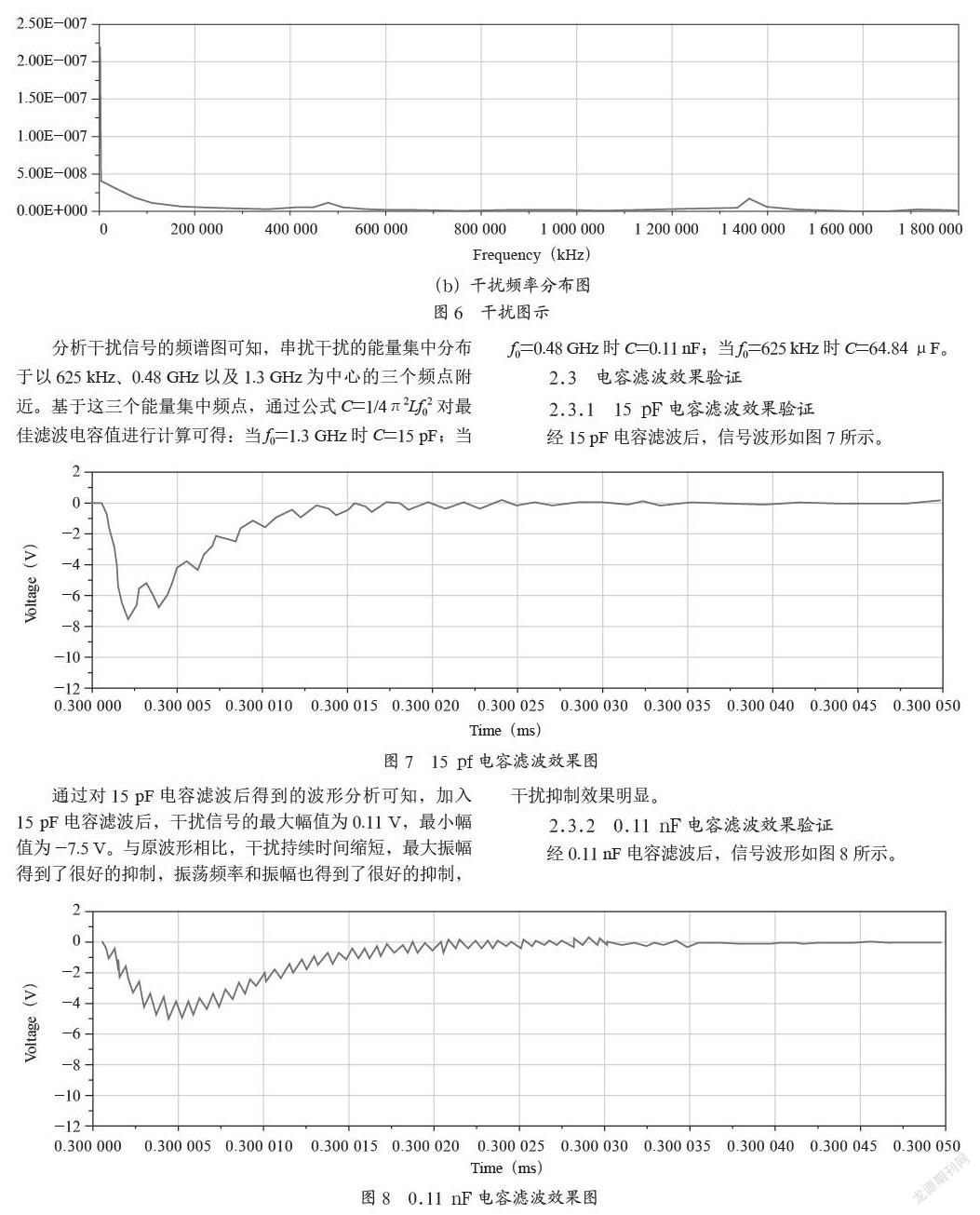
经15 pF电容滤波后，信号波形如图7所示。

通过对15 pF电容滤波后得到的波形分析可知，加入15 pF电容滤波后，干扰信号的最大幅值为0.11 V，最小幅值为-7.5 V。与原波形相比，干扰持续时间缩短，最大振幅得到了很好的抑制，振荡频率和振幅也得到了很好的抑制，干扰抑制效果明显。

2.3.2  0.11 nF电容滤波效果验证

经0.11 nF电容滤波后，信号波形如图8所示。

通过对0.11 nF电容滤波后的波形分析可知，加入0.11 nF电容滤波后，干扰信号的最大幅值为0.12 V，最小幅值为-4.87 V。与原波形相比，干扰持续时间更短，最大振幅也得到了很好的抑制，最小振幅也得到了一定程度的有效抑制，但振荡频率变化不大，振荡幅度仍有所减小，对干扰信号有一定的滤波作用。

2.3.3  64.84 μF电容滤波效果验证

经64.84 μF电容滤波后，信号波形如图9所示。

通过对64.84 μF电容滤波后的波形分析可知，加上64.84 μF电容滤波后，干扰信号的最大幅值为0.89 V，最小幅值为-0.87 V。与原始波形相比，干扰持续时间缩短，最大振幅变化不大，最小振幅受到明显抑制，振荡频率几乎不变，振荡幅度明显减小，滤波效果明显。

在滤除干扰时，需要参考两个指标：干扰幅度和干扰频率（信号稳定性）。根据图4受扰子电路中干扰信号的时频特性和滤波要求可知，15 pF和64.84 μF大小电容并联滤波是对系统干扰信号进行滤波的最有效的方法：64.84 μF大电容用于抑制干扰对电路的影响幅度（最小幅度）;15 pF小电容用来调节扰动的振荡频率（电路稳定性），滤波电路模型如图10所示。

经64.84 μF和15 pF两电容并联进行滤波后，受扰子电路中P1处的输出波形如图11所示。

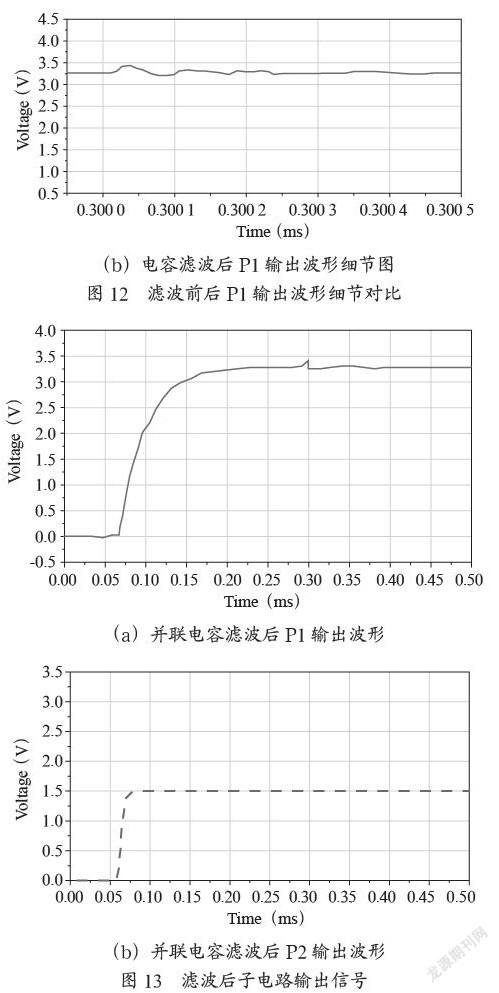
滤波前后P1输出波形细节对比图如图12所示。

由并联电容滤波结果图可知，并联电容结构为干扰信号中大部分频率成分提供了一个低阻抗通道，干扰信号中的能量大都通过电容直接泄入大地，因此耦合进入工作系统的干扰信号的电压幅值和频率大大地被削减了。图13为并联电容滤波后子电路P1、P2点处的输出信号，可见在0.3 ms处发生的干扰已得到了很好的控制，且正常工作信号几乎没有受到影响，验证了该措施的有效性、可行性。

3  结  论

本文首先对提取的干扰信号进行了傅立叶变换得到其频谱图，分析其频谱图可知干扰成分的能量集中分布于以625 kHz、0.48 GHz以及1.3 GHz为中心的三个频点附近;然后将电容等效阻抗的高频特性及其滤波原理相结合计算出了当以这三个频点作为待选滤波电容的自谐振频率时所对应的最佳电容值为64.84 μF、0.11 nF和15 pF;接着分别采用三种值的电容设计滤波结构，进行干扰信号的滤除，发现经值为15 pF的电容进行滤波后，信号的波动频率得到了良好的抑制;经值为64.84 μF的电容实现滤波后，串扰信号整体实现了很好的抑制。最终得出可设计15 pF和64.84 μF一小一大两个电容并联滤波的结构对干扰进行有效滤除和抑制的结论，仿真实验表明，该方法滤波效果良好，对有用工作信号几乎没有影响，可靠性高。

参考文献：

[1] 杨克俊.电磁兼容原理与设计技术 [M].北京：人民邮电出版社，2004.

[2] 蔡荭，邹学峰，罗旸，等.浅析旁路电容的特性及其在PCB中的应用 [J].电子与封装，2010，10（7）：35-39.

[3]SHI R S，DARCHERIF A，SABONNADIERE J C. Computation of transient electromagnetic fields radiated by a transmission line：An exact model [J].IEEE Transactions on Magnetics，1995，31（4）：2423-2431.

[4] PAUL C R，BUSH D R. A comparison of the contribution of common-mode and differential-mode currents in radiated emissions [J].IEEE Transactions on Magnetics，1989，31（2）：189-193.

[5] CROSS P C. Elementary matrix algebra [M].London：Macmillan，1973：16-20.

[6] CHEN B C. Linear System Theory and Design [M].New York：McGraw-Hill，2012：20-32.

[7] RALSTON A. A first course in numerical analysis [M].New York：McGraw-Hill，1978：47-53.

作者簡介：谭超（1979—），男，汉族，山东安丘人，高级工程师，学士学位，研究方向：集成电路设计。