基于FFT的仅相位加权阵列天线波束赋形优化方法

王辰 邱明华 柏业超 陈妍

摘  要：为了解决仅相位加权的天线波束赋形问题，文章提出一种基于快速傅立叶变换的方向图综合算法。在仅相位加权的约束条件下，應用一维傅立叶逆变换获得方向图并与期望方向图进行对比，将方向图进行调整后再使用快速傅立叶变换获得阵元对应的幅相激励，并对阵元中的幅度激励进行约束。结果显示，该相位加权的工作形式，可有效降低系统中馈电网络的复杂度。

关键词：仅相位加权;可重构天线;波束赋形;快速傅立叶变换

中图分类号：TN820     文献标识码：A文章编号：2096-4706（2021）14-0046-03

Abstract： In order to solve the problem of antenna beam forming with only phase weighting， a pattern synthesis algorithm based on fast Fourier transform is proposed in this paper. Under the constraint of only phase weighting， the pattern is obtained by one-dimensional inverse Fourier transform and compared with the expected pattern. After adjusting the pattern， the amplitude and phase excitation corresponding to the array element is obtained by fast Fourier transform， and the amplitude excitation in the array element is constrained. The results show that the phase weighted working form can effectively reduce the complexity of the feed network in the system.

Keywords： phase-only control; reconfigurable antenna; beam forming; fast Fourier transform

0  引  言

雷达技术的发展对天线阵列各项性能数据指标的要求越来越高，而有源相控阵天线的出现对满足这些性能指标提供了巨大的潜力，它已经广泛应用于各个雷达领域，如地面军工战略雷达，舰载雷达、机载预警雷达，星载雷达等。而天线阵列的方向图综合问题，是天线设计研究中一个极为重要的研究方向。近四十年来，国内外学者提出了很多方法[1-3]。

迭代傅立叶算法出自1980年代发明的雷达天线校对方法[4]，其数学依据是一种交替投影方法[5]。在均匀阵列中，单元等间距分布，间距均为半波长，由于远场方向图与单元激励之间存在快速傅立叶（Fast fourier transform，FFT）变换关系，算法中利用FFT及其逆变换（Invert fast fourier transform，IFFT）循环，该方法极大缩短阵列综合所需的时间。这一成果被广泛应用于阵列综合相关研究领域，相关内容如2007年文献[6]中，Keizer将FFT应用于超大型阵列（阵元个数超过5 000个）综合研究中，在5%的阵元随机损耗后，FFT可以对方向图进行有效且快速的调整，与文献中的其他方法相比，迭代傅立叶算法调整后的副瓣降低了约5 dB，同一作者在后续文献中阐述了FFT方法及其改进形式在平面阵综合、大型稀疏阵方面以及单脉冲天线和差波束方向图综合研究中的相关成果，可以有效降低系统中馈电网络的复杂度，如文献[4]，随文开源了相关技术的MATLAB代码。2011年，该作者利用FFT方法在阵列综合中对单元的幅相进行了离散化操作，从而有益于阵列在实际应用中实现[7]。在此基础上，2012，Keizer再次利用FFT方法[8]对阵列综合中的单元激励进行锥削化处理，在实现激励幅度的连续分布的同时还提高了方向图辐射性能。后续研究中，该作者将随机密度锥削技术与迭代傅立叶算法相融合，对多种波束形式进行稀疏化处理，并提高方向图辐射性能[9]。

为了解决仅相位加权（Phase-Only Control）的波束赋形形式，本文提出了一种基于快速傅立叶变换的方向图综合算法。在仅相位加权前提条件下，将阵列中初始单元激励均设为1，应用IFFT变换计算远场方向图，并与期望方向图进行对比，将方向图进行调整后再使用快速傅立叶变换获得阵元的激励，再对激励的幅度值进行均值约束。循环操作，直到方向图符合设计的性能参数要求。

1  远场方向图模型

为描述仅相位加权的天线波束赋形问题，本节假设一个直线阵，单元总数设为M，阵元间距均设为d，则阵列的远场方向图表达式可表示为：

式（4）中，采样间隔w0为2π/N，周期为k=0，1，2，…，N-1，N，对比式（4）与式（2）内容，这里得到Am（阵元激励）与AF（阵列因子）存在傅立叶变换关系。这里的AF可由对阵元激励做一维离散傅立叶逆变换再乘以周期得到，这里的样本采集数为N。

在反复循环过程中，需要重复的计算式（2），在计算（3）式时，均需要进行操作M次相乘和M-1次相加处理。这里假设有K个采样点，为保证方向图的精准性，K值的选择必须远大于M（阵列中单元数），在这一过程中，则需要操作K×M次相乘和K×（M-1）次相加，值得注意的是，K×M值与乘法次数和加法次数均有关，K值增大，则计算负担急剧增加。而当使用阵因子与阵元激励之间的傅立叶变换来获得方向图时，计算负担（只和KLog2K成正比）则明显减少，可以明显缩短计算时间，提高计算效率增减算法应用的实时性。

在本节提出的FFT方法应用中，所有阵元的激励初始值均为1，实现仅相位加权天线波束赋形的具体步骤为：

（1）假设数组{AiK}，数组大小設置为K，个数为i（波形数量i =1，2，…，i），该数组由{AiM}补零产生，由（2）式计算获得阵因子{AFiK}。

（2）对获得的阵因子做归一化操作，相位值ΨiK与激励值|AFiK|由此获得。

（3）区分|AFk|中主瓣区域和副瓣区域。对副瓣区域中高出约束电平的点，一律变成预设最大副瓣电平，将主瓣|AFk|的值与期望阵因子进行匹配，如主瓣中超出预设波纹上下边界的点，本节用上下边界来替换。

（4）若循环迭代的次数达到设定的最大值或主、副瓣区域超过阈值的点为零则循环截止，否则进入5步骤。

（5）获得AFiKNew=|AFiK|Newexp（jΨiK），其中幅度为|AFiK|New，ΨiK为第二步中结果。

（6）获得{AiiK}，这里利用了FFT变换对AFiKNew进行处理，阵元激励{AiK}由前M个值获得。|Am|=（|A1m|+ |A2m|+，…，Aim）/i为激励取均值处理。

（7）重复循环步骤1。

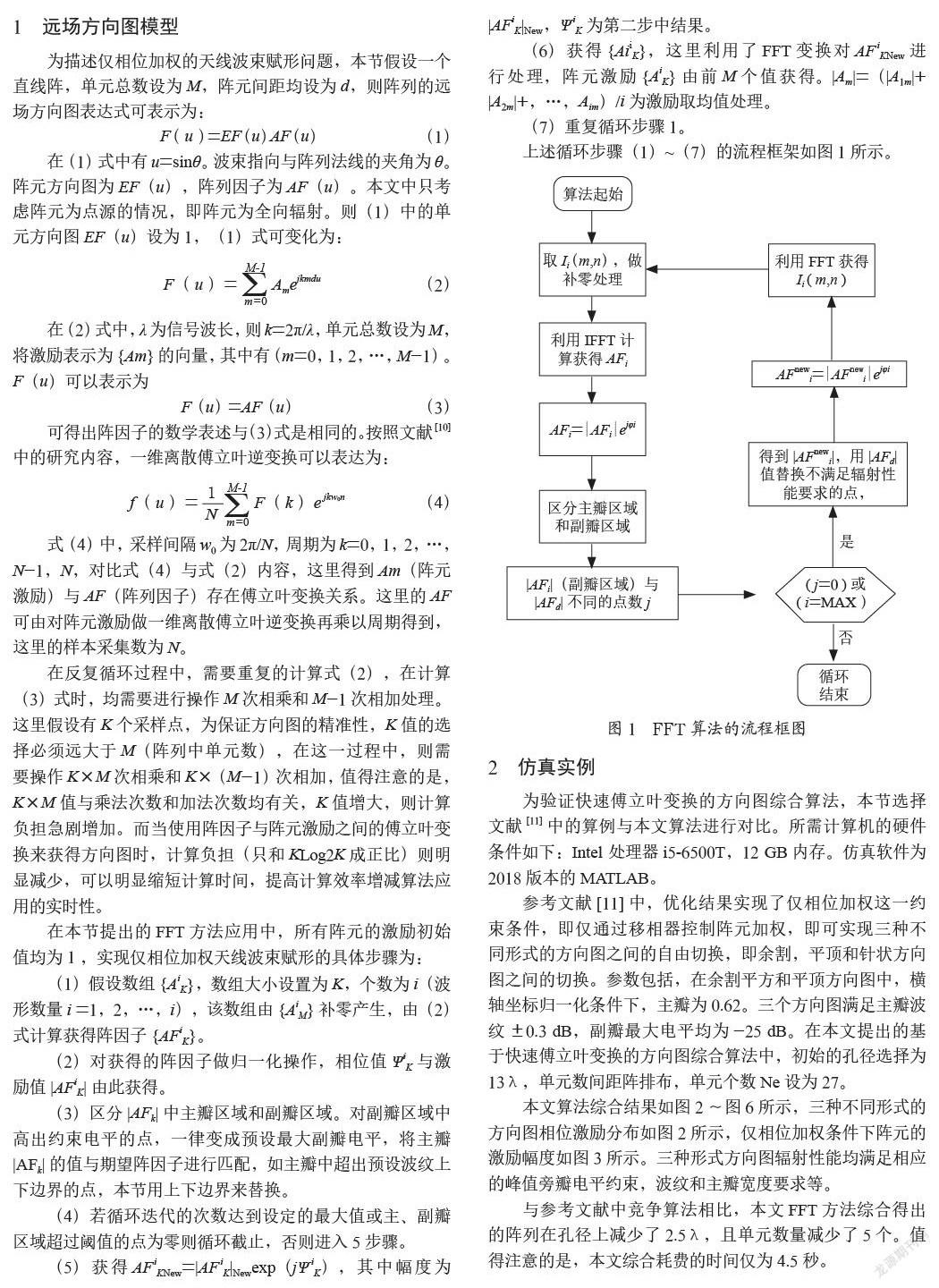
上述循环步骤（1）～（7）的流程框架如图1所示。

2  仿真实例

为验证快速傅立叶变换的方向图综合算法，本节选择文献[11]中的算例与本文算法进行对比。所需计算机的硬件条件如下：Intel 处理器i5-6500T，12 GB内存。仿真软件为2018版本的MATLAB。

参考文献[11]中，优化结果实现了仅相位加权这一约束条件，即仅通过移相器控制阵元加权，即可实现三种不同形式的方向图之间的自由切换，即余割，平顶和针状方向图之间的切换。参数包括，在余割平方和平顶方向图中，横轴坐标归一化条件下，主瓣为0.62。三个方向图满足主瓣波纹±0.3 dB，副瓣最大电平均为-25 dB。在本文提出的基于快速傅立叶变换的方向图综合算法中，初始的孔径选择为13λ，单元数间距阵排布，单元个数Ne设为27。

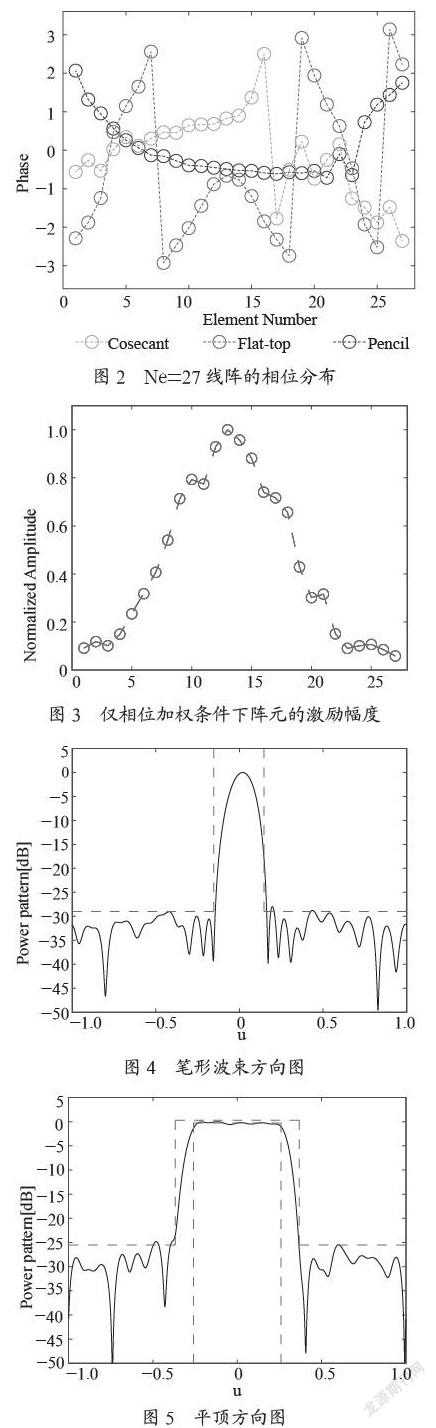
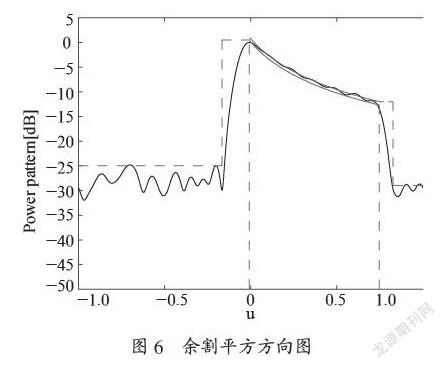
本文算法综合结果如图2～图6所示，三种不同形式的方向图相位激励分布如图2所示，仅相位加权条件下阵元的激励幅度如图3所示。三种形式方向图辐射性能均满足相应的峰值旁瓣电平约束，波纹和主瓣宽度要求等。

与参考文献中竞争算法相比，本文FFT方法综合得出的阵列在孔径上减少了2.5λ，且单元数量减少了5个。值得注意的是，本文综合耗费的时间仅为4.5秒。

3  结  论

阵列天线的多波束方向图综合问题是雷达研究领域中一个极为重要的研究方向。本文提出了一种方向图综合算法，本文提出的仅相位加权的工作形式，可有效降低系统中馈电网络的复杂度，从而有助于天线在实际应用中的实现。此外，本文算法在实时性上具有一定优势。

参考文献：

[1] 祁峥东，邱明华，蒋莹莹，等.基于凸优化理论的和、差波束方向图合成新方法 [J].雷达与对抗，2020，40（4）：41-46.

[2] 孔玥，邱明华，黄晟，等.基于凸优化理论的可扫描稀疏阵列综合 [J].雷达与对抗，2020，40（3）：33-37.

[3] 祁峥东，卢阳沂，孔玥，等.基于多凸优化的稀疏线性阵列综合方法 [J].雷达与对抗，2019，39（4）：21-24+49.

[4] KEIZER W P M. Low-Sidelobe Pattern Synthesis Using Iterative Fourier Techniques Coded in MATLAB [EM Programmer's Notebook] [J]. IEEE Antennas and Propagation Magazine，2009，51（2）：137-150.

[5] BUCCI O M，ELIA G D，MAZZARELLA G，et al. Antenna pattern synthesis：a new general approach [J].Proceedings of the IEEE，1994，82（3）：358-371.

[6] KEIZER W P M. Fast Low-Sidelobe Synthesis for Large Planar Array Antennas Utilizing Successive Fast Fourier Transforms of the Array Factor [J].IEEE Transactions on Antennas and Propagation，2007，55（3）：715-722.

[7] KEIZER W P M. Low Sidelobe Phased Array Pattern Synthesis With Compensation for Errors Due to Quantized Tapering [J].IEEE Transactions on Antennas and Propagation，2011，59（12）：4520-4524.

[8] KEIZER W P M. Amplitude-Only Low Sidelobe Synthesis for Large Thinned Circular Array Antennas [J].IEEE Transactions on Antennas and Propagation，2012，60，（2）：1157-1161.

[9] KEIZER W P M. Synthesis of Thinned Planar Circular and Square Arrays Using Density Tapering [J].IEEE Transactions on Antennas and Propagation，2014，62（4）：1555-1563.

[10] 石力，邓云凯，孙慧峰. 基于FFT的大型平面阵列方向图的综合方法[J].系统工程与电子技术，2011，33（11）：2377-2381.

[11] BUCCI O M，MAZZARELLA G，PANARIELLO G. Reconfigurable arrays by phase-only control [J].IEEE Transactions on Antennas and Propagation，1991（39）：919-925.

作者简介：王辰（1988.02—），男，汉族，辽宁抚顺人，讲师，硕士，研究方向：人工智能与移动信息化。