基于可靠度理论计算重力扶壁式码头结构稳定性
——以泰州内河港7B码头工程为例
2021-01-14陶源
陶 源
(中设设计集团股份有限公司,江苏 南京 210014)
1 前 言
重力扶壁式码头具有自重荷载大、结构稳定、容易施工和检修、取材简单、对冰冻等不利工况适应能力强等优点,被广泛应用于内河航运中。据统计,2010~2016年中,重力扶壁式码头占全江苏新建码头调查样本的比例高达37.3%,是目前最常见的内河码头结构型式之一。
重力扶壁式码头的缺点也同样明显,即对抗滑、抗倾覆能力相对较差。据不完全统计,笔者搜集到的311起重力式扶壁码头失事样本中,因码头滑移、倾覆导致失事的比例高达55.3%。因此,在码头设计阶段就重视抗滑、抗倾覆能力,并针对性地制定相应的对策措施,对于重力式码头的发展和应用具有重要意义。
在《重力式码头设计与施工规范》(JTS 167-2-2018)的附录D中,提出了可靠度指标的概念,并提出了基于可靠度指标进行码头结构稳定性验算的新方法。针对这一新方法提出时间较短,概念尚未普及且未广泛应用,本文拟将这一概念理论引用至重力扶壁式码头结构计算中,首先详细分析可靠度指标的概念及定义,然后以泰州内河港7B码头工程为实例,详细介绍基于可靠度理论计算重力扶壁式码头结构稳定性的具体方法。
2 可靠度指标的概念与定义
将概率论的理念引入至构筑物的结构稳定计算中来,码头在复杂环境条件ζ下,在时间t内维持稳定运行的概率表达定义式如下。
R(t)=f(t,ζ)
(1)
将所有作用在码头结构上的荷载简单地分为承载力fc和荷载效应S,因此,显然可知,码头结构失效的表达式即承载力小于荷载效应的概率,表达式如下:
(2)
式中,ffc(f)为码头结构承载力fc的概率密度函数;fs(S)为码头结构所受的荷载效应S的概率密度函数。Z为码头结构功能状态的函数,表达式如下:
Z=g(fc,S)=fc-S
(3)
假设fc与S均服从正态分布,则根据数理统计的基本概念,可以根据式(3)分别求得码头结构的功能状态Z的平均值与标准差:
μz=μfc-μs
(4)
(5)
因此,根据正态分布函数的几何关系,可将式(2)中的失效概率转换为以下情况:
Pf=P(Z<0)=Fz(0)=
(6)
根据《重力式码头设计与施工规范》(JTS 167-2-2018)对可靠度物理量的定义,表达式如下:
(7)
将式(7)代入式(6),并且令:
(8)
对式(8)等式两边对时间t进行微分处理,可将表达式转换为:
dz=σzdt
(9)
根据上述变化,代入到式(6),可得到可靠度指标的具体表达式
(10)
3 扶壁式码头受力分析及结构稳定计算式分析
重力式扶壁码头主要通过肋板与立板来产生挡土左右,保证码头各部分连成整体。扶壁码头肋板施工主要在现场浇筑。该类型码头施工工艺简单、施工速度快。
根据重力式扶壁码头的受力分析,可得到其抗滑稳定性功能函数以及扶壁码头的抗倾覆稳定性功能函数分别见式(11)和式(12)。
Zs=fG-(EhKp1+PW+Eqh+ERH)
(11)
Zu=Kp2Mfb-(Kp1Mh+Mpw+Mq+MPR)
(12)
式中,f为摩擦系数;G为码头总自重;Eh为竖向土压力;Kp1为主动土压力系数;Pw为剩余水压力;Eqh为作用在码头面荷载的竖向分力;ERH为系缆力的竖向分力。
4 实例工程概况
4.1 工程地理位置
本工程位于泰州城北物流园区西南部,泰州市新通扬运河北岸,新通扬运河与引江河的丁字交叉口西侧约1.1 km处,《泰州市城北物流园区控制性详细规划》中7B号内河港池地块。
4.2 地形地貌
泰州市海陵区内以通扬公路为界,北部属里下河平原区,南部属长江三角洲平原区。均为地质年代的第四系沉积物所覆盖。地面以下400~1 400 m的基岩是玄武岩的“古潜山”。本区为扬子准地台的一部分,地质属新生代。境内构筑地基的结构层,由于成因类型各异,构成地基土也截然不同,因其上部地基土承载力标准值不同,大体上可分为良好区、软土区、杂填区和不良区4个工程地质区。全区地势平坦,南高北低,南部多属平地,北部河网密布,地面标高2.6~5.5 m,最高处岳阜标高20.28 m。
4.3
实例工程处的地质性质,自上而下分为5个层次。场地内土层分布较均匀。各土层自上而下描述如下:
(1)层耕土:灰褐色,松散,稍湿,主要由粉质粘土组成,上部含植物根等。场区普遍分布,厚度:0.80~1.80 m,平均0.90 m;层底标高:0.65~2.11 m,平均1.74 m;层底埋深:0.80~1.80 m,平均0.90 m。
(2)-1层粉质黏土:灰褐色,湿,软塑~可塑,稍有光泽,中等干强度,中等韧性。场区普遍分布,厚度:1.7~3.20 m,平均2.70 m;层底标高:-2.25~2.11 m,平均-0.73 m;层底埋深:0.80~4.00 m,平均3.44 m。
(3)-2层粉质黏土夹黏土:黄褐色,湿,可塑~硬塑,光泽,高干强度,高韧性,含铁锰结核。场区普遍分布,厚度:5.10~8.20 m,平均6.03 m;层底标高:-9.36~-6.08 m,平均-6.98 m;层底埋深:7.80~12.20 m,平均9.67 m。
(4)层粉土:灰黄~灰色,含钙质结核,很湿,稍密~中密,摇振反应中等,无光泽反应,低干强度,低韧性,场地东北角局部分布,厚度:2.80~2.90 m,平均2.85 m;层底标高:-12.16~-9.70 m,平均-10.93 m;层底埋深:12.60~15.00 m,平均13.80 m。
(5)-1层粉质黏土:灰黄色,可塑,稍有光泽,中等干强度,中等韧性。场区普遍分布,厚度:4.50~10.80 m,平均9.43 m;层底标高:-17.85~-16.48 m,平均-16.78 m;层底埋深:18.20~20.20 m,平均19.49 m。
(6)-2层粉质黏土夹黏土:黄褐色,可塑-硬塑,含铁锰结核,稍有光滑面,切面规则,夹少量钙质结石。场区普遍分布,厚度:5.70~6.70 m,平均5.94 m;层底标高:-23.75~-22.30 m,平均-22.72 m;层底埋深:24.10~26.30 m,平均25.43 m。
(7)层粉土夹粉砂:灰黄~灰色,含钙质结核,饱和,稍密~中密,摇振反应中等,无光泽反应,低干强度,低韧性,所夹粉砂灰色,组成矿物成份主要为石英、长石等,具云母碎屑,颗粒级配良好(SW),次园状,粘粒含量低。场区普遍分布,该层未穿透。
4.4 总平面布置
在港池东西两侧驳岸各布置2个泊位,装卸机械均采用固定吊起重机。港池东西驳岸长度均为160 m,港池宽度为60 m,占用自然岸线总长度为240 m,占用实际岸线长度为380 m,港池底高程取为-3.0 m。港池与新通扬运河间布置连接水域,以保证船舶安全便捷的进出港作业,连接水域直线部分长13 m,弧线部分为1/4半径60 m的圆弧,连接水域宽60 m,底标高取为-3.0 m。连接水域护岸采用坡比为1∶2的斜坡式结构,连接水域外侧新通扬运河上下游护岸各长30 m。
4.5 码头结构方案
码头采用钢筋混凝土扶壁式结构。码头顶标高4.40 m,港池底标高-3.00 m,扶壁式底板宽9 m,厚0.7 m下设100 mm素混凝土垫层;前处趾设0.7 m厚的浆砌块石护趾;立板厚0.5 m,肋板厚0.5 m,标准段肋板间距4.5 m。顶部胸墙墙高1.3 m,宽1.2 m;护轮坎高0.3 m。码头水工建筑物结构标准分段长13 m,端部分段长15 m,拐角处3.18 m、过渡段10 m),沉降缝宽2 cm,采用聚乙烯板(PEB3)填充,墙后缝宽处自上而下贴全宽150 cm的400 g/m2无纺土工布。港池端部结构采用同样的钢筋混凝土扶壁式结构。顶标高为4.40 m,底标高-3.00m。
5 实例码头工程结构稳定性计算及优化分析
将实例码头工程的详细参数代入式(11)与式(12),再分别代入式(10),可分别得到码头结构抗滑安全和抗倾覆安全的可靠度指标。由于式(10)及相关计算步骤繁琐,计算难度较大,因此本文通过Matalab进行编程计算。
根据上式计算结果,实例码头安全系数远远满足稳定要求(详细计算结果见表1),为节约投资,提高工程经济性,将码头整体断面按1%比例的步长逐渐缩小,即以原码头工程断面结构为基本参照,依次按照99%、98%、97%...的比例计算,直到求得抗力与作用效应刚好满足《重力式码头设计与施工规范》(JTS 167-2-2018)的要求时的断面结构,将这两种情况下的抗滑稳定性和抗倾覆稳定性可靠度指标的计算结果列于下表。
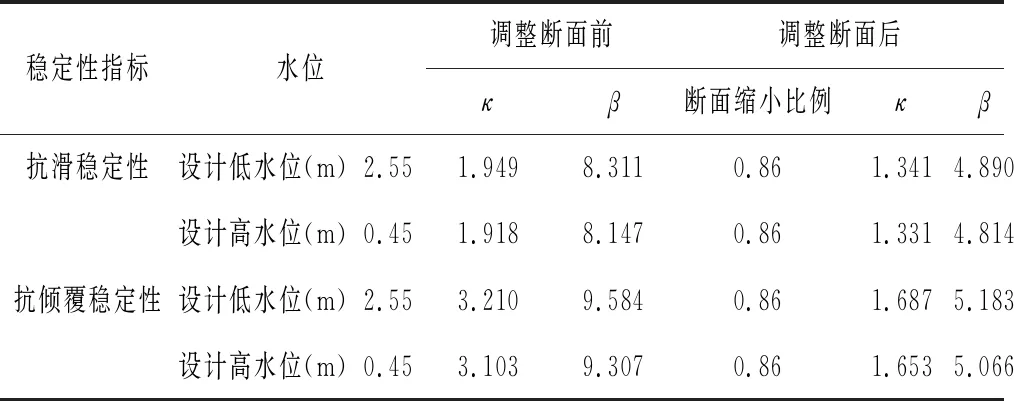
表1 实例工程优化前后可靠度指标计算结果
6 扶壁码头结构稳定系数与可靠度指标的相关关系研究
笔者搜集了另外35个扶壁码头实例工程的相关数据,以设计高水位为计算工况,根据前两节相应的计算流程、公式,借助MATLAB编程进行计算,将计算结果汇总于图1和图2。
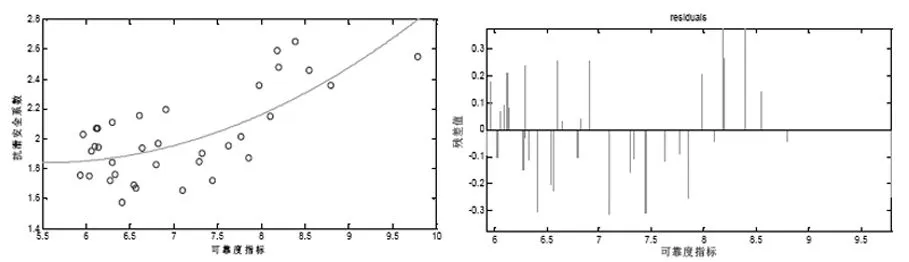
图1 扶壁码头抗滑安全系数Ks与可靠度指标β的相关关系
(1)抗滑安全系数与可靠度指标的相关关系
根据图1可看出,扶壁码头的抗滑安全系数Ks与可靠度指标β呈显著的正相关关系,且二者的函数关系趋近于乘幂曲线。因此,可得到二者关系结构式:
Ks=αβb+c
(13)
式中,a、b、c均为待定系数,在已有资料基础上经过多元回归分析,得到扶壁码头的抗滑安全系数Ks与可靠度指标β的关系表达式:
Ks=0.526 9β0.683 9+0.001 7
(14)
式(14)中扶壁码头的抗滑安全系数Ks与可靠度指标β相关系数较低,仅有0.428 1。
(2)抗倾覆安全系数与可靠度指标的相关关系
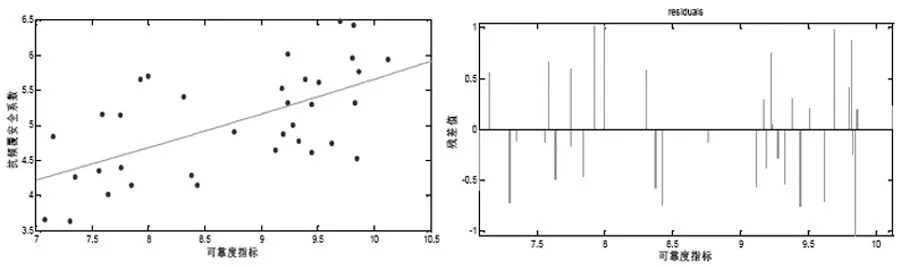
图2 扶壁码头抗倾覆安全系数Ku与可靠度指标β的相关关系
根据图2可看出,扶壁码头的抗倾覆安全系数Ku与可靠度指标β呈显著的正相关关系,且二者的函数关系趋近于乘幂曲线。根据计算结果进行多元回归分析,得到扶壁码头的抗倾覆安全系数Ku与可靠度指标β的关系表达式:
Ks=0.816β0.837 7-0.012 5
(15)
进一步分析可知,式(15)中扶壁码头的抗倾覆安全系数Ku与可靠度指标β相关系数较低,仅有0.392 1。
7 结 论
(1)详细介绍了可靠度指标的定义和计算式。并通过受力分析,得到了重力式扶壁码头抗滑稳定性可靠度和抗倾覆稳定性可靠度的表达式。
(2)以泰州内河港7B码头工程为实例详细计算了其结构稳定性。计算结果显示,实例工程的抗滑稳定系数和抗倾覆稳定系数分别为1.918~1.949和3.103~3.210,均远大于规范要求,结构设计安全。
(3)将码头整体断面按1%比例的步长逐渐缩小,在满足规范结构安全的前提下,对实例工程码头结构进行优化,研究结果显示,断面可缩小至86%。
(4)采用回归分析,拟合了扶壁码头结构稳定系数与可靠度指标的相关关系。研究结果显示,扶壁码头的抗滑安全系数和抗倾覆安全系数均与可靠度指标呈乘幂指数关系,但相关性较差。
