抽水蓄能电站参与电力现货市场竞价多日滚动优化运行方法

2021-01-14刘小敏李海明

水力发电 2020年10期

余涛，刘小敏，俱鑫，李海明

(国网宁夏电力有限公司，宁夏银川 750000)

电力现货市场是电力市场体系的重要环节，对电力市场的开放、竞争、有序运行起到了支撑作用[1-2]。2019年《关于深化电力现货市场建设试点工作的意见》中指出，现货市场对各主体的重要性，即用电客户主体可发现价格信息、电网主体为电力短期供需平衡提供市场化手段、新能源主体兼顾新能源等特点，有利于扩大新能源消纳空间[3]。基于此，研究以现货市场为主的各类主体竞价策略具有重要意义。

在电力现货市场中，对不同的市场主体研究竞价与运行策略是一门重要课题。抽水蓄能电站作为一种特殊的电源形式和电力现货市场参与主体，在现代电网中的应用越来越广泛[2]。目前已有较多文献针对抽水蓄能电站优化运行方法提出模型，文献[4]提出了采用抽水蓄能电站配合光伏发电运行提高系统的可靠性并建立其优化运行模型；文献[5]根据混合式抽水蓄能电站的功能和特点，构建了包含混合式抽水蓄能电站的库群联合优化调度通用模型；文献[6]建立了含风电场和抽水蓄能电站的电力系统动态优化调度模型。然而以上文献并没有考虑抽水蓄能电站参与电力现货市场运行计划的影响。

另外也有一些文献研究了抽水蓄能电站参与电力市场的行为，文献[7]考察了抽水蓄能电站参与电力市场的价格机制，但针对的是辅助服务市场而不是电力现货市场。文献[8]结合抽水蓄能电站水库水头与储能之间的关联关系，确定了机组最优的发电出力投标，但建立的模型未考虑电力现货价格的不确定性。目前还很少有文献针对抽水蓄能电站参与电力现货市场，计及系统运行特性建立其竞价和运行模型。

事实上，许多文献制定抽水蓄能电站运行计划的时间范围都为一天，并且设定一天始末时段剩余水量相同。而在多日范围内运行时，在抽水蓄能电站竞价与运行模型中，电站初始水头对目标函数的影响较大。若初始水平较高，并且一天内前期时段电力现货价格较低，那么电站能够竞标购电的电量有限，降低了经济效益；若初始水头较低，且一天内前期时段电力现货价格较高，那么电站能够竞标售电的电量有限，同样降低了经济效益。而这样的效益需要在长期的竞价和运行中才能体现出来，因此本文采用多日滚动运行方式进行优化，同时对抽水蓄能电站的初始水量也进行优化。

本文采用多日滚动优化方法，依据电力现货价格预测曲线，计及不确定性制定下一个交易日内抽水蓄能电站参与电力现货市场的竞价和运行策略。对量子粒子群算法引入自适应概率选择进行改进，并采用改进量子粒子群算法求解所建立的模型。最后通过算例验证了本文方法的有效性。

1 抽水蓄能电站竞价运行策略

1.1 目标函数

抽水蓄能电站在电力现货日前市场各时段既作为发电商参与竞价，也作为负荷参与竞价。在t时段抽水蓄能电站运行在发电商模式，向电力调度交易中心申报竞标出力电价Qb(t)和竞标出力电量Pb(t)作为模型的控制变量；在t时段抽水蓄能电站运行在负荷模式，向电力调度交易中心申报竞标购电电价Qp(t)和竞标购电电量Pp(t)，得到抽水蓄能电站一天之内参与电力现货市场获得收益作为优化模型的目标函数，收益表达式为

(1)

式中，T为一天内电力现货市场时段数；c1(t)为抽水蓄能电站售电竞价系数，当c1(t)=1时表示电站在t时段运行在发电商模型；c2(t)为抽水蓄能电站购电竞价系数，当c2(t)=1时表示电站在t时段运行在负荷模式；d1(t)为电站在t时段的发电中标系数，d1(t)=1时为中标，d1(t)=0时为未中标；d2(t)为电站在t时段的购电中标系数，d2(t)=1时为中标，d2(t)=0时为未中标；QMCP(t)为t时段电力现货市场预测出清价格，本文采用统一市场出清价格机制(market clearing price，MCP)进行市场出清[9]。

式(1)中c1(t)和c2(t)同样作为抽水蓄能电站的控制变量，作为制定各时段运行模式的依据。d1(t)和d2(t)实际上为随机变量，由电站竞价情况和电力现货预测出清价格的关系决定，其表达式为

(2)

(3)

1.2 约束条件

抽水蓄能电站在既定的中标情况下制定系统的一天运行计划，满足如下约束：

(1)运行模式约束。抽水蓄能电站在任意时段只能运行一种模式，因此有竞价系数约束。该约束表示为

(4)

(2)抽水蓄能电站出力约束。由于抽水蓄能电站运行工况的限值，电站无论是在发电状态还是负荷状态，运行功率均存在限值。该约束表示为

(5)

(3)一天水量平衡约束。为了保持抽水蓄能电站持续的抽水-发电状态，电站的剩余水量在一天首末时段需要满足的约束为

(6)

式中，WT为末时段水量；W0为初始时段水量；r为抽水蓄能电站的功率-水量转化系数；η为抽水蓄能电站的循环系数，一般取为0.75。

(4)电站库容约束。抽水蓄能电站在一天各时段需要满足电站的库容不超过最高水头和允许的最低水头。该约束为

(7)

式中，W0为电站初始时段水头；Wmin和Wmax为最小库容和最大库容。式中该约束需要对k=1，2，…，T均成立。

2 基于不确定二层规划的多日滚动优化

由于MCP价格在以一周为周期内存在一定的规律性[10]，同时过长的滚动时间窗口难以满足电力现货价格预测的精度，而过短的滚动时间窗口发掘抽水蓄能电站经济性的效果又有限，因此综上考虑本文制定的抽水蓄能电站多日滚动时间窗口选取为一周。假设系统在运行日k前一天制定竞价和运行计划，采用期望值二层规划模型建模，具体表达式为

(8)

x由下式决定：

(9)

式中，fk()为运行日k的目标函数，具体如式(1)所示；E[]为期望值函数；下层模型的控制变量为x=[c1，c2，Qb，Qp，Pb，PP]，其中c1和c2分别为售电竞价系数向量和购电竞价系数向量，Qb和Qp为售电竞价向量和购电竞价向量，Pb和PP为售电竞标电量向量和购电竞标电量向量；随机变量为ξ=[QMCP]，其中QMCP市场出清电价向量。上层模型的控制变量为W=[Wk+1，…，Wk+7]，但上层模型不能直接决定自身的目标函数，通过影响下层模型的决定来间接影响；而下层模型在上层模型的决策基础上才能进行优化，将优化结果向上层模型反馈。

3 量子粒子群算法

3.1 改进量子粒子群算法

本文对量子粒子群算法(quantum particle swarm optimization，QPSO)引入自适应概率选择进行改进[11]。QPSO算法中，量子位和相角用来描述粒子的状态，而不是用传统PSO算法中粒子的位置和速度。量子位是QPSO算法中用数对定义的最小单元，表示为

(10)

式中，αji和βji分别表示量子位所处的状态“0”和“1”的概率，满足

(11)

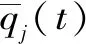
(12)

qji(t)=[αji(t);βji(t)]

(13)

量子位能够代表具有概率行为的所有可行解的线性叠加。2n+1种个体可由量子位的不同状态组成。用量子位表示比用其他形式的表示在产生种群多样性方面更有优势。因为归一化条件，量子相位表示为

(14)

式中，0和1表示量子位处于0和1状态的概率，QPSO的更新机制是通过进化量子位和量子相角，且量子位满足了归一化条件。其中，量子旋转门的更新公式表示为

(15)

为了得到αji和βji的迭代关系，将式(14)代入式(15)，得到表达式为

(16)

式中，αji(t+1)和βji(t+1)分别表示在时刻，量子位所处的概率。

在种群多样性方面，量子旋转门和量子位具有一定优势，但收敛效果一般，本文通过引入自适应概率选择进行改进。具体做法：定义个体亲和力值，以升序方式计算每个个体在当前种群和重组后种群中的适应值，并采用个体量子位位置指数表示亲和力值，表达式为

(17)

式中，As[]表示取亲和力值；r为(0，1)上的随机数。上述定义的特别之在于：亲和力值仅与位置指数相关，与实际适应值无关，避免了早熟收敛问题。然而，个体集中度函数Cs[]的定义，即式(18)，其中Ks[]为量子位范式距离判别函数，可定义为如下形式。

(18)

(19)

在计算选择概率时，主要采用轮盘选择法，给每个量子位个体分配一个被选中的概率，用Ps[]表示某事件的概率测度函数，则该概率为

(20)

因此，根据被选中个体选择概率，保证了量子位个体中具有较高亲和力值的个体被选中，其他个体将被排除，使得QPSO一直在全局最优值处进行收敛。

3.2 多日滚动模型求解流程

假设当前运行日为k，制定运行日k+1的竞价和运行策略，滚动时间范围为7日，滚动时间窗口为一天。根据改进量子粒子群算法原理得到本文制定的抽水蓄能电站多日滚动竞价与运行策略的上层模型步骤如下：

(1)预测k+1日之后7日内的MCP价格曲线，首先调用上层模型优化k+1日剩余水量Wk+1。

(2)初始化量子粒子群算法参数，以Wk+1为粒子的量子位和相角，初始化粒子种群。

(3)对每一个粒子，将Wk+1输入到下层模型中，得到下层模型提供的反馈即抽水蓄能电站一天期望收益。

(4)计算每个粒子的适应度函数，并采用量子旋转门更新公式对每个粒子的量子位和相角进行更新。

(5)采用自适应概率选择对粒子种群进行进一步寻优。

(6)判断算法收敛性，如果收敛，则输出当前迭代结果，否则返回步骤(3)。

抽水蓄能电站多日滚动竞价与运行策略的下层模型步骤如下：

(1)预测k+1日之后7日内的MCP价格曲线，输入上层模型提供的k+1日剩余水量Wk+1。

(2)初始化量子粒子群算法参数，以x为粒子的量子位和相角，初始化粒子种群。

(3)对应每一个粒子，采用蒙特卡洛随机模拟技术得到下层模型抽水蓄能电站一天期望收益。

(4)计算每个粒子的适应度函数，采用量子旋转门更新公式对每个粒子的量子位和相角更新。

(5)采用自适应概率选择对粒子种群进行进一步寻优。

(6)判断算法收敛性，如果收敛，则输出当前迭代的抽水蓄能电站一天期望收益并反馈给上层模型，否则返回步骤(3)。

4 算例与分析

4.1 算例设置

本文以某典型抽水蓄能电站参与电力现货市场为例进行仿真分析，制定该电站的竞价策略和运行计划。为了便于计算，该电站的库容等效转化为可发电功率，最低库容为500 MW·h，最高库容为2 000 MW·h，假设当前运行日的抽水蓄能电站初始剩余电量折算为电量为1 000 MW·h，采用本文的滚动优化方法，制定对次日电力现货市场的竞价方案以及系统的运行计划。电力现货市场一天分为48个时段，每个时段0.5 h，抽水蓄能电站需要针对各时段申报竞价和出力电量。根据文献[12]，电力现货市场价格采用一阶自回归模型来描述，而该模型中回归误差满足正态分布，对电力现货市场电价采用正态分布进行模拟。量子粒子群算法中，本文设定抽水蓄能电站的2种运行方式：方式一为参考大部分文献对抽水蓄能电站每个交易日首末时段的剩余水量保持一致；方式二为采用本文的模型对每个交易日末的剩余水量进行优化。

假设当前运行日对未来7日内MCP价格曲线的预测如图1所示。

图1 滚动优化时间窗口内MCP电价预测曲线

从图1看出，MCP价格曲线基本上以天为单位存在周期性，同时在不同交易日内又存在不同。

4.2 仿真结果与分析

运行提出的模型，得到抽水蓄能电站代理对制定的参与次日日前市场的各时段竞价曲线以及各时段竞标出力曲线如图2所示，同时在该竞价策略下的系统运行策略如图3所示，运行策略包括制定的抽水蓄能电站充放电计划以及剩余水量曲线。图2中当竞标电价大于零时表示参与发电市场竞价，当竞标电价小于零时表示参与购电市场竞价。图2中当竞标电量大于零时表示参与发电市场竞价，当竞

图2 抽水蓄能电站参与电力现货市场竞价策略

图3 抽水蓄能电站充放电功率曲线和剩余水量曲线

标电量小于零时表示参与购电市场竞价。当竞标电价和竞标电量均等于零时表示抽水电站既没有参与发电侧市场也没有参与购电侧市场。

从图2和图3看出，抽水蓄能电站代理制定的竞价策略和竞标电量策略充分计及了MCP电价曲线的趋势。在一天的第1时段到第四时段，尽管MCP电价水平较低，但抽水蓄能电站初始剩余水量水平较高，仍可通过售电获得一定的收益，而降低的水量可以通过后续的第5时段到第8时段更低的MCP价格进行补充。在第9时段到第19时段，抽水蓄能电站基本上既没有参与发电侧市场也没有参与购电侧市场。在第20时段到第24时段，抽水蓄能电站参与发电侧市场，并申报较高的电价和出力以便通过较高水平的MCP电价获取收益，同时为了增加中标的把握，抽水蓄能电站申报的电价均要略高于MCP价格。在第25时段到第37时段，由于MCP价格高峰已过，抽水蓄能电站即存在参与发电侧市场的时段也存在参与购电侧市场的时段，同时报价策略较为激进，主要因为在这些时段不中标导致的收益降低风险较小。在第38时段到第43时段，MCP价格迎来了第二次高峰，抽水蓄能电站又一次在发电侧市场申报尽可能高的出力以及较为保守的竞价；在一天最后的第44时段到第48时段，抽水蓄能电站通过较为低廉的MCP电价对剩余水量进行补充，以便达到上层模型制定的水平。

事实上，通过以上竞价策略以及运行策略，抽水蓄能电站能够获得的一天期望运行收益为60 960.6元，多日滚动优化模型中，上层模型制定的次日末时段抽水蓄能电站剩余水量水平为1 636.5 MW·h。计算一天各时段的抽水蓄能电站运行成本收益可以得到如图4所示的曲线。

图4 抽水蓄能电站各时段运行成本收益曲线

从图4中看出，当抽水蓄能电站参与发电侧市场时，系统获得收益，当参与购电侧市场时，系统需要支付成本。抽水蓄能电站的主要收益来源于MCP电价曲线的两次高峰时段。

事实上，根据预测的短期MCP价格曲线，可以得到当前滚动时间窗口内抽水蓄能电站制定的竞价策略和运行计划下的各个交易日内的系统运行指标如表1所示。

表1 抽水蓄能电站参与电力现货市场期望运行指标

从表1中看出，上层模型制定的各运行日末时段抽水蓄能电站剩余水平与MCP价格水平密切相关。在第2交易日，第4交易日，第6交易日以及第7交易日内，MCP价格水平较高，因此上层模型制定的当前运行日末，第3交易日末，第5交易日末以及第6交易日末的电站剩余水量水平较高；而第3交易日，第5交易日的MCP价格水平较低，因此制定的第2交易日以及第4交易日末的电站剩余水量水平较低。

对电力现货市场电价采用正态分布进行模拟，并采用本文的滚动优化模型使得系统实际运行到第7交易日，可以得到抽水蓄能电站参与电力现货市场期实际运行指标如表2所示。

从表2看出，由于MCP价格的预测存在误差，多日滚动优化模型中制定的抽水蓄能电站运行计划可能不适用于实际，因为实际的MCP价格曲线影响到了电站的中标情况，也导致了实际的运行收益与期望收益存在偏差。通过多日滚动运行采用较优的方式实时更新当前运行日的末时段剩余水量以及竞价策略，获得更高的收益。

表2 抽水蓄能电站参与电力现货市场期实际运行指标

为了比较方式一和方式二下的电站运行指标情况，在对MCP电价曲线模拟十次的情况下分别在2种方式下采用同样的方式运行本文所建立的模型，可以得到2种方式下的运行指标对比如表3。

表3 两种运行方式下运行指标对比

从表3中看出，无论滚动周期内期望收益平均还是滚动周期内实际收益平均，方式二下的指标均优于方式一下的，这说明通过多日滚动优化方式对各交易日末时段剩余水量进行优化能够显著提升抽水蓄能电站的运行收益。同时由于方式二相比于方式一更加灵活可调，因此抽水蓄能电站收益对MCP电价的不确定性更加具备鲁棒性，所以方式二下的滚动周期内期望收益标准差和滚动周期内实际收益标准差指标均优于方式一。

为了比较本文改进量子粒子群算法的求解效果，以方式二为例，对建立的模型采用基本粒子群算法、量子粒子群算法以及本文改进量子粒子群算法进行10次求解，得到3种情况下的模型求解指标对比如表4所示。