考虑基土不均匀冻胀的梯形渠道混凝土衬砌弹性地基梁力学模型

李宗利，姚希望，张 锐，邵化建，王正中

考虑基土不均匀冻胀的梯形渠道混凝土衬砌弹性地基梁力学模型

李宗利1,2，姚希望1，张 锐1，邵化建1，王正中1,2

（1. 西北农林科技大学水利与建筑工程学院，杨凌 712100；2. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

为了探究寒区高地下水位引起基土和衬砌板耦合非均匀变形对梯形渠道衬砌内力变化影响规律，该研究在前期提出的弹性地基梁模型基础上，将衬砌板与基土相互作用效应分解为基土不均匀自由冻胀位移、衬砌板受到冻土反作用产生的位移和边坡衬砌板坡脚约束产生的相对转动位移，从而建立了满足两端变形协调的弹性地基梁模型。以甘肃省高液限土壤，地下水位5 m地区的边坡系数为1 的渠道为例，探究不同边坡衬砌板长度和不均匀冻胀基土之间的相互作用。结果表明，边坡衬砌板长度每增加1 m，冻胀反力最大值增大142%，弯矩最大值平均增大223%，弯矩最大值点会从原来的距坡脚1/3 左右处向坡脚偏移。以边坡衬砌板长度为4 m为例，探究了基土均匀冻胀和不均匀冻胀对边坡衬砌板影响的差异，得出基土不均匀冻胀的冻胀反力最大值和弯矩最大值，分别比基土均匀冻胀大264%和170%。因此，在寒区高水位地区进行渠道抗冻胀衬砌设计时，宜按基土非均匀冻胀弹性地基梁模型计算。

渠道; 模型；混凝土；不均匀冻胀；冻胀；弹性地基梁；冻土工程

0 引 言

研究表明[1-5]，地下水对基土冻胀有着显著的影响。当土壤达到冻结温度以下，土壤中水开始发生结冰膨胀，未冻区的水分会向冻结区迁移，加之地下水的补给作用，冻结区的冻胀作用会进一步加剧，距离地下水位越近，其冻胀效果越显著。因此，在寒区高水位地区的梯形渠道，由于边坡衬砌板各计算点和地下水位之间的距离存在差异，导致其基土的自然冻胀量沿边坡衬砌板方向呈现差异化的分布。

弹性地基梁理论能够较好地反映基础和上层结构的相互作用[6-7]。基于该理论，肖旻等[8]认为冻胀量和冻胀力成正比，推导出考虑冻土与衬砌板相互作用的渠道衬砌板冻胀后的挠曲线方程，给出内力的解析表达式，为渠道冻胀设计提供参考；李宗利等[9]改进了以往将渠道冻胀分析[10-16]中将衬砌板两端边界条件，通过分析渠道衬砌板冻胀过程中的受力和变形特点，基于渠道基土自然冻胀量，重新建立渠道冻胀破坏的弹性地基梁力学模型，得到的冻胀量和冻胀力分布与实际更为相符。然而以往这些渠道冻胀力学模型并未考虑渠道衬砌板对基土发生不均匀冻胀的响应问题。

基础的不均匀变形是影响上层工程结构发挥正常作用的一个重要制约因素。郑永来等[17]基于某地地铁隧道的纵向沉降数据，分析纵向沉降对隧道结构安全性的影响，建立隧道纵向变形曲率与隧道管片接头环缝张开量之间的关系，为工程设计提供依据。狄宏规等[18]基于南京地铁1号线运行后约4 a的观察数据，分析其沉降发展的时空变化特征，得出其不均匀沉降的主要原因，并提出对于软土地区地铁隧道的不均匀沉降问题，应结合工程地基条件和周边建筑的开发程度，进行分区预控制。冻土地区的不均匀冻胀也是地基不均匀变形的一种形式。黄继辉等[19]推导出考虑围岩不均匀冻胀性的寒区圆形冻胀力解析解。围岩不均匀冻胀性是引起寒区隧道围岩中冻胀力的重要原因，在合理的围岩弹性模量和不均匀冻胀系数取值范围内，解析解的计算结果和实际情况吻合较好。目前基础不均匀变形对上层工程结构的研究在隧道和管线中研究相对较多[17-20]，但在渠道中却研究相对较少。

本研究在前期[9]提出的弹性地基梁模型基础上，将渠道衬砌板与基土相互作用效应分解为基土不均匀自由冻胀位移、衬砌板受到冻土反作用产生的位移和边坡衬砌板坡脚约束产生的相对转动位移，从而建立了满足两端变形协调的弹性地基梁模型。分析不同边坡衬砌板长度和不均匀冻胀基土之间的相互作用和基土均匀冻胀和不均匀冻胀对边坡衬砌板影响的差异，以期为寒区高水位地区的渠道混凝土衬砌的抗冻胀设计提供参考。

1 渠道基土冻胀量与地下水位的关系

1.1 冻胀率沿渠道断面分布规律

如图1所示，计算点至地下水位的距离根据几何关系可得

式中H()为计算点至地下水位的距离，m；H为渠顶距地下水位的距离，m；为边坡系数；为计算点到渠顶的距离，m。

注：、两点为边坡衬砌板顶点；、两点为渠道坡脚点；H为渠顶距地下水位的距离，m；H为渠底距地下水位的距离，m；H()为计算点至地下水位的距离，m；为边坡系数；为计算点到渠顶的距离，m；L为边坡坡脚点，m；L为、点间长度，m。

Note: The two pointsandare the apex of the slope lining plate; The two pointsandare the slope foot points of the canal;His the distance from the top of the canal to the groundwater level, m;His the distance from the bottom of the canal to the groundwater level, m;H() is the distance from the calculation point to the groundwater level, m;is the slope coefficient;is the distance from the calculation point to the top of the canal, m;Lis slope foot point, m;Lis distance fromto, m.

图1 地下水与渠道衬砌板的几何关系图

Fig.1 Geometric relationship between groundwater and canal lining slabs

研究表明[1-4]，冻胀率与地下水位之间的关系可表示成负指数形式

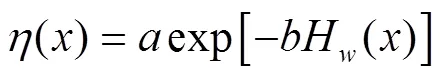
式中()为冻胀率，%；、为与特定地区、特定气象、水分、土质条件有关的经验系数，常根据试验数据由最小二乘法拟合获得。

1.2 冻胀量沿渠道断面分布规律

垂直自然冻胀量会沿边坡衬砌板的切向和法向方向产生2个分量，则边坡基土的竖直自然冻胀量y()（m），法向自然冻胀量y()（m）和切向自然冻胀量y()（m）分别为

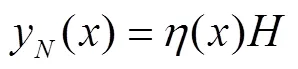
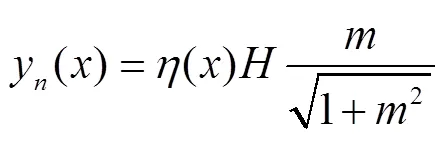
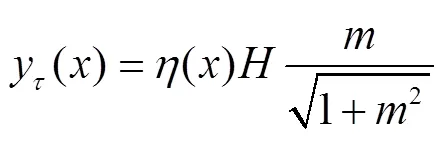
式中为基土冻深，m。

2 考虑基土不均匀冻胀的梯形渠道混凝土衬砌冻胀弹性地基梁力学模型的建立

在文献[9]建立的梯形渠道混凝土衬砌冻胀弹性地基梁力学模型的基础上，本文考虑基土不均匀冻胀对渠道混凝土衬砌冻胀的影响。

2.1 基本假设及简化

本文在文献[9]中基本假设及简化的基础上再提出以下2点：

1）影响土体冻胀的因素很多，但是归纳起来不外乎土的粒度组成、矿物成分、土中水分、孔隙率、温度、荷载以及盐分等[21]。而土体冻胀的主要原因为冻结过程中的水分迁移和析冰作用[22]。在寒区高水位地区地下水对土体的冻胀起到主导作用，因此本文仅考虑由地下水引起的基土不均匀冻胀，暂忽略其他次要因素对不均匀冻胀的影响；

2）渠底衬砌板一般为水平铺设，若不考虑阴坡和阳坡温度的不同，可认为渠底衬砌板和地下水位始终为平行关系，渠底基土只发生均匀冻胀。因此，渠底衬砌板可根据文献[9]进行计算，本文不再重复。

2.2 边坡衬砌板冻胀弹性地基梁力学模型

根据文献[9]得出边坡衬砌板挠度y()、弯矩M()和剪力V()计算式分别为

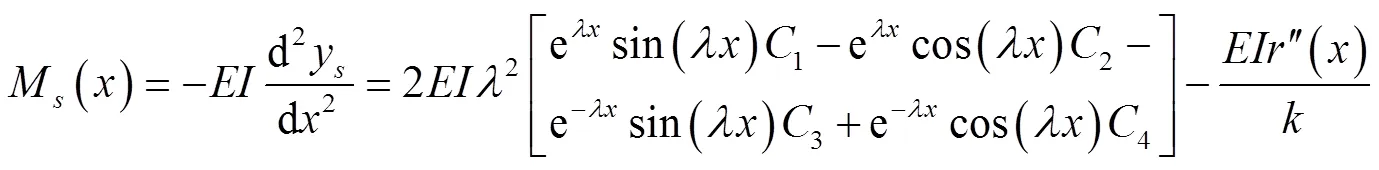
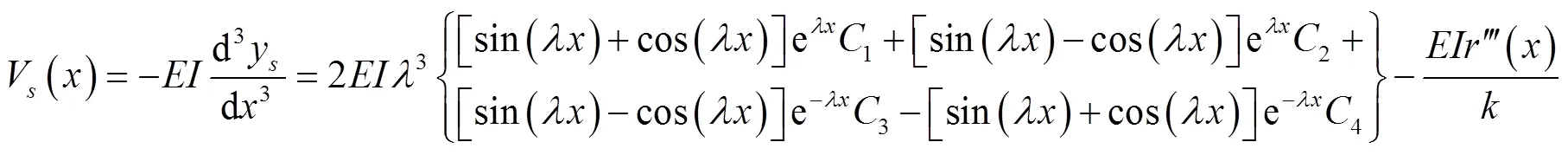
令

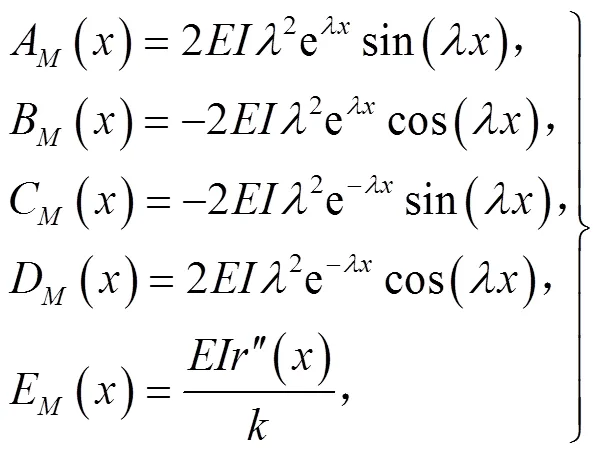
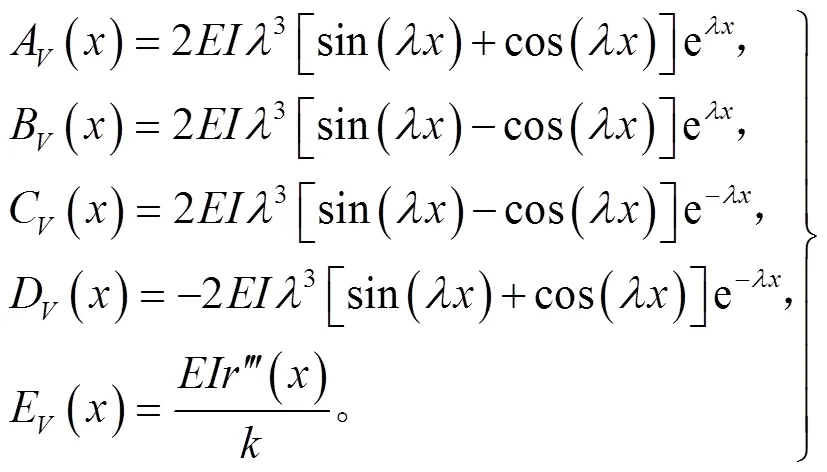
将式（9）和式（10）分别代入式（7）和式（8）中，则有

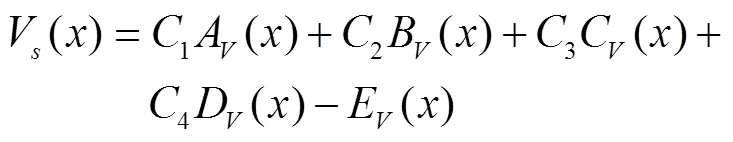
根据式（4）和图2b可知，在高水位地区，渠道基土在自然冻胀的情况下，冻胀量沿边坡衬砌板方向不均匀的分布。图2c所示，先不考虑坡脚约束，在边坡基土冻胀过程中，边坡衬砌板和渠道基土紧紧地冻结在一起，加之边坡衬砌板的存在一定的刚度，因此边坡衬砌板会对基土不均匀冻胀的有一定的约束作用，同时产生一定的附加应力（r()）。如图2d所示，在边坡衬砌板发生冻胀时，渠道衬砌板在基土冻胀的作用下发生一定的冻胀位移。坡脚附近由于渠道底板的存在，对其冻胀有一定的约束作用（F和F）。因此，在高水位地区的渠道边坡衬砌板不仅受到来自底板的约束作用，而且也受到来自不均匀冻胀产生的附加应力。为了简化数学上的计算，将图2d转化为图3中的相对冻胀线进行分析计算。

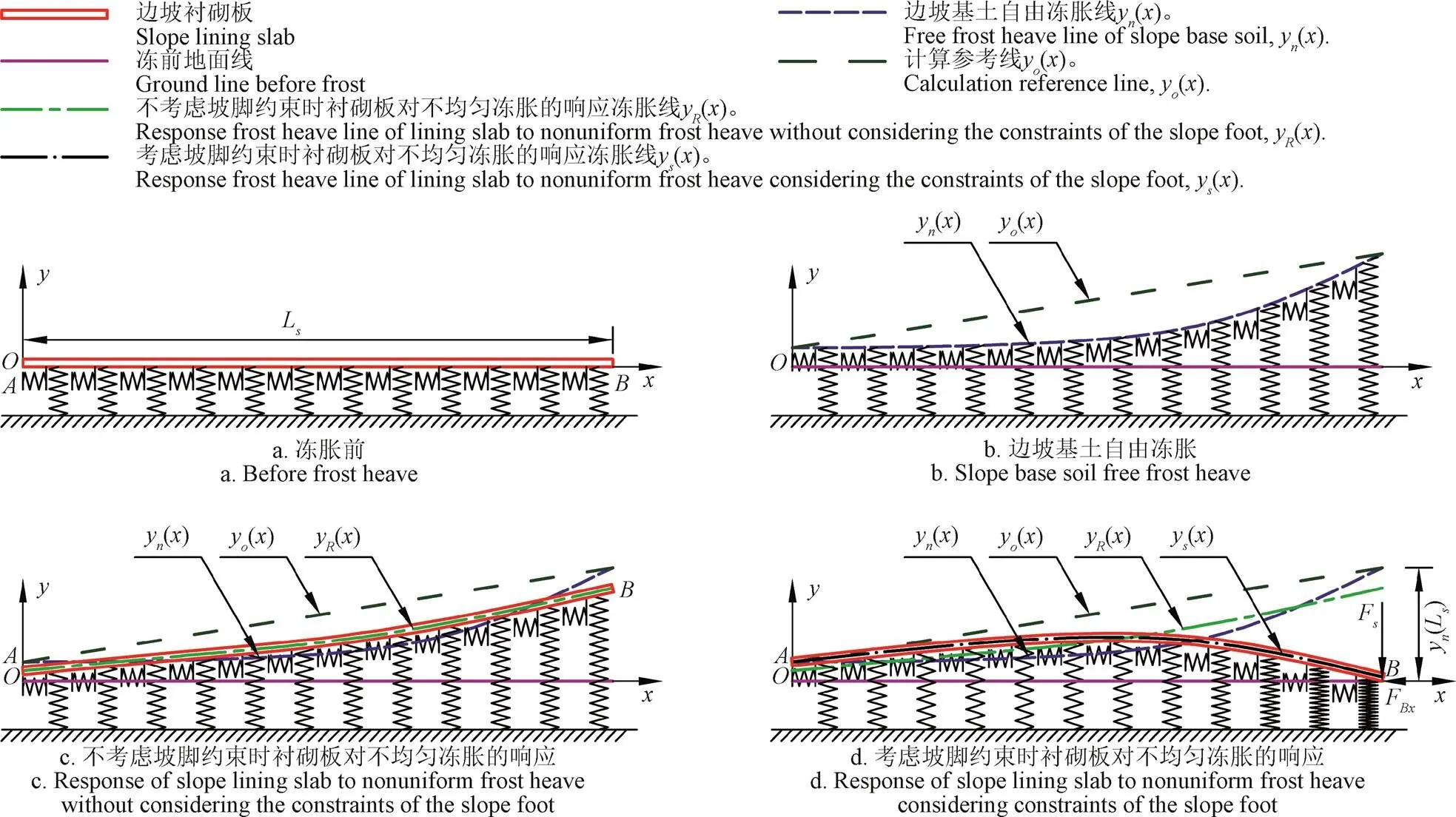
注：yn为法向自然冻胀量，m；Fs和FBx为渠底衬砌板对边坡衬砌板在坡脚处的约束反力，N。

在很多基础的不均匀变形和基础上结构相互影响分析中，往往不容易直接计算出基础上结构自身变形的情况，但可以间接地由基础变形来分析基础上结构的变形。一般可通过等价荷载法，位移叠加法或近似解法来求基础上结构的变形[23]。本文采用等价荷载法对在边坡衬砌板在基土不均匀冻胀的情况下的力学响应进行分析。等价荷载法是将地基变形按Winkler地基反力假定等价为作用在地基梁上的荷载[23]，如图3所示。

令等效荷载为r()，根据等效荷载法计算原理

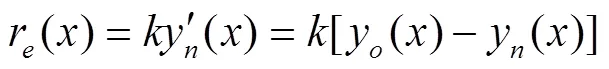
式中y()为计算参考线，可按式（14）进行计算。

注：r()为等效荷载，N·m-1；′()为边坡基土自由相对冻胀线，m；′()为相对计算参考线，m；′()为考虑坡脚约束衬砌板对不均匀冻胀的响应相对冻胀线，m。

Note: r() is the equivalent load, N·m-1;′() is the free relative frost heave line, m;′() is the relative calculation reference line, m;′() is the relative frost heave line of the slope lining slab considering the slope foot constraint and nonuniform frost heave, m.

图3 边坡衬砌板相对冻胀线

Fig.3 Relative frost heaving line of slope lining slab

地基的变形由于受到各种复杂因素的影响，具有多样性和复杂性，而并不是所有位移模式下的弹性地基梁都有显式解析解。只有少数几种位移模式具有显式解析解，如指数曲线等。而大多数位移曲线模式只能通过数值叠加、级数展开等近似方法求解[23]。

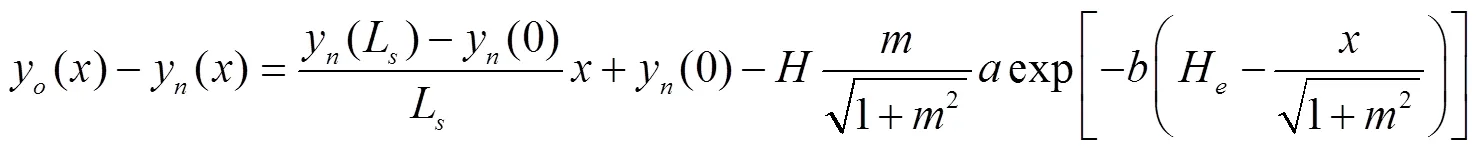
由式（15）可以看出y()−y()为复合函数，因此对其采用级数展开进行近似求解。通过勒让德多项式对y()−y()函数进行三次最佳平方逼近[24]可近似得到

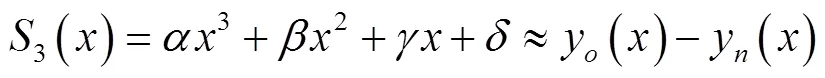
式中3()为y()−y()的三次最佳平方逼近方程；、、和为多项式系数。

则r()可近似按下式计算

如图2d所示，在考虑坡脚约束和基土不均匀冻胀情况下，边坡衬砌板的边界条件为

1）当=0时，M(0)=0，V(0)=0；

2）当=L时，M(L)=0，V(L)=−F；

将以上边界条件代入式（11）和式（12）则有

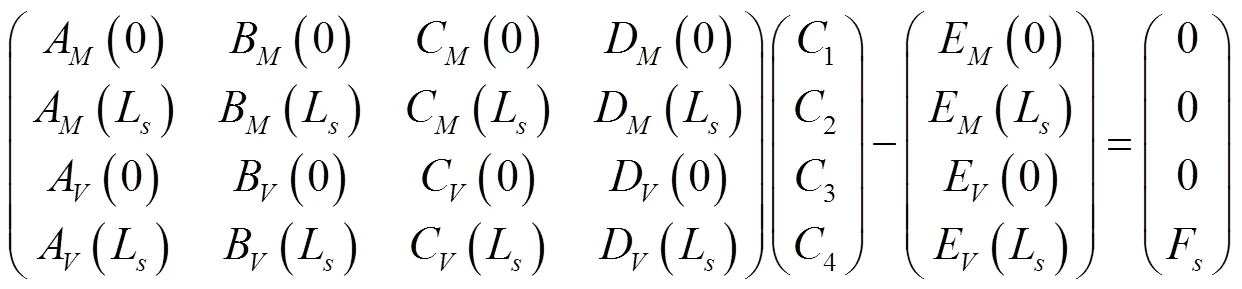
解出1、2、3和4，并代入式（6）～式（8）便可得到边坡衬砌板在冻胀后相对于计算参考线y()的挠度响应y()，弯矩M()和剪力V()。通常研究中更关注相对于冻前地面线的挠度响应，因此边坡衬砌板在基土发生不均匀冻胀的挠度为

不均匀冻胀时的边坡冻胀反力p()为

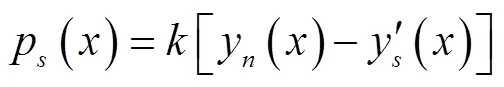
2.3 计算流程

1）根据现场观测或相关文献[1-4]确定式（2）中系数和；

2）将式（1）代入式（2），再将式（2）代入式（3）～式（5）确定边坡基土的y()、y()和y()；

3）根据式（13）～（17）确定边坡衬砌板在发生不均匀冻胀时的等效荷载r()；

4）将计算出的等效荷载r()代入式（18），得到含F的积分常数1、2、3和4；

5）将积分常数1、2、3和4代入式（6），并令y(L)=y(L)，解出F；

6）将F代入1、2、3和4，解出各积分常数值，再将1、2、3和4代入式（6）～式（8），得到边坡衬砌板在冻胀后相对于计算参考线y()的挠度响应y()，弯矩M()和剪力V()。

7）将y()代入式（19），再将式（19）代入式（20），便可得到y′()和p()。

3 案例研究与结果分析

文献[9]与前人的试验[25]和数值模拟[26]进行对比，系统地论证了基于基土自然冻胀位移的弹性地基梁理论在渠道冻胀过程受力分析中的可行性和优越性，但文献[9]仅考虑基土在均匀冻胀情况下渠道衬砌板的冻胀响应，并未讨论基土不均匀冻胀对渠道冻胀过程的影响。文献[3]论述了目前冻胀量和地下水位关系的研究现状，总结了不同地区、不同土壤冻胀量和地下水位的关系函数。寒区高水位地区渠道的边坡衬砌板下基土距地下水位的距离不同，在自然冻胀过程中，其自然冻胀量呈现不均匀分布。本文基于文献[9]中关于甘肃省靖会总干渠冻胀的相关力学参数和文献[3]中关于甘肃省的高液限土壤自然冻胀率和地下水位的函数关系，探究甘肃省高水位地区梯形渠道衬砌板在基土不均匀冻胀情况下的力学响应，以期为高水位地区的渠道冻胀设计提供参考。

甘肃省某高水位地区的梯形渠道地下水位距地表5 m。渠道边坡系数1.0。该地区土壤为高液限土壤，根据文献[3]，该地区土壤特征系数和（式（2））分别为40和1.25。冻深1.2 m，冻土泊松比0.30，弹性模量46 MPa；采用混凝土材料进行衬砌，衬砌厚度10 cm，其弹性模型为24 GPa[9]。

3.1 基土不均匀冻胀对边坡衬砌板的影响

在实际渠道边坡衬砌板的冻胀过程中，其坡脚处的冻胀量由于渠底衬砌板的存在会产生一定的约束。边坡衬砌板的冻胀过程其实是基土不均匀冻胀和坡底约束共同作用的结果。

将案例参数代入本文力学模型，根据第2.3节计算流程进行计算，其中考虑基土不均匀冻胀和坡脚约束的不同边坡衬砌板长度的计算结果见图4～图6。边坡衬砌板计算结果最大值见表1。

注：空心点为自然冻胀量，实心点为约束冻胀量。

图5 不同边坡衬砌板长度冻胀反力计算结果

图6 不同边坡衬砌板长度弯矩计算结果

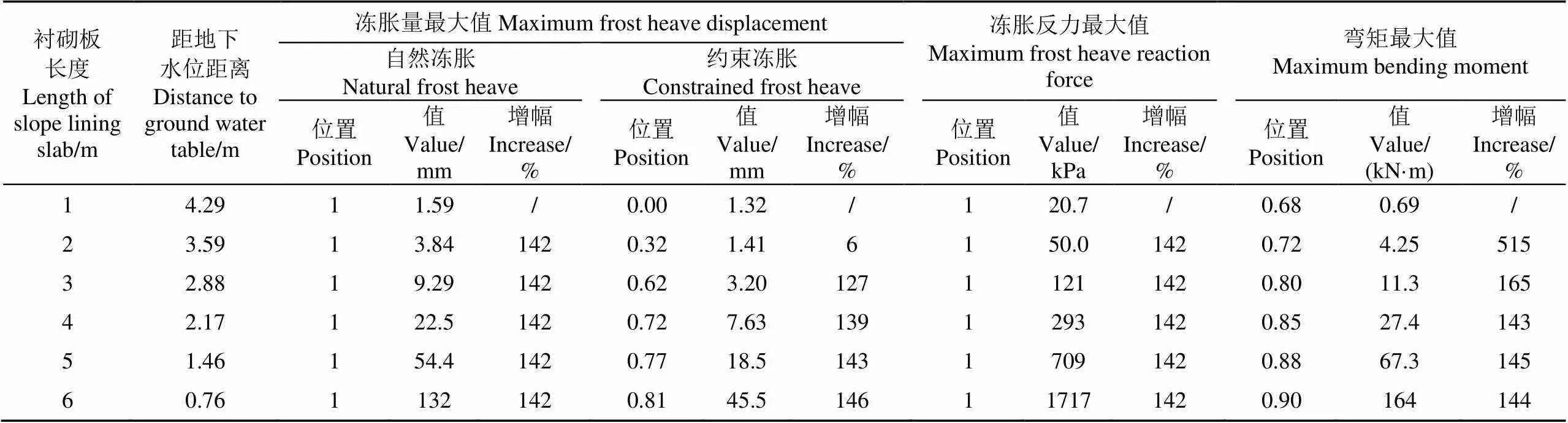
表1 边坡衬砌板计算结果最大值

注：位置为距坡顶的相对长度；增幅为相对于上一个边坡衬砌板长度计算结果的增加百分比。

Note: The position in the table is the relative length from the top of the slope. The increase is the increase percentage relative to the above calculation result of the last lining slab.

1）冻胀量

图4为边坡衬砌板的冻胀量分布图。由图4和表1可以看出在边坡系数和地下水位一定的情况下，边坡衬砌板长度每增加1 m，其自然冻胀量最大值增大142%；其约束冻胀量的最大值增幅逐渐变大；约束冻胀量的最大点位置也由渠顶向下偏移。由1 m增加到2 m时，其增幅最小，仅有6%，这是由于边坡衬砌板相对较短，整体刚度相对较大，边坡衬砌板在底部约束的情况下，其上半部分会出现上翘，但上翘变形产生的法向冻结力不足以使衬砌板上半部分下弯。因此，当边坡衬砌板相对较短时，其约束冻胀量最大值在边坡衬砌板上部区域。当边坡衬砌板相对较长时（L=3～4 m），在坡脚冻胀力的作用下，虽然其上半部分有上翘的趋势，但由于其整体相对刚度相对较小，在法向冻结的作用下，上半部分衬砌板下弯变形，和基土自然变形相互协调适应。

2）冻胀反力

图5为边坡衬砌板的冻胀分力分布图。当衬砌板相对较短时（L=1～2 m），其冻胀反力分布呈现三角分布，和以往的力学模型[10-16]中假设的分布规律基本一致，但随着边坡衬砌板长度的逐渐增加，其冻胀反力主要分布区域向坡脚偏移。随着边坡衬砌板长度每增加1 m，最大冻胀反力值便增大142%，这和边坡衬砌板下的自然冻胀量的最大值增幅和位置相一致，同在坡脚。这是由于边坡衬砌板坡脚处距地下水位最近，使其自然冻胀量最大，但由于渠底衬砌板约束的存在，使该处的自然冻胀量不能完全被释，因此该处产生的冻胀反力也就最大，故坡脚冻胀反力最大值增幅和自然冻胀量最大值增幅相一致。

3）弯矩

图6为边坡衬砌板弯矩分布图。由图6和表1可以看出边坡衬砌板每增加1 m，弯矩最大值增幅分别为515%、165%、143%、145%和144%，弯矩最大值平均增大223%。边坡衬砌板由1 m增大到2 m时其增幅最大，随后的增幅主要在145%左右。在L=1～2 m时弯矩最大值在距坡脚1/3左右处，这是由于冻胀反力分布接近三角分布，因此其弯矩最大值基本在距坡脚1/3左右处位置。随着边坡衬砌板长度逐渐增加（L=3～6 m），渠基土不均匀冻胀程度愈加明显，在坡脚附近冻胀反力相对偏大，使弯矩最大值点向坡脚偏移。同时由于基土自然冻胀的“内凹”趋势存在，加上衬砌板相对较长，其整体刚度相对较小，使得在边坡衬砌板的上半部分产生一定的负弯矩（L=4～6 m）。由于该负弯矩的存在，又进一步加剧弯矩最大值点向坡脚的偏移。

3.2 基土不均匀冻胀和均匀冻胀计算结果对比

以边坡衬砌板长度为4 m为例，探究不均匀冻胀和均匀冻胀计算结果上的差异。为了减少自然冻胀量整体上的差异对计算结果的影响，本文计算用不均匀冻胀产生自然冻胀的平均值y（m）来表示均匀冻胀的自然冻胀量，可按下式进行计算：

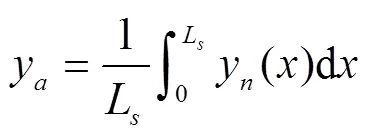
式中L为边坡衬砌板长度，m；y()为边坡衬砌板下基土法向自然冻胀量，m。

基土均匀冻胀对边坡衬砌板的影响按文献[9]进行计算，不均匀冻胀按本文计算，其计算结果如图7所示。由图7可以看出均匀冻胀和不均匀冻胀的计算结果存在着较大的差异。不均匀冻胀的计算结果明显比均匀冻胀的偏大。

均匀冻胀的约束冻胀量最大值为6.6 mm，不均匀冻胀的为7.6 mm，比均匀冻胀大了15.2%。在分布规律上相差较大，均匀冻胀由于在渠道上半部分存在一定的自然冻胀量，加之外部约束相对较弱，因此，在上半部分的约束冻胀量相对较大；不均匀冻胀的自然冻胀量在边坡上半部分相对较弱。由于法向冻结力的存在，使得边坡衬砌板向下一定弯曲，因此不均匀冻胀的在渠道上半部分的约束冻胀量相对较弱。

由图7b和图7c可以看出不均匀冻胀产生的冻胀反力和弯矩明显比均匀冻胀的大的多。冻胀反力最大值，不均匀冻胀比均匀冻胀大264%；弯矩最大值，不均匀冻胀计算结果比均匀冻胀大170%。这是由于不均冻胀在坡脚处被约束的自然冻胀量较大，因此该处的冻胀反力和弯矩也相对较大。

因此，在寒区高水位地区进行渠道抗冻胀设计时，如果按均匀冻胀进行分析计算，那么设计结果可能存在一定的安全隐患。

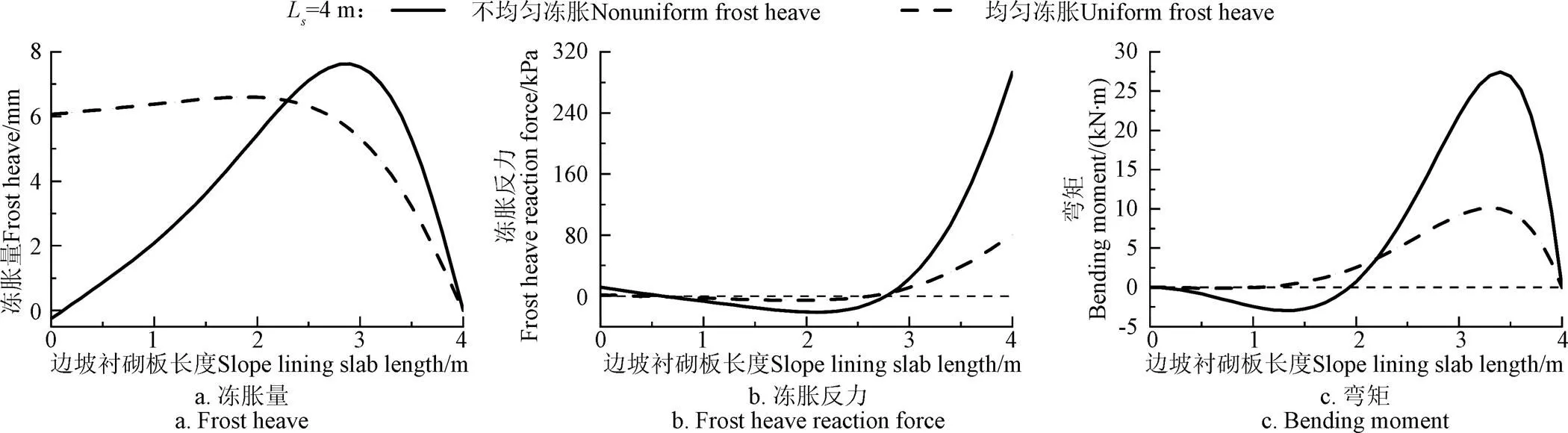
图7 边坡基土均匀与不均匀冻胀结果对比图

4 结 论

1）本文将渠道衬砌板与基土相互作用效应分解为基土不均匀自由冻胀位移、衬砌板受到冻土反作用产生的位移和边坡衬砌板坡脚约束产生的相对转动位移，从而建立了满足两端变形协调的弹性地基梁模型。

2）以甘肃省高液限土壤地下水位5 m地区的边坡系数为1 的渠道为例，探究不同边坡衬砌板长度在冻胀过程对变形和内力影响规律。结果表明边坡衬砌板每增加1.0 m，边坡衬砌板坡脚处的冻胀反力最大值会增大142%，弯矩最大值平均增大223%。同时弯矩最大值点会从原来的距坡脚1/3 左右处向坡脚偏移。因此，在寒区的高水位地区宜采用宽浅式横断面。对于窄深式横断面梯形渠道，建议在距坡角1/3～1/5的边坡衬砌板长度范围内设置分缝用于释放冻胀力，其具体位置宜根据地下水位、边坡衬砌板长度和边坡系数来进行综合考虑确定。

3）以边坡衬砌板长度为4 m为例，探究基土均匀冻胀和不均匀冻胀对边坡衬砌板影响的差异，得出基土不均匀冻胀的冻胀反力最大值和弯矩最大值，分别比基土均匀冻胀大264%和170%。

本文将渠道基土和衬砌板看为完全弹性体，而忽略基土冻胀过程塑性变形和衬砌板开裂破坏对其结果的影响，因此本文模型计算结果值比实际结果偏大，考虑渠道基土在冻胀过程的塑性变形和衬砌开裂破坏，仍有待进一步研究。

[1] 郭富强，史海滨，程满金，等. 不同地下水位下渠基冻胀规律与保温板适宜厚度确定[J]. 农业工程学报，2018，34(19)：95-103. Guo Fuqiang, Shi Haibin, Cheng Manjin, et al. Law of frost heave of canal foundation and appropriate thickness of insulation board under different groundwater levels[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 95-103. (in Chinese with English abstract)

[2] 朱强，付思宁，武福学，等. 论季节冻土的冻胀沿冻深分布[J]. 冰川冻土，1988，10(1)：1-7. Zhu Qiang, Fu Sining, Wu Fuxue, et al. On the frost heave distribution along depth[J]. Journal of Glaciology and Geocryology, 1988, 10(1): 1-7. (in Chinese with English abstract)

[3] 卞晓琳，何平，施烨辉. 土体冻胀与地下水关系的研究进展[J]. 中国农村水利水电，2007(4)：24-27. Bian Xiaolin, He Ping, Shi Yehui. Research progress on the relationship between soil freezing and groundwater[J]. China Rural Water and Hydropower, 2007(4): 24-27. (in Chinese with English abstract)

[4] 王希尧. 不同地下水埋深和不同土壤条件下的冻结和冻胀试验研究[J]. 冰川冻土，1980，3(2)：40-45. Wang Xiyao. Experimental research of frost heave under different level of groundwater in various soils[J]. Journal of Glaciology and Geocryology, 1980, 3(2): 40-45. (in Chinese with English abstract)

[5] 中华人民共和国水利部. 渠系工程抗冻胀设计规范，SL 23－2006[S]. 北京：中国水利水电出版社，2006：9.

[6] 塞尔瓦杜雷A.P.S. 土与基础相互作用的弹性分析[M]. 北京：中国铁道出版社，1984.

[7] 郭继武. 地基基础设计简明手册[M]. 北京：机械工业出版社，2007.

[8] 肖旻，王正中，刘铨鸿，等. 考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型[J]. 水利学报，2017，48(10)：1229-1239. Xiao Min, Wang Zhengzhong, Liu Quanhong, et al. Elastic foundation beam model of frost heave damage of trapezoidal canal considering interaction between frozen soil and lining structure[J]. Journal of Hydraulic Engineering, 2017, 48(10): 1229-1239. (in Chinese with English abstract)

[9] 李宗利，姚希望，杨乐，等. 基于弹性地基梁理论的梯形渠道混凝土衬砌冻胀力学模型[J]. 农业工程学报，2019，35(15)：110-118. Li Zongli, Yao Xiwang, Yang Le, et al. Mechanical model of frost heaving of concrete lining trapezoidal canal based on elastic foundation beam theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 110-118. (in Chinese with English abstract)

[10] 王正中. 梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2004，20(3)：24-29. Wang Zhengzhong. Establishment and application of mechanics model of frost heaving damage of concrete lining trapezoidal open canal[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(3): 24-29. (in Chinese with English abstract)

[11] 王正中，李甲林，陈涛，等. 弧底梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2008，24(1)：18-23. Wang Zhengzhong, Li Jialin, Chen Tao, et al. Mechanics models of frost-heaving damage of concrete lining trapezoidal canal with arc-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(1): 18-23. (in Chinese with English abstract)

[12] 申向东，张玉佩，王丽萍. 混凝土预制板衬砌梯形断面渠道的冻胀破坏受力分析[J]. 农业工程学报，2012，28(16)：80-85. Shen Xiangdong, Zhang Yupei, Wang Liping. Stress analysis of frost heave for precast concrete panel lining trapezoidal cross-section channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(16): 80-85. (in Chinese with English abstract)

[13] 宋玲，欧阳辉，余书超. 混凝土防渗渠道冬季输水运行中冻胀与抗冻胀力验算[J]. 农业工程学报，2015，31(18)：114-120. Song Ling, Ouyang Hui, Yu Shuchao. Frozen heaving and capacity of frozen heaving resistance of trapezoidal concrete lining canal with water in winter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 114-120. (in Chinese with English abstract)

[14] 李翠玲，王红雨. 两拼式U形渠道混凝土衬砌结构冻胀破坏力学模型[J]. 中国农村水利水电，2014(5)：86-93. Li Cuiling, Wang Hongyu. Mechanics model of frost-heaving damage of concrete lining U-shaped canals with splicing two arc-plates[J]. China Rural Water and Hydropower, 2014(5): 86-93. (in Chinese with English abstract)

[15] 王江伟，王红雨. 考虑土与板间摩擦力的两拼式U形复合衬砌渠道冻胀破坏力学模型[J]. 中国农村水利水电，2016(5)：145-149. Wang Jiangwei, Wang Hongyu. Frost heaving mechanics model of composite lining U-shaped canals considering interface friction from soil, geo-membrane and splicing double arc-plates[J]. China Rural Water and Hydropower, 2016(5): 145-149. (in Chinese with English abstract)

[16] 唐少容，王红雨. 三板拼接式小型U形混凝土衬砌渠道冻胀破坏力学模型[J]. 农业工程学报，2016，32(11)：159-166. Tang Shaorong, Wang Hongyu. Mechanical model of small U-shaped concrete lining canal with three arc-plates under frost heaving[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(11): 159-166. (in Chinese with English abstract)

[17] 郑永来，韩文星，童琪华，等. 软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究[J]. 岩石力学与工程学报，2005，24(24)：4552-4558. Zheng Yonglai, Han Wenxing, Tong Qihua, et al. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4552-4558. (in Chinese with English abstract)

[18] 狄宏规，周顺华，宫全美，等. 软土地区地铁隧道不均匀沉降特征及分区控制[J]. 岩土工程学报，2015，37(S2)：74-79. Di Honggui, Zhou Shunhua, Gong Quanmei, et al. Differential settlement of metro tunnels and its zonal control in soft deposits[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 74-79. (in Chinese with English abstract)

[19] 黄继辉，夏才初，韩常领，等. 考虑围岩不均匀冻胀的寒区隧道冻胀力解析解[J]. 岩石力学与工程学报，2015，34(S2)：3766-3774. Huang Jihui, Xia Caichu, Han Changling, et al. Analytic solution of freezing force of tunnel in cold zone considering uneven frost heaving of surrounding rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 3766-3774. (in Chinese with English abstract)

[20] 刘波，杨伟红，张功，等. 基于隧道不均匀变形的地表沉降随机介质理论预测模型[J]. 岩石力学与工程学报，2018，37(8)：1943-1952. Liu Bo, Yang Weihong, Zhang Gong, et al. A prediction model of stochastic medium theory for ground surface settlement induced by non-uniform tunnel deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(8): 1943-1952. (in Chinese with English abstract)

[21] 马巍，王大雁. 冻土力学[M]. 北京：科学出版社，2017.

[22] 郑秀清，樊贵盛，邢述彦. 水分在季节性非饱和冻融土壤中的运动[M]. 北京：地质出版社，2002.

[23] 廖少明，白廷辉，彭芳乐，等. 盾构隧道纵向沉降模式及其结构响应[J]. 地下空间与工程学报，2006，2(4)： 566-570.

Liao Shaoming, Bai Tinghui, Peng Fangle, et al. Longitudinal settlement forms and structural response of shield tunnel[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(4): 566-570. (in Chinese with English abstract)

[24] 李庆扬，王能超，易大义. 数值分析（第5版）[M]. 北京：清华大学出版社，2008.

[25] 李安国，陈瑞杰，杜应吉，等. 渠道冻胀模拟试验及衬砌结构受力分析[J]. 防渗技术，2000，6(1)：5-16.Li Anguo, Chen Ruijie, Du Yingji. Simulation test of canal frost heave and stress analysis of lining structure[J]. Technology of Seepage Control, 2000, 6(1): 5-16. (in Chinese with English abstract)

[26] 李爽，王正中，高兰兰，等. 考虑混凝土衬砌板与冻土接触非线性的渠道冻胀数值模拟[J]. 水利学报，2014，45(4)：497-503. Li Shuang, Wang Zhengzhong, Gao Lanlan, et al. Numerical simulation of canal frost heaving considering nonlinear contact between concrete lining board and soil[J]. Journal of Hydraulic Engineering, 2014, 45(4): 497-503. (in Chinese with English abstract)

Frost heave mechanical model of concrete lining trapezoidal canal considering nonuniform frost heave of foundation soil based on elastic foundation beam theory

Li Zongli1,2, Yao Xiwang1, Zhang Rui1, Shao Huajian1, Wang Zhengzhong1,2

(1.,,712100,; 2.,,712100,)

In areas with high groundwater levels in cold regions, due to the different distances between the calculation points of the canal slope lining slab and the groundwater level, the frost heave of the foundation soil under the slope lining slab presents a different distribution from the canal top to the canal bottom. The slope lining slab has a large amount of frost heave in the bottom area of the canal, and a small amount of frost heave in the canal top area. To explore the effect of nonuniform frost heave of foundation soil caused by high groundwater level in cold areas on the frost heave of concrete lining trapezoidal cannal, the interaction effect between the lining slab and the foundation soil was disintegrated into the uneven free frost heave displacement of the foundation soil, the displacement produced by the reaction of the lining slab and frozen soil, and the relative rotational displacement of the slope lining slab produced by the restraint of the slope foot. Thus, an elastic foundation beam model that satisfied the coordination of deformation at both ends was established based on the elastic foundation beam model proposed earlier. Taking the canal with slope coefficient of 1 and groundwater level of 5 m as an example, this canal was surrounded by the high liquid limit soil in the Gansu Province. The interaction between the different lengths of slope lining slabs and the nonuniform frost heave foundation soil in the process of frost heave was explored. The results showed that for every 1-m increase in the length of the slope lining slab, the maximum value of frost heave reaction force at the slope foot increased by 142%, and the maximum value of bending moment averagely increased by 223%. Meanwhile, the position of the maximum value of the bending moment moved from the original one-third of the slope foot to the slope foot. Therefore, it was recommended that the cross section should better be designed as wide and shallow as possible in order to reduce the influence of nonuniform frost heave of the foundation soil caused by the groundwater level on the canal lining slabs. For trapezoidal canal with narrow and deep cross-sections, it was recommended to set joints within one-third to one-fifth of the length of the slope lining slab from the slope foot to release the frost heave force. The specific location should be comprehensively considered and determined according to the groundwater level, the length of the slope lining slab and the slope coefficient. Meanwhile, taking the slope lining slab length of 4 m as an example, the difference between the effects of nonuniform frost heave and uniform frost heave on the slope lining slab was explored, and maximum frost heave reaction force and maximum bending moments were 264% and 170% greater than the uniform frost heave of the foundation soil, respectively. Therefore, when designing the anti-freeze-heave canal lining slabs in the cold area with high groundwater, the calculation should be based on the nonuniform frost heave elastic foundation beam model. This study can guide the design of anti-frost heave of canal lining slabs in cold areas with high groundwater.

canals; models; concrete; nonuniform frost heave; frost heave; elastic foundation beam; frozen soil engineering

李宗利，姚希望，张 锐，等. 考虑基土不均匀冻胀的梯形渠道混凝土衬砌弹性地基梁力学模型[J]. 农业工程学报，2020，36(21)：114-121. doi：10.11975/j.issn.1002-6819.2020.21.014 http://www.tcsae.org

Li Zongli, Yao Xiwang, Zhang Rui, et al. Frost heave mechanical model of concrete lining trapezoidal canal considering nonuniform frost heave of foundation soil based on elastic foundation beam theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 114-121. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.21.014 http://www.tcsae.org

2020-06-02

2020-10-01

国家重点研发计划“高寒地区长距离供水工程能力提升与安全保障技术”（2017YFC0405101-2）

李宗利，教授，博士生导师，主要从事水工结构设计理论与材料方面研究。Email：bene@nwsuaf.edu.cn

10.11975/j.issn.1002-6819.2020.21.014

TU445; TV91

A

1002-6819(2020)-21-0114-08