一类微分差分可积方程的新精确解
2021-01-14陈守婷高恒李琪
陈守婷,高恒,李琪
(1 徐州工程学院数学与统计学院,江苏 徐州 221018;2 东华理工大学数学系,江西 抚州 344000)
孤立子理论是非线性科学中的一个热点内容,是推动非线性科学发展的重要理论之一。孤立子理论的发展对数学和物理都具有重要意义,在物理领域,孤立子理论被用来解释许多长期用经典理论未能得到解答的问题,并在流体力学、非线性光学、光纤通讯等众多领域都有着重要的应用,另外,在数学领域,孤立子理论的研究对许多分支及交叉学科的发展有着重要影响和促进作用,该理论涉及众多主干数学分支,而这些数学分支的进一步拓展又成为孤立子理论的理论支持。
孤立子理论目前已经形成了自己独具特色的研究方法,每一种方法又都产生了相应的一系列数学理论体系,其中,寻找孤立子方程的精确解是孤立子理论中非常重要的研究课题之一[1-10]。孤立子理论已经具有许多经典的讨论解的性质和寻求精确解的研究方法,并且这些方法都具有非常丰富的数学理论知识,其中,朗斯基技巧[1-2]作为求解孤立子方程的一种十分有效且简明直接的方法,因其能够直接验证解满足方程的优点,一直得到了众多学者的广泛关注和研究。
朗斯基技巧在被应用于各类非线性发展方程研究求解问题的同时,也得到了诸多变形和推广,其中,双朗斯基[3]是朗斯基的一种推广形式,可以被用来构造双朗斯基行列式解,双Casoratian是双朗斯基的离散形式,被应用于离散系统中的方程求解[4]。SIRIANUNPIBOON S首次给出了KdV方程的广义朗斯基解及有理解[5],基于KdV方程的广义朗斯基解、Positon解、Negaton解、Complextion解及一些其它形式的精确解也陆续被得到[6-7]。陈登远等[8]提出了一种构造双朗斯基行列式元素的矩阵方法,这种双朗斯基行列式元素满足一个含有任意矩阵的方程。利用这种矩阵方法和双朗斯基技巧,AKNS方程的广义双朗斯基解被构造出来,并通过对任意矩阵选取不同的形式得到了有理解、Matveev解、Complexiton解以及混合解,之后这种构造具有双朗斯基行列式形式的多种精确解的矩阵方法被应用于连续和离散系统的多个方程中[11-22]。
受陈登远等[8]研究的启发,ZHANG J P等[14]构造了著名的Ablowitz-Ladik (AL)链的一个微分差分可积方程[23](简称AL方程)
Qn,t=Qn+1(1-QnRn),Rn,t=-Rn-1(1-QnRn)
(1)
的类有理解,其中,{Qn,Rn}是关于变量n的二个位势。本文在文献[14]的基础上,利用双Casoratian技巧和矩阵方法,构造AL方程(1)的新精确解,即具有双Casorati行列式形式的Matveev解及其混合解。
1 广义双Casoratian解
本文参照文献[14-15]构造AL方程(1)的广义双Casoratian解和类有理解。首先从方程(1)的位势变换
(2)
出发,推导出双线性导数方程为
(eDn-1)fn·fn=-gnhn,
(3)
Dtgn·fn=gn+1fn-1,
(4)
Dthn·fn=-hn-1fn+1,
(5)
进而得到该方程的广义双Casoratian解
(6)
式(6)中行列式的列向量Φn和Ψn满足
(7)
(8)
式(8)中C=(c1,c2,…,cN+M)T和D=(d1,d2,…,dN+M)T是二个任意的实常向量。
本文规定
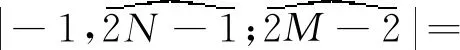
其中E是平移算子,定义为Esu(n)=u(n+s),s∈Z。为方便起见,在不引起混淆的情况下,记u(n)=un,于是,将式(6)代入位势变换式(2),得到AL方程(1)的广义双Casoratian解,进而将式(7)、(8)中的矩阵B取成一种下三角阵的形式,得到方程(1)的类有理解。
2 Matveev解
在广义双Casoratian解(6)的基础上,通过将矩阵B设成Jordan阵,利用构造双Casorati行列式元素的矩阵方法,根据式(7)、(8)中向量Φn和Ψn所对应的的分量,推导满足双线性导数方程(3)~(5)的具有双Casorati行列式形式的新精确解,将所得到的解代入到位势变换(2),进一步给出AL方程(1)的Matveev解。
假设B是(N+M)×(N+M)阶的Jordan矩阵
(9)
不失一般性,考虑其中一个Jordan块 (去掉k的下标)有
其中Il表示l×l单位矩阵。显然有
Js(k)=(kIl+Yl)s=
于是,对任意的正整数s成立
J(k)s=T(k)ks,
用J(k)取代式(7)和(8)中的B,可得
(10)
其分量的形式为
(11)
(12)
令c1=d1=1,cj=dj=0 (j=2,3,…,l),式(11)、(12)可以被简化为
(13)
(14)
如果设
Φn=(φ1n(k1),…,φl1n(k1);φ1n(k2),…,φl2n(k2);…;φ1n(ks),…,φlsn(ks))T;
Ψn=(ψ1n(k1),…,ψl1n(k1);ψ1n(k2),…,ψl2n(k2);…;ψ1n(ks),…,ψlsn(ks))T(l1+l2+…+ls=N+M),
其中
(15)
(16)
于是,由上述向量Φn和Ψn的分量构成的双Casorati行列式为
(17)
式(17)即为AL方程(1)的Matveev解。
假设(N,M)=(1,1),且Φn=(φ1n(k),φ2n(k))T,Ψn=(ψ1n(k),ψ2n(k))T,这里φjn(k)和ψjn(k)表示为式 (13)、(14),则可以算出
将其代入(6)算出
-2(n+te2k),
(18)
可类似算出
(19)
2e-2nk-te2k。
(20)
将式(18)、(19)、(20)代入位势变换(2),得到方程(1)的Matveev解
(21)
不难证明式(21)满足方程(1)。
假设
Φn=(φ1n(k),φ2n(k),φ3n(k))T,
Ψn=(ψ1n(k),ψ2n(k),ψ3n(k))T,
其中,
当(N,M)=(2,1)时,算出
(22)
其中γ=nk+te2k/2。
当(N,M)=(1,2)时,类似可得
(23)
假设
Φn=(φ1n(k1),φ2n(k1),φ1n(k2))T,
Ψn=(ψ1n(k1),ψ2n(k1),ψ1n(k2))T,
这里φjn(kp)和ψjn(kp)(j,p=1,2)表示为式(15)、(16),可算出
当(N,M)=(2,1)时可算得
Qn=
(24)
Rn=
(25)
其中γs=nks+te2ks/2,s=1,2。
类似地,当(N,M)=(1,2)时可算得
Qn=
(26)
Rn=
(27)
容易验证式(22)至(27)同样满足方程(1),也是方程(1)的Matveev解,验证过程本文不做赘述。
3 混合解
假设矩阵B是由下三角阵Br和Jordan阵Bm(9)构成的准对角线矩阵,即
将Φn和Ψn设为
Φn=(ΦrnT,ΦmnT)T,Ψn=(ΨrnT,ΨmnT)T,
(28)
式(28)中,Φrn、Ψrn所满足的条件和分量值见文献[14],Φmn、Ψmn的分量满足式(13)、(14),且
EΦsn=AΦsn,
E-1Ψsn=AΨsn,
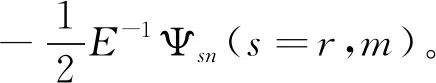
显然,以式(28)列向量构成的双Casorati行列式(17)也是方程(1)的解,将它称为AL方程(1)的类有理解和Matveev解的混合解。
假设
Φn=(φ1,rn,φ2,rn,φmn(k))T,
Ψn=(ψ1,rn,ψ2,rn,ψmn(k))T,
当(N,M)=(2,1)时可以得到
2(n+t)eγ+2k-2(n+t+1)eγ+2e-γ+t,
(29)
2eγ+3k+t-4eγ+k+t+2eγ-k+t,
(30)
2(n+t)e-γ-k-2(n+t+1)e-γ+k+2eγ+k-t。
(31)
将式(29)~(31)代入位势变换(2),算得方程(1)的解为
(32)
当(N,M)=(1,2)时,可以算出
(33)
式(32)、(33)即为方程(1)的类有理解和Matveev解的混合解。
假设Φn=(φ1,rn,φ2,rn,φ1,mn,φ2,mn)T,Ψn=(ψ1,rn,ψ2,rn,ψ1,mn,ψ2,mn)T,当(N,M)=(2,2)时,计算得到以下各式:
fn=4(t2+nt+t)e4k+4(n2-nt+2n-2t2-t+1)e2k+4(n2+nt+2n+t+1)e-2k-4e2γ+2k-t-4e-2γ-2k+t-4(2n2+nt-t2+4n+t),
(34)
gn=-4(n+t)e2γ+4k+8(n+t+1)e2γ+2k-4(n+t+2)e2γ-4te4k+t-4(n-2t+2)e2k+t+4(2n-t+2)et-4ne-2k+t,
(35)
hn=-4(n+t+2)e-2γ+8(n+t+1)e-2γ-2k-4(n+t)e-2γ-4k-4te4k-t-4(n-2t)e2k-t+4(2n-t+2)e-t-4(n+2)e-2k-t。
(36)
再次利用位势变换(2)可得方程(1)的类有理型和Matveev型的混合解,进一步通过选取(N,M)为不同的值,可得方程(1)更多的类有理型和Matveev型的混合解。
4 结论
(1) 本文基于双Casoratian技巧和矩阵方法构造出的Matveev解及其混合解都是AL方程的具有双Casorati行列式形式的新解,这些解丰富了AL方程精确解的类型,为连续和离散系统中的其它方程的求解给出了方向,也为接下来的孤子可积代数特征的教学和研究提供了理论支持。
(2)本文所用的求解方法简便有效,适用于相当一部分非线性发展方程。
