The superpotential and geometric invariants of D-brane system on compact Calabi-Yau manifold*

LI Fei, YANG Fuzhong

(School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)

Abstract The effective D-brane superpotential determines the vacuum structure and is the generating function of the Ooguri-Vafa invariants. It is of great significance in both physics and mathematics. In this work, the superpotential of the system with three D-branes is calculated by mirror symmetry, GKZ-system (hypergeometric system of Gel’fand, Kapranov, and Zelevinski) method, and the type II/F-theory duality. On compact Calabi-Yau manifold, the superpotenial and geometric invariants of D-brane system in the three phases are studied. The calculations show that the superpotentials in the three phases are different. This implies that the enhanced gauge symmetry in low energy theory and geometric singularity may lead to the phase transition.

Keywords superstring; F-theory; superpotential; Ooguri-Vafa invariants

Mirror symmetry gives the equivalence between A-model determined by Kähler moduli of quantum geometry and B-model determined by complex structure moduli of the classical geometry in the topological string theory. Supersymmetry breaks fromN=2 toN=1 when D-brane is included. Correspondingly, open-closed mirror symmetry[1-2]between A and B models is developed. On the analogy of the prepotential inN=2 supersymmetric topological string theory, the counterpart is called the non-perturbed holomorphic superpotential inN=1 supersymmetric topological string theory[3]. In this work, the D-brane superpotential is calculated by mirror symmetry, GKZ-system method, and the type II/F-theory duality[4-8].

Since there is no quantum correction and it is relatively easy to deal with, we calculate the effective superpotential on the side of B-model. Considering that the space-filling D5-branes wrap on a reducible curveC=∑iCiandCis embedded in a divisorDof Calabi-Yau 3-foldM3, the effective superpotential is

γ∈H3(M3,D).

(1)

The effective superpotential[9]can be expressed as a linear combination of relative period[10]:

(2)

On the other hand, the type II string theory is dual to F-theory[11-12]. The D-brane superpotential in type II string theory is dual to the background flux superpotential in F-theory[11]. The D-brane superpotential of type II on a compact Calabi-Yau threefoldM3can be obtained in F-theory which is on a compact Calabi-Yau fourfoldM4. The superpotential of 4-form fluxG4in F-theory compactified on the Calabi-Yau 4-foldM4is a section of the Hodge line bundle in the complex structure moduli spaceMcs(M4). This superpotential is called Gukov-Vafa-Witten superpotential,

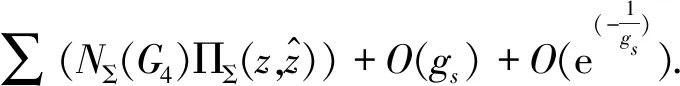
(3)

The leading term on the right-hand side of the above equation is the D-brane superpotentialWN=1, andgsis the string coupling strength.

In the weak coupling limitgs→0, the D-brane superpotentialWNcan be obtained from the GVW superpotentialWGVWof F-theory:

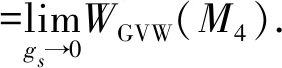
(4)

The system with three D-branes is more complex than the system with single or two D-branes. Complicated D-brane systems play the important role in the phenomenological applications such as superstring/ M/F-theory for MSSM. In this work, for the system with three D-branes on the hypersurface P(1,1,1,1,2), i.e., Sextic, the type II string theory and F-theory duality[12]are used to calculate the D-brane superpotential and Oogrui-Vafa invariants. The phase transitions, the parallel phase→the partial coincident phase→the complete coincident phase, correspond to the enhancement of gauge groupU(1)×U(1)×U(1)→U(1)×U(2)→U(3), in the low energy effective theory.

1 Toric geometry of D-branes system and the generalized hyper-geometric system of Gel’fand, Kapranov, and Zelevinski (GKZ-hypergeomtric system)

(5)

Thenparallel D-branes are defined by reducible divisor:

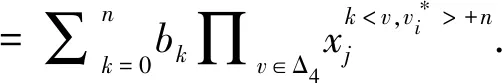
(6)

The parallel D-brane geometry corresponds to the Coulomb phase of the gauge theory and the corresponding group isU(1)×U(1)…U(1)[11,15].

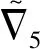
(7)

The gauge groupU(1)×U(1)…U(1) is promoted to theU(N) group when parallel D-branes coincide, while the phase is translated to the Higgs branch.

The bases for choosing compactifying point are given as follows. 1) The origin is to be included in the enhanced polyhedron. 2) The polyhedron and dual polyhedron are convex polyhedron.

The relative period satisfies the differential equations of Picard-Fuchs[16], and its differential operator derived by GKZ-system[4]is

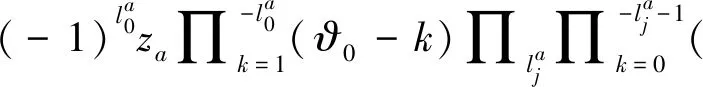
(8)

According to the generators of Mori cone, the local coordinates near the limit point of large complex structure inM4moduli space have the forms

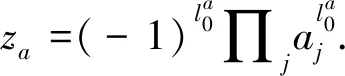
(9)

Mori cone and Kähler cone are dual to each other. The selection of Mori cone generatorlaalso gives a set of dual bases for Kähler cone, denoted asJa∈H(1,1)(W4). The corresponding local coordinate is marked aska. Since the large complex structure limit point is dual to the large radius limit point, thekaof Kähler moduli space are also known as flat coordinates.

Local solution of GKZ-system can be derived from basic cyclew0,

w0(z;ρ)=∑m1,…,ma≥0

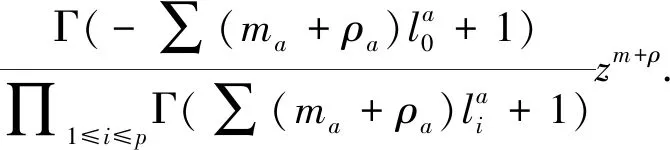
(10)

By using the Frobenius method, the complete cycle vector has the form,

(11)

The mirror conjecture gives the dual periodic vectors on the side of A-model as follows:

(12)

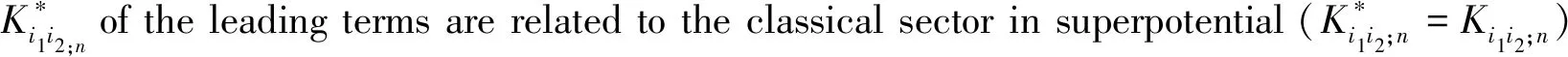
Mirror map is given by

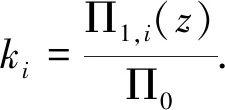
(13)

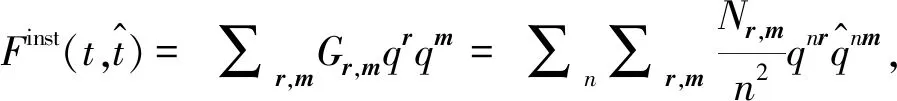
(14)

where {Gr,m} are open Gromov-Witten invariants and {Nr,m} are Ooguri-Vafa invariants.mrepresent the elements ofH1(L) andrrepresent the elements ofH2(W3).

2 Model: D-brane system on the Sextic

The hypersurfaceP(1,1,1,1,2) is given by a polynomial

a0x1x2x3x4x5.

(15)

The degree 6 hypersurfacePis in the ambient toric varietyPΣ(Δ4). The toric variety is determined by the vertices of the polyhedron Δ4as follows:

v1=(2,-1,-1,-1),v2=(-1,5,-1,-1),

v3=(-1,-1,5,-1),v4=(-1,-1,-1,5),

v5=(-1,-1,-1,-1).

2.1 Parallel phase of three D-branes:

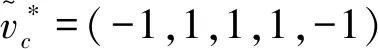
We consider the parallel D-branes defined by the reducible divisorD=D1+D2+D3, which can be written as the degree 15 homogeneous equations,

(16)

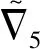
0 1 2 3 4 5 6 7 8 9c

l1=(-4 0 1 1 1 1 -2 2 0 00)

l2=(0 0 0 0 0 0 1 -2 1 00)

l3=(0 0 0 0 0 0 0 1 -21 0).

l4=(-1 1 0 0 0 0 0 0 1-10)

l5=(-3 0 0 0 0 1-2 3 0 0 1)

(17)

A suitable set of bases is selected to visualize the closed and open moduli,

t=k1+2k2+2k3+2k4,

(18)

The leading terms of the relative periods are

(19)

Using algebraic coordinates as follows:

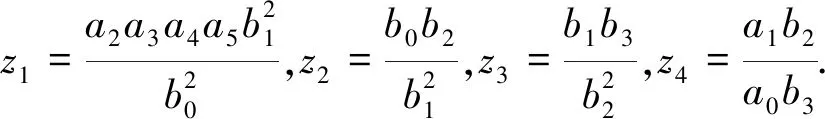
(20)

the fundamental period and the logarithmic period are

Π0(z)=w0(z;0),Π1,i=∂ρi(z;ρ)|ρi=0

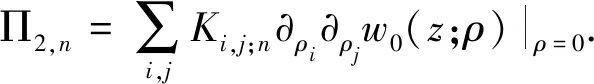
(21)

The flat coordinates are given by

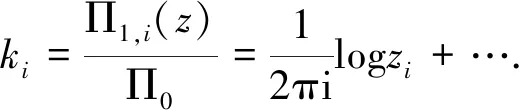
(22)

Then the mixed inverse mirror maps in terms ofqi=exp(2πiki) for {i=1,2,3,4} are

z4=q4+q3q4+q2q3q4+12q1q2q3q4+

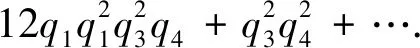
(23)

According to the leading terms, we find the relative periods which correspond to the closed-string period and the D-brane superpotentials in the A-model as follows:

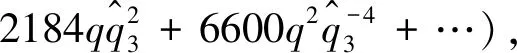
(24)

The disk invariants are shown in Table 1.

Table 1 Ooguri-Vafa invariants Nn1,n2,n3,n4

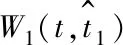
2.2 Partial coincident phase of three D-branes

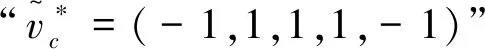
0 1 2 3 4 5 6 7 8c

l1=(-8 0 2 2 2 2-2 2 0 0)

l2=( 0 0 0 0 0 0 1-3 2 0).

l3=(-1 1 0 0 0 0 0 1-1 0)

l4=(-6 0 0 0 0 2-1 30 2)

(25)

A suitable set of bases is selected to visualize the closed and open moduli.

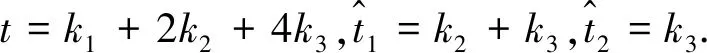
(26)

The leading terms of the relative periods are:

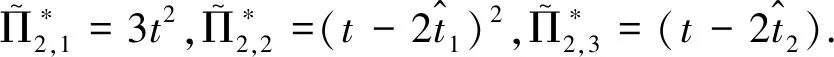
(27)

Using algebraic coordinate:

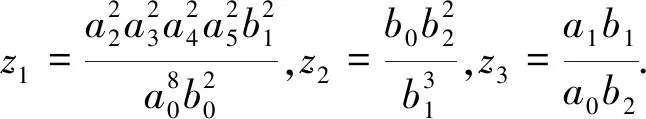
(28)

Then the mixed inverse mirror maps in terms ofqi=exp(2πiki) for {i=1,2,3} are:

2520q1q2q3+….

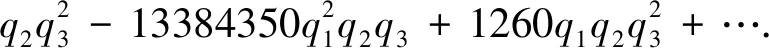
(29)

D-brane superpotentials in the A-model as follows:

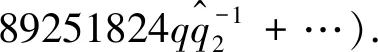
(30)

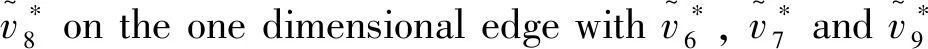
0 1 2 3 4 5 6 7 8c

l1=(-4 0 1 1 1 1-2 2 0 0)

l2=( 0 0 0 0 0 0 2-3 1 0).

l3=(-2 2 0 0 0 0 0 1-1 0)

l4=(-3 0 0 0 0 1-2 3 0 1)

(31)

A suitable set of bases is selected to visualize the closed and open moduli.

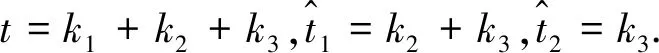
(32)

The leading terms of the relative periods are:

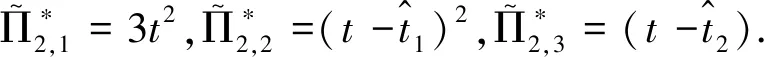
(33)

Using algebraic coordinate:

(34)

Then the mixed inverse mirror maps in terms ofqi=exp(2πiki) for {i=1,2,3} are:

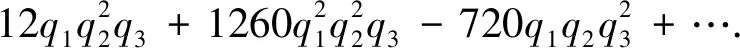
(35)

D-brane superpotentials in the A-model as follows:

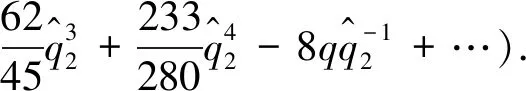
(36)

2.3 Complete coincident phase of three D-brane

0 1 2 3 4 5 6 7c

l1=(-12 0 3 3 3 3-2 2 0)

l2=(-3 3 0 0 0 0 1 -1 0).

l3=(-3 0 0 0 0 1 0 1 1)

(37)

A suitable set of bases is selected to visualize the closed and open moduli.

(38)

The leading terms of the relative periods are

(39)

Using algebraic coordinate:

(40)

Then the mixed inverse mirror maps in terms ofqi=exp(2πiki) for {i=1,2} are

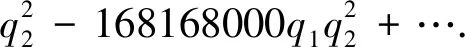
(41)

D-brane superpotentials in the A-model as follows:

(42)

The disk invariants are shown in Table 2.

3 Summary

The superpotential and Ooguri-Vafa invariants of D-brane system with three D-branes on hypersurfaceP(1,1,1,1,2), i.e., Sextic are calculated. Different from previous works on the systems with single and two D-branes, the system with three D-branes complicates the research.

The results show that there are three phases: parallel phase, partial coincident phase and complete coincident phase. The parallel phase of the D-brane system corresponds to the Coulomb branch of gauge theory, and the superpotential contributed by one of the three D-branes is identical to the one contributed by the D-brane system with single brane on the same Calabi-Yau manifold. The partial coincident phase of the D-brane system corresponds to the Coulomb-Higgs branch. The D-brane system changes from parallel D-brane phase to partial coincident D-brane phase, and that corresponds to the transition from theU(1)×U(1)×U(1) toU(1)×U(2) in terms of gauge theory. The complete coincident phase of the D-brane system corresponds to the Higgs branch. The D-brane system changes from parallel D-brane phase to complete coincident D-brane phase, and that shows the feature of the phase transition fromU(1)×U(1)×U(1) toU(3) in terms of gauge theory.

Therefore, in the low effective theory of the system with three D-branes on compact Calabi-Yau manifolds, the superpotentials have rich phase structures. On the other hand, these superpotentials have potential phenomenological applications. We also try to calculate the D-brane superpotential with the method ofA∞structure and derived category approach and path algebras of quivers.