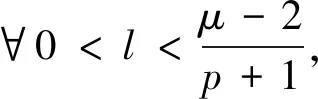一类带有奇异位势的强奇性偏微分方程的正解的性质*

唐露，双震，孙义静

(中国科学院大学数学科学学院， 北京 100049)

本文研究如下带有奇异位势的矩阵型强奇异偏微分方程

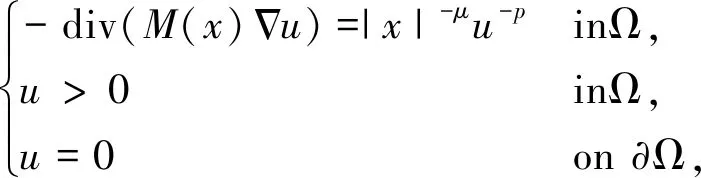
(1)

1 本文主要研究成果

众所周知(参见文献[7])，如下问题：

定理1.1设Ω是n(n≥3)中包含原点的具有光滑边界的有界开集,M(x)是定义在Ω上的实对称矩阵，满足：存在正常数α,β使得M(x)ξ·ξ≥α|ξ|2,|detM(x)|≤β,∀ξ∈n,∀x∈Ω,-3<-p<-1,-n<-μ<0, 则方程

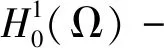
定理1.2设Ω是n(n≥3)中包含原点的具有光滑边界的有界开集,M(x)是定义在Ω上的实对称矩阵，满足：存在正常数α,β使得则方程(1)的任一解u无界，即u∉L∞(Ω)。

定理1.3设Ω是n(n≥3)中包含原点的具有光滑边界的有界开集, -3<-p<-1, 如果-n<-μ<-2, 则方程

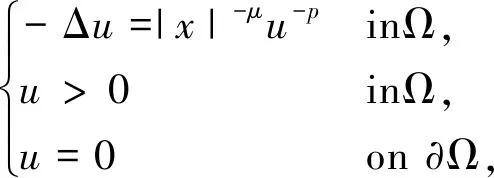
(2)

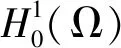
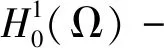
2 定理1.2的证明

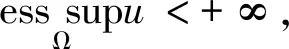
其中β=(β1,β2,…,βn)为多元指标，|β|=β1+…+βn,c(n,|β|)是与n,β有关的正参数，特别地，

由于u是方程(1)的解，有

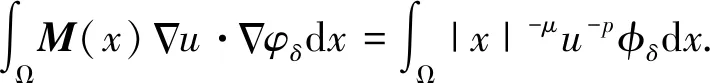
(3)

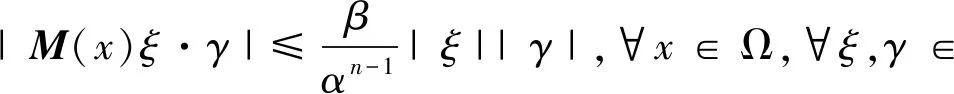
其中c1是与α,β,n有关、与δ无关的正数值。估计(3)右边值，有

其中c2是与α,β,n有关、与δ无关的正数值。于是得到

即

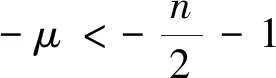
3 定理1.3的证明

用反证法证明。假设方程(2)的C2(Ω{0})-解u不满足性质

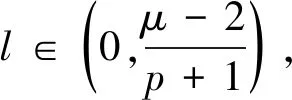
-Δu≡|x|-μu-p,∀x∈Ω{0}.

(4)

令R=r2-n, 定义区域

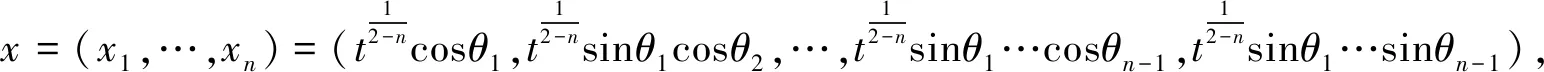
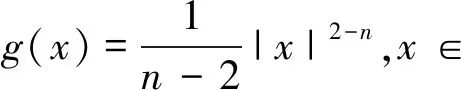
=-x|x|-n,∀x∈Ω(t),

Δg(x)=0,∀x∈Ω(t).

由格林恒等式，有

即

计算A(t)的一阶导数，

在Γ(t)中，有

则

上述等式最后一步根据散度定理而来。计算A(t)的二阶导数，有

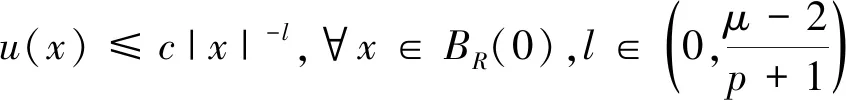
我们来估算A(t),A″(t)。

其中d1,d2,d3是与n,μ,p有关、与t无关的正数值。从而，得到关系式

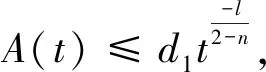
(5)

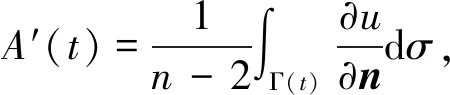
(6)

(7)

下面分析当t→∞,A(t),A′(t),A″(t)可能出现的情况。由A″(t)<0, 可知A′(t)单减：

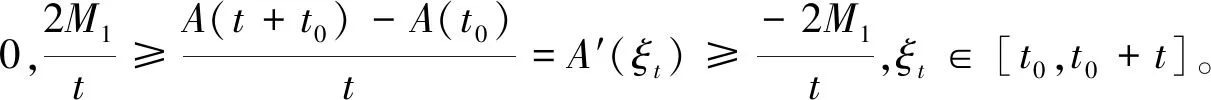
定义函数F(t)

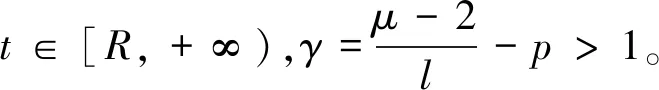
F′(t)=A(t)-γ·A′(t),

F″(t)=A(t)-γA″(t)-γA(t)-γ-1A′(t).

已知A′(t)≥0, 且由式(5)，有

F″(t)≤A(t)-γA″(t)

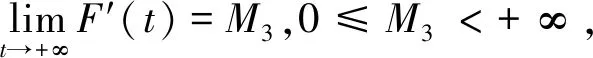
考虑函数sF″(s),s∈[R,t], 它的积分满足

则有

-RF′(R)-F(t)≤-d4(lnt-lnR).