浅谈直流电路中的动态分析问题
2021-01-13林志明

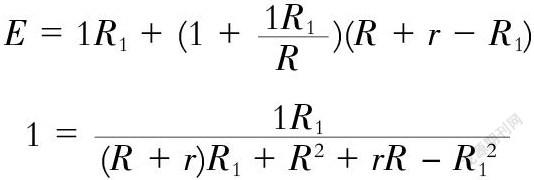
【摘 要】 直流电路中的动态分析问题介绍“电路的动态变化”模型指电路中的局部电路变化时引起的电流或电压的变化,变化起因有变阻器、电键的闭合与断开、变压器变匝数等。面对这类问题,学生的判断缺少灵活性,常常错误率较高。一般来说,解决这类问题时,应当利用闭合电路的欧姆定律,将待分析部分的电路的参数,如电压、电流、功率等的变化情况,和电路中发生变化部分的电阻的变化情况联系起来,进而得到电流、电压、功率等的变化情况。
【关键词】 等效电路 动态变化 串反并同
例如:
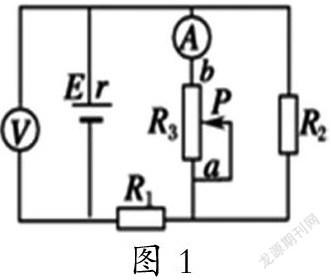
如图所示,电路中电源的电动势为E,内阻为r,R1和R2是定值电阻,求当变阻器R3的滑动触头P由a端向b端滑动时,电路中理想电流表和电压表的示数变化情况。
一般情况下,应该按照如下分析:当变阻器R3的滑动触头P由a端向b端滑动时,R3变小,总电阻变小。根据闭合电路欧姆定律I=E/(R+r),电路的总电流变大,由U内=Ir可知内电压变大,路端电压U外=E-Ir变小,因此电压表示数变小。电阻R1的电流和电压变大,并联电路的电压U=E-IR1-Ir变小,因此电阻R2和R3两端的电压也变小。通过电阻R2的电流变小,通过电阻R3的电流I3=I-I2变大,因此电流表示数变大。
一种简化分析的方法:串反并同
在学生实际解题过程中,由于这种方法的思维量较大,一道题中要考虑很多个地方,造成了学生对这种方法难以掌握,上手速度慢,尤其是在选择题中,浪费了大量的时间,于是有人就提出了一种简化分析的方法:串反并同。
方法介绍:
在电源的内阻不为零的纯电阻电路中,当电路中某一元件 (用电器或电表) 的电学参量(电阻、电压、电流、电功率)单调增大(减小)时,与之串联的其它元件(用电器或电表)的各个电学参量(电压、电流、电功率)均减小 (增大),也就是所说的“串反”;与之并联的其他元件 (用电器或电表) 的各个电学参量(电压、电流、电功率)均增大(减小),也就是所说的“并同”。
在上述例题中,如果使用“串反并同”的话,可以非常迅速地得出结论:电流表与滑动变阻器串联,其变化规律应该与它的阻值变化规律相反,即触头由a向b滑动时,滑动变阻器的阻值变小,电流表的示数变大。电压表与滑动变阻器并联,其变化规律应该与它的阻值变化规律相同,即触头由a向b滑动时,滑动变阻器的阻值变小,电压表的示数变小。达到了简化问题的效果。
原理分析:
那么为什么可以这么简化呢?
任何的复杂电路,在只有一个局部发生变化时,可以等效为下列两种电路之一:
一种是电源连接滑动变阻器和待分析的用电器串联的电路,另一种是电源连接滑动变阻器和待分析的用电器并联的电路。其中滑动变阻器代表单一变化的局部电路,待分析的用电器代表待分析部分的电路,可以分析流过用电器的电流,加在用电器两端的电压,以及用电器消耗的功率等。
在电路中,利用串并联的规律,先确定待分析用电器,再把发生变化当用电器及其周围的部分等效成为一个新的滑动变阻器,最后将剩余的部分和电源一起等效成为一个新的电源。在确定好滑动变阻器和待分析用电器的串并联关系后,根据“串反并同”规律,可以得出流经待分析用电器的电流、待分析用电器两端的电压、待分析用电器消耗的电功率的变化情况。例如:当确定滑动变阻器和待分析的用电器是串联关系时,当滑动变阻器阻值增大时,整个回路的阻值增大,电源电动势不变,回路电流减小,即流过待分析的用电器的电流减小,加在待分析的用电器两端的电压减小,待分析的用电器消耗的功率减小。这与根据“串反并同”规律分析出来的结果是一致的。
实例应用:
1. 在图1所示的回路中,如果要分析当滑动变阻器阻值增大时,R1的变化情况时,我们可以进行如下等效:将R2以及R3并联的电路等效为一个滑动变阻器,将电压表和电源等效为一个新的电源,滑动变阻器与待分析的用电器R1是串联关系,根据“串反并同”规律有,当滑动变阻器阻值增大时,流过待分析的用电器R1的电流减小,加在待分析的用电器R1两端的电压减小,待分析的用电器R1消耗的功率減小。
2. 在图1所示的回路中,如果要分析当滑动变阻器阻值增大时,R2的变化情况时,我们可以进行如下等效:将电流表和R3等效为一个滑动变阻器,将电压表、R1和电源等效为一个新的电源,滑动变阻器与待分析的用电器R2是并联联关系,根据“串反并同”规律有,当滑动变阻器阻值增大时,流过待分析的用电器R2的电流增大,加在待分析的用电器R2两端的电压增大,待分析的用电器R2消耗的功率增大。
3. 在图1所示的回路中,如果要分析当滑动变阻器阻值增大时,电源内阻r的变化情况时,我们可以进行如下等效:将外电路的所有元件等效为一个滑动变阻器,滑动变阻器与电源内阻r是串联关系,根据“串反并同”规律有,当滑动变阻器阻值增大时,流过电源内阻r的电流减小,加在电源内阻r两端的电压减小,电源内阻r消耗的功率减小。
不适用的情况:
当然了,“串反并同”这个简化性的规律也是基于闭合电路的欧姆定律,在电源内阻不为0,且电路可以简化为原理分析中的那两种情况的闭合回路中才能使用。
1. 如果电源的内阻为0,则“串反并同”的规律不再适用。例如:在图1的情况下,如果电源的内阻为0,那么在分析电压表的变化情况时,不管滑动变阻器怎么变化,都不会影响电压表的示数,都是显示的电源电动势的大小,在这种情况下,“串反并同”规律不再适用。
2. 如果电路不能简化为原理分析中的两种情况时,则“串反并同”的规律不再适用。例如:
当变阻器R的滑动触头P由a端向b端滑动时,求电路中理想电流表的示数变化情况。此时没有办法将电路简化为原理分析中的两种电路,所以无法使用“串反并同”进行分析。应该用函数的方法进行分析:令Rap=R1,对于整个电路有:
当时,I有最小值,故I先减小后增大。
3. 当电路中不是闭合回路时,例如:在一个滑动变阻器和一个电容器串联的回路中,电流表串接在回路中,电压表并联在滑动变阻器两端。当滑动变阻器的阻值增大时,由于有电容的存在,电压表和电流表的读数是不变的,这就与利用“串反并同”的规律进行判断的结果是不同的,此时“串反并同”不再适用。
总之,“串反并同”的结论,在进行电路的动态分析时,能够起到简化问题、提高效率的作用。但是,在享受该结论的便利时,一定要注意其适用条件,在适用的情景下使用,才能起到事半功倍的作用。
参考文献
[1] 杨艳玲.解决电路动态变化的两大方法[J].科技风,2013(14):13.
[2] 林东槟.巧用“串反并同”规律速解电路动态变化及故障排除[J].物理教师,2013(05):89-91.
作者简介:姓名:林志明 出生年月:1991年6月22日 性别:男 民族:汉 籍贯(省市):福建省晋江市 学历:本科 职称:专计十一级 研究方向或从事工作:高中物理
