双流制受电弓结构设计

马 飞，陈 奎，周宇航，李明刚

（中车青岛四方车辆研究所有限公司，山东 青岛266031）

0 引言

受电弓是轨道车辆中重要的部件之一，用于将接触网的电能传导给车内高压设备，为轨道车辆提供动力。双流制受电弓需要满足双流制列车运营要求，适应交流和直流两种供电制式接触网。不同供电制式接触网对弓网接触的参数要求不同，但受电弓都应保持稳定的受流状态，具备良好的受流质量。

双流制受电弓的设计仍然遵循受电弓设计的基本规范，其结构设计内容一般包括运动学设计、机构动力学设计、结构设计和强度校核等，此外还需要进行电气结构设计、弓网动力学分析等方面的工作。受电弓的结构设计是设计工作的基础，由于双流制受电弓实际工作范围大，需要适应两组不同工作参数，为设计工作增加了难度。本文在受电弓结构设计传统方法的基础上，结合动力学分析软件，完成了双流制受电弓结构参数设计，并对设计参数进行了复核和优化，提高了设计工作效率和结构的可靠性。

1 受电弓结构设计

双流制受电弓主要是由底架、下臂杆、推杆、上臂杆、平衡杆、平衡臂以及弓头等几部分组成，形成空间连杆结构，如图1所示。它以安装在底架上的空气弹簧为动力源，驱动下臂杆并带动整个连杆机构实现升弓、降弓动作。同时，在升弓工作状态时，空气弹簧为其提供的恒定接触力。

图1 受电弓结构示意图

受电弓的结构设计应尽可能保证在整个工作高度范围内弓头保持水平状态，即弓头平行度，以防止前后滑板接触不均匀而造成弓头偏磨和离线。另外要求工作高度范围内，弓头在车辆前进方向上的纵向偏移量应尽量小，以符合行业标准要求。在结构动力学方面，要求弓头具有良好的接触性能，即在整个工作高度范围内具有相对恒定的静态接触力。由于不同制式接触网的高度、网压存在差异，双流制受电弓的实际工作范围更大，在不同制式接触网的静态接触力也不相同，因此在设计过程中，需要先选择一种工况进行参数计算，再进行另一种工况的参数校核。

1.1 计算模型

根据双流制受电弓的结构组成和性能要求，按照传统设计方法[1]，选定垂直于主轴和各链轴的对称平面作为研究平面，将结构中各元件向该平面投影，并将各铰链之间简化成杆件，建立受电弓几何关系计算模型，如图2所示。图中，P1-P2代表弓头摆杆，下臂杆DBE为受电弓动作时的主动件。为了便于分析，建模时取推杆AC为主动运动件。

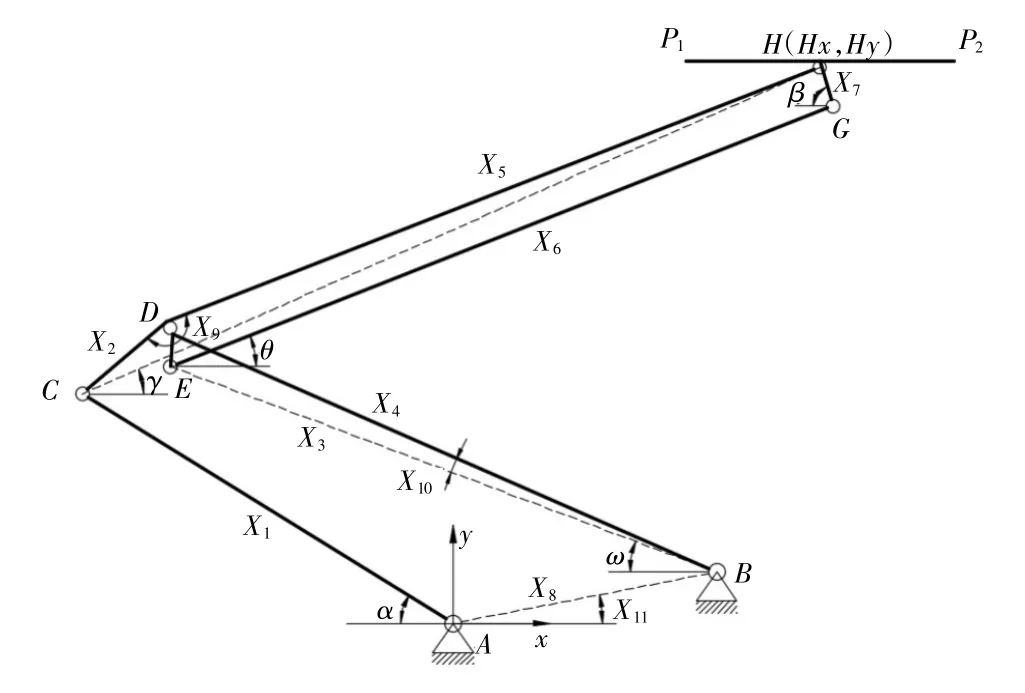
图2 受电弓几何关系计算模型

根据图2，受电弓多连杆机构具有11个需要通过设计计算来确定的变量X1、X2……X11。根据受电弓结构设计要求，通过计算模型的几何关系可以得到：

（1）H点的坐标

式中：lch是C点至H点的距离。

（2）弓头平衡臂GH的偏转角β

其中（Gx，Gy）为G点的位置坐标，其值为：

根据几何关系分析可知，受电弓多连杆机构具有一个自由度，当推杆AC绕固定铰支座A转动时，弓头H点的轨迹（Hx，Hy）及弓头平衡杆GH与水平方向的夹角β就可以唯一确定，即：

式中：Hx（i）为弓头H点轨迹曲线离散点的x坐标分量；Hy（i）为弓头H点轨迹曲线离散点y坐标分量；β（i）为弓头平衡臂在第i个位置与水平方向的夹角；n为离散点数量。

1.2 结构几何参数设计

受电弓结构几何参数设计属约束非线性连续变量最优化设计问题。求解约束非线性问题的方法有多种[2]，此处不再赘述。根据受电弓结构设计要求，应保证在工作高度范围内平衡杆GH应尽量平动，且弓头H点纵向位移尽可能小。根据对多目标问题的求解方法，将多目标问题转化成一个或一系列的单目标问题，即根据设计目标重要程度，选择平衡杆GH平动作为主要设计目标，而将H点的纵向位移转化为约束条件。即机构优化的目标函数为：

各个设计变量应满足：

（1）受电弓正常工作高度范围内，弓头H点轨迹曲线纵向偏移尽量小，即：

其中：Hxmax为离散点x坐标分量的最大值；K为H点允许纵向位移最大值。

（2）为保证正常收弓，受电弓初始位置应能满足：

（3）受电弓的升弓高度应满足要求，即弓头H点的y方向坐标满足：

其中，Hmin和Hmax分别为受电弓最小工作高度和最大工作高度。

上面（1）～（3）中G（i）＜ 0，（i=1，2，…，n+1，n+2，n+3）为n+3个不等式约束条件。

对数学模型进行尺度变换，保证数学模型有更好的收敛性和稳定性。确定各个设计变量的数值范围，并利用建立的受电弓数学模型和优化目标函数及约束条件进行编程计算[3]，就可获得受电弓几何参数设计结果。

2 结构设计校核与分析

以上设计方法解决了受电弓结构设计中的几何参数问题，可以通过动力学分析软件进行受电弓结构动力学建模，对设计参数进行校核和进一步优化。

2.1 结构动力学建模

在初步确定几何参数后，可借助动力学分析软件ADAMS进行受电弓结构动力学建模。按照双流制受电弓的结构和几何关系计算模型，在模型中保留主要部件，整个模型的基准点选取在受电弓前部绝缘子底面中心处，如图3所示。

图3 受电弓结构动力学分析模型

2.2 结构参数的分析和优化

2.2.1 相关性分析

对设计参数进行优化，首先应对优化目标进行参数相关性分析，寻求与之密切相关的变量。将模型设置为参数化模型，利用ADAMS软件相关性分析功能[4]，对弓头平行度、弓头纵向偏移量和接触力变化率等进行参数相关性分析，得到：

（1）弓头平行度与受电弓平衡杆长度X6（E点、G点坐标值）参数密切相关；

（2）弓头纵向偏移量与受电弓上臂杆和推杆的连接位置C点坐标值相关性较高；

2.2.2 弓头平行度

受电弓弓头平行度分析即是对几何关系模型中GH杆的平动验证和优化，利用ADAMS参数化模型和参数优化功能，寻求弓头角度变化率最小时各主要变量参数值。从图4优化后受电弓工作高度与弓头倾角的关系曲线图中可以看出，在工作高度范围740 mm～2 920 mm内，受电弓弓头倾斜角度范围为-1.0°～ 0.4°内。

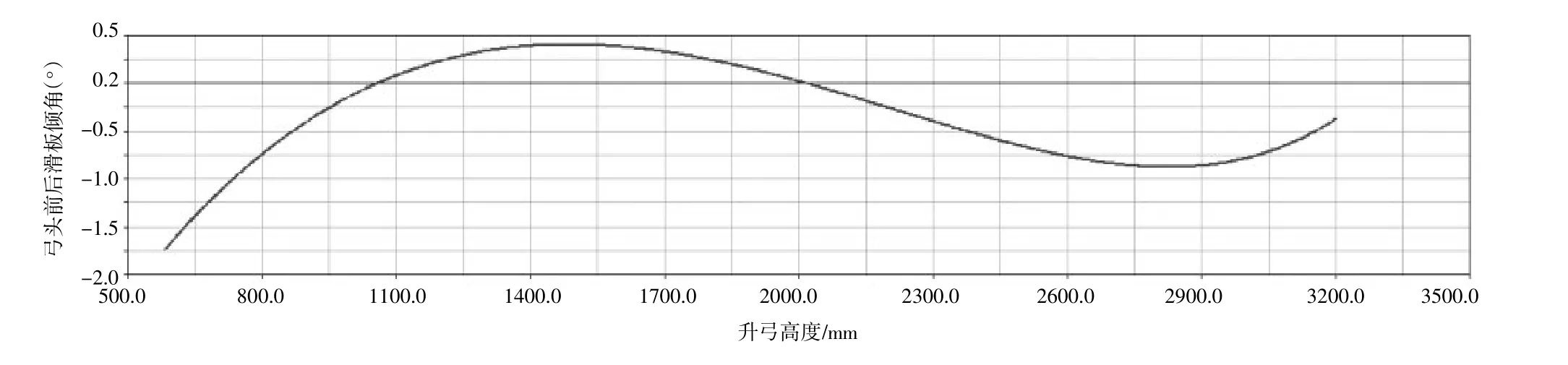
图4 受电弓弓头倾角变化曲线

2.2.3 弓头纵向偏移量

弓头纵向偏移量分析即是对受电弓几何关系模型中H点工作高度范围内的纵向位移量验证和优化。对相关性较高的参数进行优化分析后，得到受电弓弓头H点纵向运动轨迹曲线，如图5所示。在此双流制受电弓工作高度范围740 mm～2 920 mm内，弓头H点的纵向位移约47.5 mm，符合行业标准要求[5]。

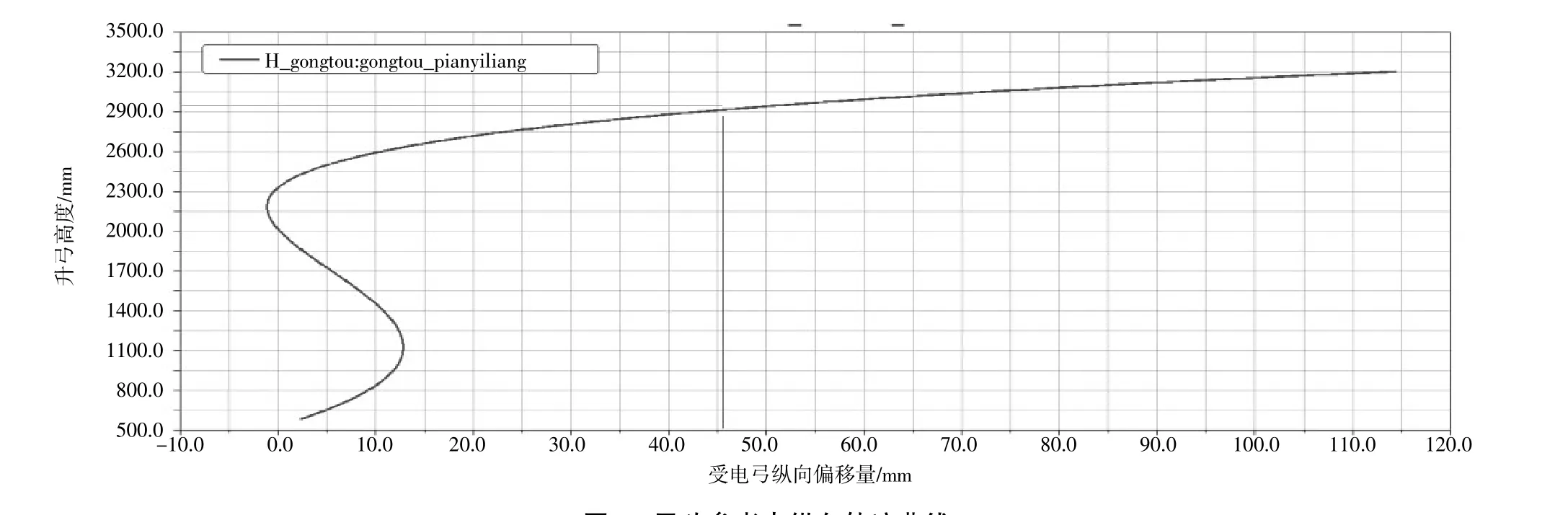
图5 弓头参考点纵向轨迹曲线

3 结构动力学分析

通过上述方法，解决了受电弓结构设计中的几何参数优化问题，还需要解决在受电弓两种工况下工作高度范围内静态接触力保持恒定的技术要求，并求解驱动力参数。

恒定静态接触力是受电弓重要的性能指标之一，通过对动力学分析模型的修改，增加驱动元件，可实现对受电弓接触力的仿真分析。根据仿真分析结果，双流制受电弓对不同制式接触网具备不同静态接触力，其接触力的值是由空气弹簧内充入压缩空气压力决定的，而工作高度范围内静态接触力变化率则是与下臂杆驱动弧形板的外廓曲线密切相关，弧形板的外廓曲线是通过样条曲线拟合而成。

仿真分析得到在不同制式接触网工作时，受电弓静态接触力与工作高度关系曲线如图6所示，图中曲线不平顺是因模型中弧形板与钢丝绳接触设置导致的。根据空气弹簧参数，可以进一步得到空气弹簧工作气源压力。在受电弓工作高度范围内，直流接触网下，静态接触力最小及最大值分别为117 N和122 N，空气弹簧输入压力0.435 MPa；交流接触网下，静态接触力最小及最大值分别为68.5 N和73 N，空气弹簧输入压力0.390 MPa，均符合行业标准要求。

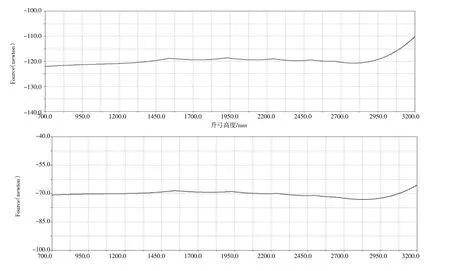
图6 直流接触网和交流接触网受电弓静态接触力仿真曲线

4 试验验证

通过双流制受电弓结构参数优化设计方法，得到受电弓结构几何参数和驱动力参数，根据参数进行结构设计和强度校核等工作，完成了产品设计。利用受电弓性能试验台，按照行业标准进行性能试验测试，并将测试结果与仿真分析结果进行对比。通过数据对比分析可知，双流制受电弓的试验接触力曲线与仿真数据基本一直，数据在行业标准要求范围之内，升弓和降弓过程中的误差是由空气弹簧特性和结构中铰接位置的摩擦力引起的。

图7 受电弓性能试验与测试数据对比

5 结论

利用传统方法进行双流制受电弓结构初步设计，初步确定受电弓结构的几何参数。在此基础上，利用动力学分析软件建立结构动力学参数化建模，对受电弓弓头平行度、弓头纵向偏移量、静态接触力等重要指标进行参数相关性分析，寻求各个指标的强相关参数。对弓头平行度、弓头纵向偏移量等指标进行校核并进一步完成参数优化，对弓头静态接触力进行仿真分析，完成对驱动力参数的计算。通过传统设计方法和动力学模型分析相结合，简化了设计方法，提高了设计效率和设计参数可靠性。产品的性能试验结果表明，受电弓静态接触力符合相关标准要求并与理论分析基本一致，证实了设计方法的有效性。