基于Variance-Brenner函数的显微图像清晰度评价算法研究
2021-01-13王灿芳崔良玉
王灿芳 ,崔良玉 ,阎 兵
(1.天津职业技术师范大学,天津300222;2.天津市高速切削与精密加工重点实验室,天津300222)
0 引言
传统的显微镜进行图像观察需要人工手动调焦,这种聚焦方式速度慢,对于批量化显微观察,容易让人疲劳,而且由于人的主观因素存在错误判断的可能。自动聚焦是提交检测效率、减轻劳动量的有效技术,而图像清晰度评价函数是自动聚焦技术中判断图像是否清晰的重要依据[1]。自动聚焦方法主要分为被动式聚焦和主动式聚焦[2],主动式聚焦通过计算物体与像面的距离根据成像原理得出与焦点的位置差,从而驱动镜头完成自动对焦。而被动式聚焦是基于数字图像处理,通过对采集的一系列图像进行数据分析来判断当前图像的聚焦程度。被动式聚焦不需要其他的传感设备,仅使用捕捉的一系列图像就可以完成聚焦,因此应用广泛[3]。图像越清晰,表明其含有更多的细节和边沿信息,在频域上表现为图像包含更多高频成分,因此可以根据这些理论研究评价图像清晰度的算法。传统的数字图像清晰度评价算法主要是基于空域、频域、统计学和信息熵等[4-5]。基于梯度的算法根据图像的梯度信息来判断图像的清晰程度,这类方法计算简单,应用广泛,但抗噪性较差;频域类则使用傅里叶变换、小波变换、离散余弦变换等,计算图像中的高频分量来评价图像是否清晰,这类算法比较复杂,计算量大;统计学类的算法,虽然计算量小,但灵敏度较低[6]。本文对各类传统的算法进行了仿真分析,针对基于空域类算法和统计学类算法的优点及不足,提出了一种将方差函数与Brenner函数相结合的算法。
1 传统的图像清晰度评价函数分析
基于数字图像的聚焦办法有离焦深度法(DFD)和聚焦深度法(DFF)。DFD法依靠获取两幅及以上距离焦点不同位置的图像,运用数学的方法并结合成像,计算出物体与焦点的距离,从而推断出正确的焦点。由于这种调焦方法是通过建立成像系统的数学模型来计算离焦量,而数学模型只能近似估计,因此存在较大误差。DFF法是通过对每一帧数字图像进行处理,根据图像包含信息的丰富程度来评价图像是否聚焦,这种方法精确度高,因此应用广泛。基于DFF方法的图像清晰度评价算法主要分为基于梯度、频域、统计学和信息熵四类,梯度类函数计算简单、稳定性好,应用最为广泛。
1.1 基于图像梯度的清晰度评价函数
根据焦点位置的图像与远焦图像相比具有更多的边缘信息且灰度值变化明显这一原理[7-9]来评价图像的清晰度。典型的梯度函数[10-11]主要有方差函数(Variance)、Tenengrad函数、Roberts函数、Laplace函数、能量梯度函数(EOG)、灰度差分绝对值之和函数(SMD)、Brenner函数等[12]。
(1)方差函数(Variance)
方差(Variance)函数表征图像灰度信息的离散水平。处在焦点位置的图像灰度变化明显,离散水平高,方差大,而其他位置灰度变化小,方差也相对较小[13-14]。因此可以用灰度变化的平均程度来评判图像是否正确聚焦。M*N大小的图像清晰度评价值如公式(1)所示:

式中,F是图像的清晰度评价值;M和N是图像的高度和宽度(以像素为单位);f(x,y)表示对应像素点的灰度值。μ为图像的平均灰度,定义如式(1-2)所示:

(2)Tenengrad 函数
运用Sobel算子提取像素点垂直、水平方向的梯度值,取像素点梯度的平方和,并设定梯度阈值T控制算法灵敏度。定义如式(3)所示:

其中,G(x,y)是像素点(x,y)处的梯度。如式(4)所示。

Gx(x,y)和Gy(x,y)代表像素点(x,y)水平方向和竖直方向的梯度值。其定义式如式(5)所示:

其中,⊗为卷积运算符,gx、gy分别代表Sobel算子水平方向和竖直方向的模板:

(3)Roberts函数
Roberts函数取像素点(x,y)处4个相邻像素点的灰度值,进行交叉相减并取平方和,再将所有的和相加,以此值来评价图像清晰度。定义式如(6)所示:

4)Laplace函数
将图像各像素点的灰度值与Laplace算子进行卷积运算,得到梯度矩阵G(x,y),取G(x,y)的平方和作为评价函数,如式(7)所示:

Laplace算子:

(5)能量梯度函数(EOG)
将数字图像水平和与垂直方向相邻的像素点的灰度值做差,再进行平方运算,然后将逐个平方运算的和作为评价函数值。定义如式(8)所示:
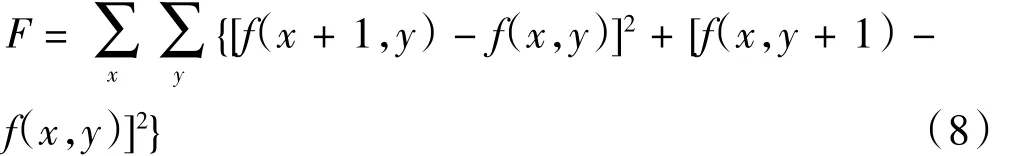
(6)灰度差分绝对值之和函数(SMD)
SMD函数分别将x方向和y方向相邻像素点灰度值差分的绝对值之和累加作为图像清晰度评价函数的值,避免了复杂的乘方运算。其定义式如(9)所示:
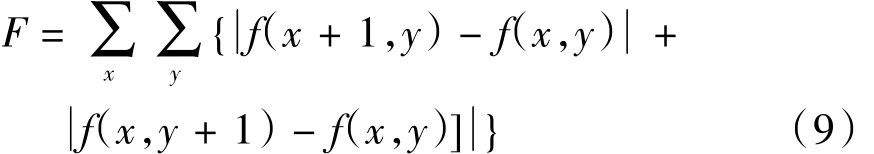
(7)Brenner函数
Brenner函数将相邻两个像素点灰度之差的平方累加,优点是计算量小,灵敏度高,但对噪声比较敏感。定义式如(10)所示:

1.2 其他图像清晰度评价函数
越清晰的图像含有的高频成分越多,据此可以使用傅立叶变换把图像梯度信息变换成频域进行分析,判断图像的清晰度。典型的频域类算法有基于二维离散傅里叶变换的评价函数(2D-DFT)和离散余弦变换评价函数(DCT)。但频域类算法需要对图像进行频域变换,算法复杂,计算量大。根据香农信息论,熵可以用来描述信息的丰富程度。熵越大图像中包含的信息量也就越多,对应的图像越清晰,但基于信息熵理论的算法稳定性较差,且计算复杂。由于算法依据的原理不同,复杂性不同,使得函数各有优缺点。而实际的评价函数曲线由于受到噪声和光照不均等因素的干扰,容易造成局部极值的出现而致使聚焦失败。因此,有必要设计一种既能满足实时性,又满足计算简单、精度高、稳定性好的算法。
2 仿真与分析
使用显微镜系统的CCD摄像机采集了23幅由远焦到正焦点的图像,为了提高计算速度,将图像尺寸改为128*128像素大小,并进行灰度化处理。部分采集图像及灰度化结果如图1所示。并使用MATLAB软件对梯度类的图像清晰度评价算法进行仿真,结果如图2所示。

图1 部分采集图像及灰度图

图2 梯度类图像清晰度评价函数仿真图
从图2中可以看出,显微图像在自然条件见下极易受到噪声的影响,从而导致图像清晰度评价函数出现较大的波动。因此对图像进行高斯滤波处理,使用sigma=0.8的3*3高斯模板进行平滑处理,高斯滤波对图像中的高斯白噪声有很好的的消除作用。经过高斯滤波后的各类算法仿真结果如图3(a)所示,可以看出图像经过高斯滤波后各类评价函数曲线的性能都有了明显的改善。然而图像中的噪声是随机的,比如椒盐噪声,中值滤波是非常理想的消除椒盐噪声等随机噪声的滤波器,因此在对图像进行高斯滤波后继续进行中值滤波处理,函数仿真结果如图 3(b)所示。

图3 中值滤波的函数仿真图
从图 3(b)与图 3(a)的仿真结果对比来看,对图像进行高斯滤波和中值滤波后,可以有效的地去除图像中的噪声,使得各算法的仿真曲线变得更光滑,消除了局部极值,峰值区域更陡峭,提高了算法的灵敏度和稳定性,性能提升明显。其中,Laplace函数曲线改善最为显著。
3 融合Variance函数与Brenner函数的清晰度评价算法
理想的图像清晰度评价函数应该是一条光滑的曲线,在峰值区域附近陡峭,在远焦区域平坦,应当具有单峰性、无偏性、鲁棒性、灵敏度高和计算简单的特点。因此本文选择基于空域的梯度类算法作为图像清晰度评价函数。
从图3(b)中可以看出,Brenner函数灵敏度高,函数曲线在峰值区域最为尖锐,而Tenengrad函数和方差函数稳定性好,不易受噪声的干扰。基于鲁棒性考虑,要求评价函数尽可能的光滑,防止聚焦搜索时陷入局部极值,远焦区域曲线平缓,无太大波动。基于灵敏度考虑,函数曲线的峰值附近区域要陡峭。从实时性考虑,函数应该计算简单。结合以上分析,Brenner函数灵敏度高,方差函数在远离峰值区域曲线平缓,且两种函数计算简单,因此,综合两种函数的优点提出一种新的图像清晰度评价函数VB。如式(11)所示:

其中,μ同公式(1-2),FVB表示图像清晰度评价函数值。
在对图像进行滤波处理的基础上,将本文提出的融合Variance函数与Brenner函数的Variance-Brenner(VB)算法与Variance函数、Brenner函数及Tenengrad函数进行仿真比较,结果如图4所示。
可以看出,本文 Variance-Brenner算法(VB)在峰值区域更尖锐,斜率更陡峭,在远离峰值区域的平缓区域相较于其他函数也更平缓。显然,本文图像清晰度评价算法要优于方差函数、Brenner函数和Tenengrad函数。
4 结束语
本文对不同类型的图像清晰度评价算法进行了研究,并用MATLAB软件进行了仿真分析。考虑到显微图像容易受噪声的干扰,将图像进行了滤波处理,仿真结果表明通过去燥处理后,各类函数性能均有明显改善。通过仿真结果分析了各算法的优缺点,其中Brenner函数灵敏度高,但稳定性稍差,而方差函数稳定性高,且两种函数计算简单,计算速度快。根据互补的原则,本文提出了融合Variance函数与Brenner函数的Variance-Brenner(VB)算法。仿真结果表明本文提出的算法明显优于方差函数、Brenner函数和Tenengrad函数。
