滑坡预测预报中改进的Pearl模型及其应用

贺小黑

(1.北京城建勘测设计研究院有限责任公司，北京 100101；2.城市轨道交通深基坑岩土工程北京市重点实验室，北京 100101；3.东华理工大学核资源与环境国家重点实验室，江西 南昌 330013；4.东华理工大学水资源与环境工程学院，江西 南昌 330013)

0 引言

Pearl滑坡预测预报模型是孙景恒[1]基于生物学研究领域的Pearl方法提出了Pearl生长曲线模型。Pearl曲线的特征表现为下部比较平缓，曲线斜率较小，生长速度较慢;中部斜率最大，即生长速度最快;生长曲线的上部，生长接近上限，生长速度极慢以至于达到成熟，此时生长终止。这与斜坡的发展演化过程极为相似。

滑坡的变形发展过程经历了缓慢变形、均匀变形、加速变形及失稳破坏4个发展阶段，类似于Pearl生物生长曲线的发展过程。在边坡缓慢变形和均匀变形阶段，边坡的变形较小，主要是蠕变， 相当于生物生长的发生阶段；边坡加速变形阶段，曲线斜率比较大，相当于生长的发展阶段；边坡破坏阶段，变形急剧加速，然后趋于稳定，这个阶段相当于生长成熟阶段[1-2]。

目前，Pearl模型主要应用于预测农药浓度[3-4]、沉降[5]等方面，用Pearl模型进行滑坡预报研究的学者较少，只有孙景恒、缪海波等学者进行相关研究。孙景恒等分析认为可采用选点法或者变换法求得Pearl曲线方程式中的a、b、k三个未知参数，将求出的参数代入到Pearl曲线方程式中即可得到相应的Pearl滑坡预测预报模型。他提出可把Pearl曲线中上部分分界点(拐点)作为所寻找的预报点，他采用了长江新滩滑坡和意大利Vaiont滑坡资料对Pearl生长曲线预报模型进行了分析与验证。结果表明，Pearl生长曲线预报模型对于边坡失稳时间预报是适用的，所得结果与实际发生时间基本吻合，可适用于边坡失稳破坏的中、短期预报[1-2]。由于用Pearl模型进行滑坡时间预报的研究很少，故还无法将Pearl模型的预报结果与其他模型的预报结果进行对比。少量学者用Pearl模型开展了滑坡变形预测方面的研究，并与其他模型的预测结果进行对比，如缪海波等以三峡库区八字门滑坡为例，分别用非平稳时间序列模型、Pearl生物生长模型及BP 神经网络模型对滑坡变形趋势进行预测，结果表明Pearl模型的预测效果最好，BP 神经网络模型次之，这说明八字门滑坡变形趋势较符合Pearl 生物生长模型所描述的类型[6]。陈小亮认为Pearl模型的后期演变曲线同滑坡实际位移加速变形阶段曲线的形态存在较大的差异，故其剧滑时间预测预报的物理基础存在一定的问题[7]。

孙景恒提出可采用选点法或者变换法求得Pearl曲线方程式中的a、b、k三个未知参数。对于选点法而言，需要选取时间相距等值的3个合适的数据点，如果数据点选择不当，则所得到的预测预报结果不可靠。由于选取计算的数据点时没有一定的标准，且三个数据点不一定能把所有数据点的变形趋势反应出来，故选点法确定的Pearl生长曲线不一定能较好地表现位移监测数据的变形趋势；变换法在求取参数时虽然综合所有数据点的信息来确定a、b、k，但是该方法并不是按照预测误差最小的原则去确定参数。因此，选点法和变换法在求参数上都有缺陷，需要提出更加合理、预测误差最小的方法来确定Pearl生长曲线方程中的参数。

此外，孙景恒等提出可把Pearl曲线中上部分分界点(拐点)作为所寻找的预报点[1-2]，但是他并没有给出计算该滑坡预报拐点所对应时间的计算公式，本文根据Pearl曲线方程推导了速度最大值和加速度最大值判据的预报公式，并根据几个实例的预报结果对比了这两个判据的预报效果。该研究对于Pearl模型应用到滑坡预测预报中具有重要意义。

1 Pearl模型在滑坡预测预报中的应用原理

Pearl生长曲线是根据有机体的生长所得到的描述生物生长的数学模型，其数学模型一般形式为：

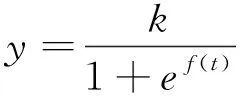
(1)

式中：k——常数；

f(t)——自变量t的多项式。

即：

f(t)=a0+a1t+…+amtm

(2)

最常用的生长曲线f(t)属于一次多项式，且其一次多项式系数为负值的情况。

即：

f(t)=a0+a1t

(3)

将此多项式代入式(1)得：

(4)

式中：a、b、k——系数，a=-a1，b=ea0;

y——t时刻的位移监测值。

一般情况下，所给边坡变形监测数据(ti,yi)，按时间顺序排列为：

(t1,y1),(t2,y2),…,(tn,yn)

其中：t——时间。

若能应用Pearl曲线来拟合这些数据，只需求出式中的a、b、k三个参数即可进行滑坡时间预报。

孙景恒提出可采用选点法或者变换法求得Pearl曲线方程式中的a、b、k三个未知参数。

选点法是在给定的(ti,yi)数据中，选择t相距等值的3对变量，用以同时估算出a、b、k三个数值的方法。对所选用变量的3个数据点，必须能够代表曲线首段、中段、末段的位置，且3个ti值成等差级数。如果不能从给出诸数据(ti,yi)中选取适当的3个点时，必须选用经过平均处理的变量的3对数据。求平均值时，在生长曲线的首段、中段、末段各取3对或4对数值，分别进行平均，y值的平均方法可采用几何平均法。

设选择的3对原始数据或经过平均处理的变量值为(0，Y0)，(m，Ym)，(2m，Y2m)，且拟合的生长曲线通过此3点。则由(4)得：

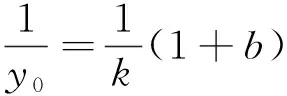
(5)

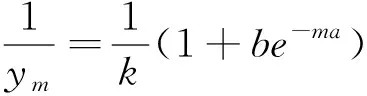
(6)

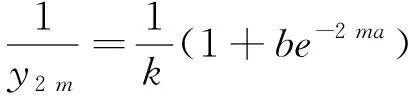
(7)

令：

(8)

(9)

则：

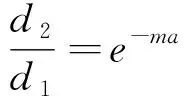
(10)

由此可得t的计算公式为：

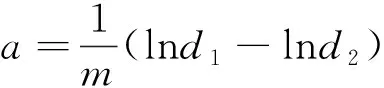
(11)

由(5)式可以得出：

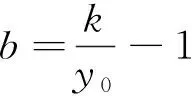
(12)

d1，d2的表达式相减即得：

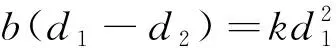
(13)

解以上联立方程可得：

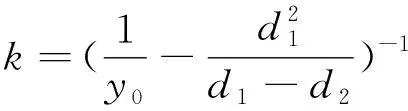
(14)

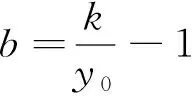
(15)

将以上所得到的a、b、k代入曲线方程，即得到拟合的生长曲线方程[1-2]。

2 滑坡预报中对Pearl模型的改进

2.1 对参数求取方法的改进

求取Pearl曲线方程式中的a、b、k三个未知参数的方法有选点法或者变换法。

对于选点法而言，需要选取时间相距等值的3个合适的数据点，如果数据点选择不当，则所得到的预测预报结果不可靠。由于选取计算的数据点时没有一定的标准，且三个数据点不一定能把所有数据点的变形趋势反应出来，故选点法确定的Pearl生长曲线不一定能较好地表现位移监测数据的变形趋势；变换法在求取参数时虽然综合所有数据点的信息来确定a、b、k，但是该方法并不是按照预测误差最小的原则去确定参数。因此，选点法和变换法在求参数上都有缺陷，需要提出更加合理，预测误差最小的方法来确定Pearl生长曲线方程中的参数。

本文运用1stOpt软件中的麦夸特法(Levenberg-Marquardt)和通用全局优化法，对实测数据进行非线性拟合，进而确定参数a、b、k。较选点法和变换法而言，由于本文选用的非线性拟合确定参数的方法采用了最小误差原则的拟合方法，所得到的曲线能较准确地表现出原始位移监测数据的变化趋势，故本文的方法优于选点法和变换法。

2.2 对Pearl模型滑坡预报判据的公式推导

孙景恒等提出可把Pearl曲线中上部分分界点(拐点)作为所寻找的预报点[1-2]，但是他们并没有给出计算该滑坡预报拐点所对应时间的计算公式，本文参考文献[8]对判据的研究论证，推导了Pearl模型速度最大值和加速度最大值判据的滑坡时间预报公式。

对(4)式进行一次、二次、三次求导得：

(16)

(17)

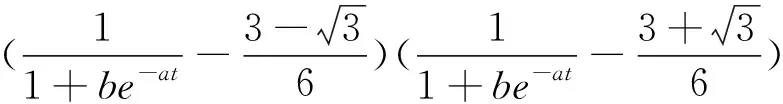
(18)

当位移速度达到最大值时，y′(t)取得极大值，此时y″(t)=0。令(17)式右端等于0，解方程得：

(19)

求解(19)式得：

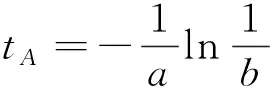
(20)

tA为基于速度最大值判据的滑坡发生时间预报值，式(20)为该判据滑坡发生时间预报值的计算公式。

当位移加速度达到最大值时，y″(t)取得极大值，此时y‴(t)=0。令(18)式右端等于0，解方程得：

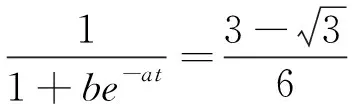
(21)

求解(21)式得：

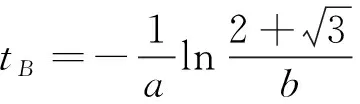
(22)

tB为加速度最大值判据的滑坡发生时间预报值，式(22)为该判据滑坡发生时间预报值的计算公式。

2.3 滑坡预报改进的Pearl模型的实例应用

基于滑坡预测改进的Pearl预报模型，依据文献[9]提供的卧龙寺新滑坡位移监测资料进行预报。卧龙寺新滑坡实际发生时间是1971年5月5日。原始位移数据见表1。表1中位移数据单位为mm。

为了分析改进模型是否能较早地进行预报，本文舍弃了表1中最后两个数据，选取了1971年3月15日至1971年5月3日的位移数据进行分析，首先对预报原始位移监测数据进行了平滑处理，原始位移-时间曲线和经平滑处理后的曲线见图1。

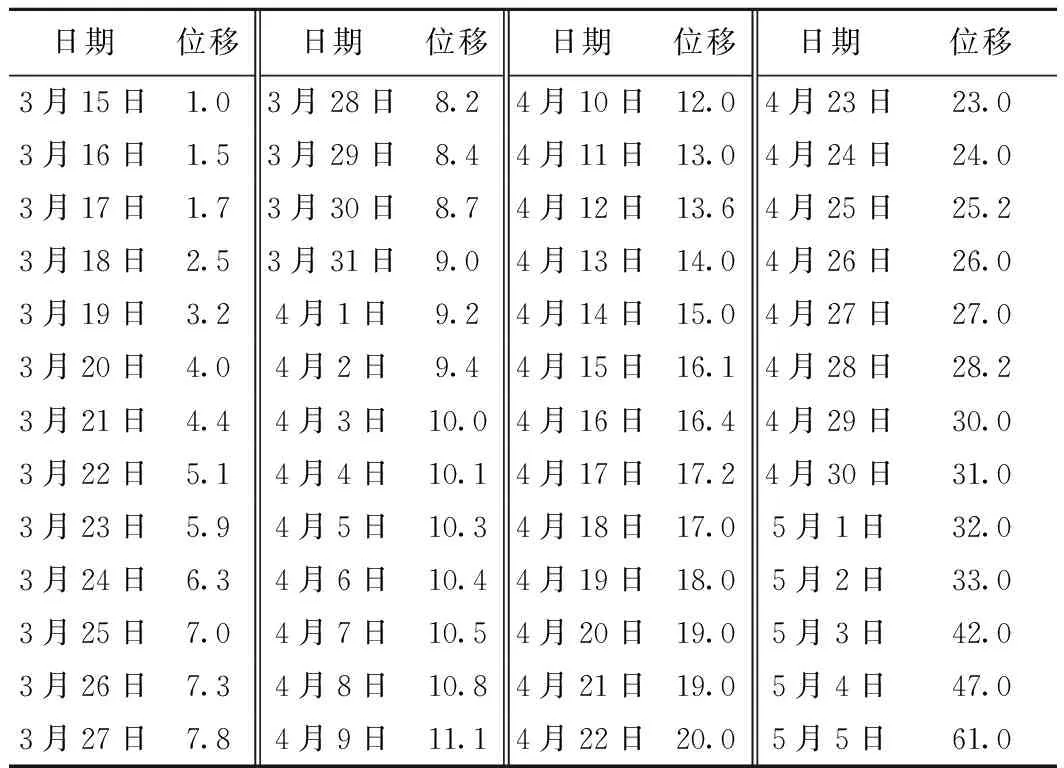
表1 卧龙寺新滑坡位移监测值Table 1 Displacements of Wolongsi new landslide /mm

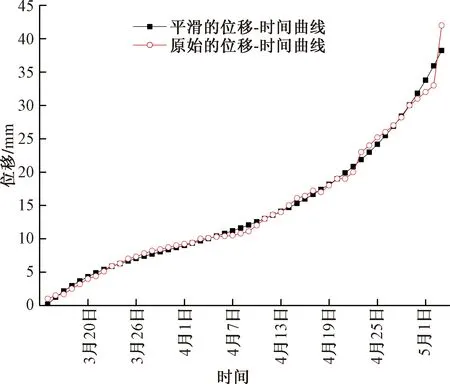
图1 卧龙寺新滑坡原始和平滑后的位移-时间曲线Fig.1 Original and fitted displacement-time curve of monitoring point of Wolongsi’s new landslide

由平滑结果可知，从1971年3月30日至1971年5月3日，位移速度不断增大，由于Pearl模型适用于加速变形阶段，故选取1971年3月30至1971年5月3日的经平滑处理后的加速数据进行预报。

通过非线性拟合确定Pearl模型中的参数a和b，把模型速度和加速度最大值判据应用到卧龙寺新滑坡时间预报中。预报结果如表2所示。

表2 卧龙寺新滑坡剧滑时间预报结果Table 2 Forecast results of Wolongsi’s new landslide

由预报结果可知，滑坡实际发生时间介于Pearl模型速度判据和加速度判据的预报时间之间，用Pearl模型加速度判据能起到提前预报的作用，且加速度判据较速度判据更合理，故用Pearl模型预报时建议用加速度判据预报。

3 结论

(1)针对原始Pearl模型求取模型未知参数的方法存在较大缺陷的问题，将非线性拟合的方法应用到模型未知参数的求取中，所得到的Pearl滑坡位移预测曲线能较准确地表现出原始位移监测数据的变化趋势。

(2)基于位移量的Pearl模型方程基础上推导了以速度和加速度极大值时刻作为预报滑坡发生时间判据的计算公式。将改进的模型参数计算方法和两种不同判据应用到滑坡实例的预报中，结果表明：滑坡实际发生时间介于Pearl模型速度极大值判据和加速度极大值判据的预报时间之间，用Pearl模型加速度极大值判据能起到提前预测预报的作用。