工业机器人空间圆弧算法的实现

南京埃斯顿自动化股份有限公司 江苏 南京 211106

0 引言

机器人的轨迹规划,在机器人控制中具有重要的作用,直接影响着控制的准确性和快速性。而插补算法是整个机器人轨迹规划控制过程的精华所在,占据着举足轻重的地位。通过示教机器人运动路径上的某些关键点,然后根据轨迹特征算出这些示教点之间必须到达的中间位置点,通过插补进行控制,从而实现高效率高精度的运动控制。

当曲线轨迹为圆弧时,除了示教圆弧起点和终点外,至少还应知道圆心或圆弧上一个辅助点。显然,示教圆心是很困难的,因而工业机器人终端执行器的轨迹圆弧通常由示教的圆弧起点、辅助点及圆弧终点决定,而这三点所决定的平面通常不一定平行于某一坐标平面,因而需要研究空间任意三点圆弧的插补算法[1]～[4]。

目前普遍采用基于坐标转换的空间圆弧插补方法,即通过坐标转换将空间圆弧转化为平面圆弧[5],利用平面圆弧插补算法进行计算,之后再通过坐标转换把插补点从平面结果转换为空间结果。此方法需要进行多次坐标变换,计算过程复杂,计算工作量大。现有空间圆弧插补方法未提及过辅助点姿态;随着工业发展的进步,控制指令的简便,某些特殊应用场合如焊接、涂胶等需要经过辅助点的姿态。

针对以上问题,提出了一种用于工业机器人的过辅助点姿态空间圆弧插补方法。该插补方法示教任意不共线的空间三点,不需要坐标转换将空间点转换成平面点进行计算,而是直接进行空间离散点的计算,并且对姿态进行规划使其过辅助点姿态,能根据给定的圆弧起点、辅助点及终点完成任意空间圆弧插补。

图1 空间圆弧插补算法的流程图

2 空间圆弧插补算法

本算法的基本技术方案为:机器人控制器通过通信端口确定了示教器示教的空间不共线三点;根据空间几何关系直接进行空间离散点的计算,求出空间圆弧的圆心、半径、法向量、圆心角和弧长;对姿态进行规划使运动轨迹经过辅助点姿态且轨迹光滑;速度轨迹规划模块计算出每个插补周期的插补位移;利用实时插补算法计算出每个插补周期的插补点位姿;将最终满足示教要求的位姿通过通信端口提供给机器人运动机构并执行。

2.1 空间圆弧的圆心、半径、法向量、圆心角和弧长的求解 机器人轨迹上各点位姿由位置矢量(x,y,z)和RPY姿态矢量(α,β,γ)共同描述,组合成一个6自由度的复合矢量(x,y,z,α,β,γ),即(x,y,z,a,b,c)。通过外部示教器示教确定工业机器人的要求位姿,机器人控制器通过通信端口获取示教器提供的示教点信息;确定工业机器人轨迹的空间圆弧起点、辅助点及终点空间坐标及位姿,分别为:P1(x1,y1,z1,a1,b1,c1)、P2(x2,y2,z2,a2,b2,c2)、P3(x3,y3,z3,a3,b3,c3);

空间圆弧的圆心、半径、法向量、圆心角和弧长的求解的步骤具体如下:

第1步,在空间坐标系中,空间圆弧起点、辅助点及终点为不共线的空间三点,确定了空间圆弧所在的平面(简称圆弧平面),根据圆心到三点的距离都为半径的条件,联立方程,计算可求出圆弧的圆心P0(x0,y0,z0),进而求得由三点确定的圆弧的半径R;

第2步,根据外积公式,可求得垂直于空间圆弧平面的单位法向量n⇀(nx,ny,nz);

第3步,根据余弦定理和三个角之间的关系,求得空间圆弧的起点到辅助点、辅助点到终点、起点到终点的圆心角分别为:θ1,θ2,θ3(θ3=θ1+θ2)(如图2);

第4步,根据圆弧弧长公式,求得弧长L=Rθ3;进而求得空间圆弧插补的总位移S;

图2

2.2 姿态规划模块规划出经过空间圆弧辅助点的姿态 机器人各轴姿态随圆心角变化的变化率公式为:

分别对w(θ)积分即是机器人各轴姿态值,故可根据极值法设计使得各轴姿态变化率连续,并求得相应的系数值k1,m1,k2,m2;

2.3 轨迹速度规划模块,计算出每个插补周期的插补位移 轨迹速度规划模块,可以规划基于梯形曲线加减速控制或基于S形曲线加减速控制或其它曲线控制;根据不同的曲线控制方式,进行速度规划处理,计算圆弧段所需要的插补总时间和插补信息,最后计算出每个插补周期的插补位移;

2.4 计算得到插补点的空间位姿 根据空间圆弧平面的法向量和插补位移,计算机器人空间圆弧插补点位姿Pi(xi,yi,zi,ai,bi,ci)步骤如下:

第1步、根据圆弧弧长公式,每个插补周期的插补位移除以半径得到空间圆弧每个插补周期的插补角度θ;

第2步、利用以下公式可求得插补点的空间坐标位置

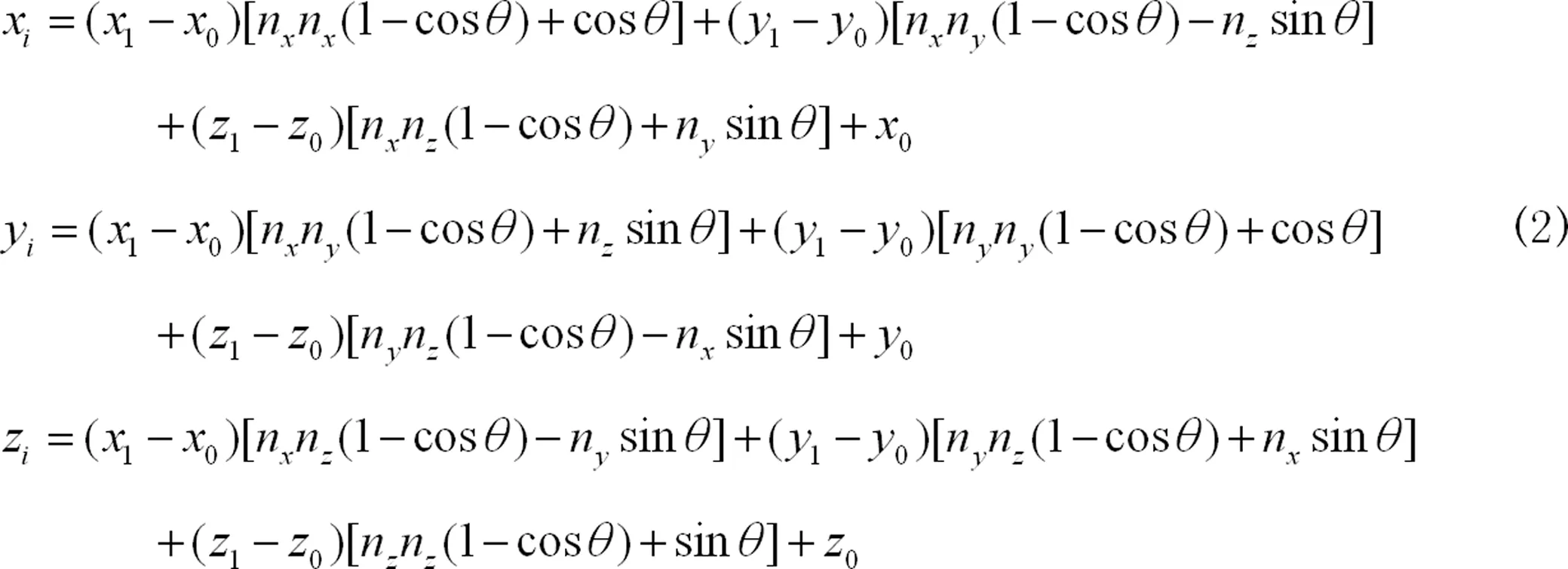
第3步、利用以下公式可求得插补点的姿态

最后,机器人控制器的中央处理器将最终得到的位姿通过通信端口提供给机器人运动机构进行执行。本文实现的方法可以实现工业机器人的高精高效的运动控制,经过辅助点姿态,并且运动平滑。

3 结束语

本文实现的方法根据空间任意三点进行圆弧插补,避免了示教圆心的困难和确定圆弧方向的问题。不需要进行坐标转换计算平面圆弧插补,而是直接计算空间角度和空间离散点得到实际空间圆弧插补点坐标,方法过程简洁方便、算法易于实现、计算效率高、插补精度高。过姿态规划模块,使得实际空间圆弧插补点经过辅助点姿态,满足某些特殊应用场合。实现姿态变化率与插补角度的连续关系,使得各轴姿态变化连续,机器人运动平滑。