东北女青年下身体型分类及数学模型建立

张小妞， 王 军*,2， 张春媛

(1. 大连工业大学 服装学院，辽宁 大连 116034;2. 大连工业大学 服装设计与工程国家级实验教学示范中心，辽宁 大连 116034)

人体的体型复杂，而下装纸样结构设计的方法较多，若要达到下装合体性与舒适性要求，人体下身体型分类及数学回归模型的建立是重要基础。近年来，已经有文献对不同地区、不同年龄的人群进行人体数据分析，研究人体下身体型特征、分类及识别的方法[1-2]，其中对女性下身体型特征研究开展最早的是华东地区。

目前国内外对体型的分类主要采用数据分析的方法，使用SPSS软件从不同角度对体型进行聚类，根据研究目的选择分类指标，包括特殊指标、主成分等。当针对特殊体型或特殊部位时，采用特殊指标进行分类，如张秀等[3]以身高、裆底高、身高与裆底高的比值作为分类指标，将女性下身分为4类；夏岩等[4]以臀凸角为聚类指标，将臀型分为4类；黄灿艺[5]以下身长宽比和腰臀比为聚类指标，将下身分为4类；张雨[6]以腹凸倾斜角为腰臀部初次分类的指标，再运用K-means聚类法，将武汉地区女性腰臀部细分为6类；CHOI Y L等[7]运用体侧角将人体侧身形态分成4类。围度差可以反映人体体型的变化，是下身分类最常用的指标。黄英等[8]、葛秋菊[9]均以腰臀差作为体型分类标准，将华东地区女性下身体型分为4 类；陈明艳等[10]以臀腰的围度差、宽度差、厚度差为依据，将女性下身分为5类。此外，王军等[11]运用主成分分析法，得到5大主成分变量指标，将女性下身分为3类；程朋朋等[12]测量福州大学学生的体型数据，并进行主成分分析，提取7个特征因子用于分析样本体型，研究结果将女子体型分为3类，男子体型分为4类；SONG H K等[13]运用主成分分析法，将女性臀部分为3类，将女性腰臀部分为9类。

1 人体测量实验

1.1 仪器

VITUS三维人体扫描仪，德国Human Solution 公司制造。

1.2 实验变量的确定

文中研究对象为677名大连工业大学青年女性，年龄为18～25岁。文中主要参考人体体型特征、人体运动特点、裤装结构3部分，对人体下身进行研究。女性下身主要分为腰臀部和腿部两个部分，裆部是连接两者的重要部位。根据人体及服装结构规律选定人体测量项目，测量项目应尽可能反映下身体型特征，以有效描述人体腰、腹、臀的曲面特点。结合女性下装结构要求，除测量女性下身的周裆长、直裆长、腰围、臀围、腰高等基础部位外，还需要测量腰、腹、臀的宽度和厚度，同时大腿根部、膝部、脚踝也是下身研究的重点部位。实验选取24项人体下身数据分析东北女青年下身体型特征，具体测量变量见表1。

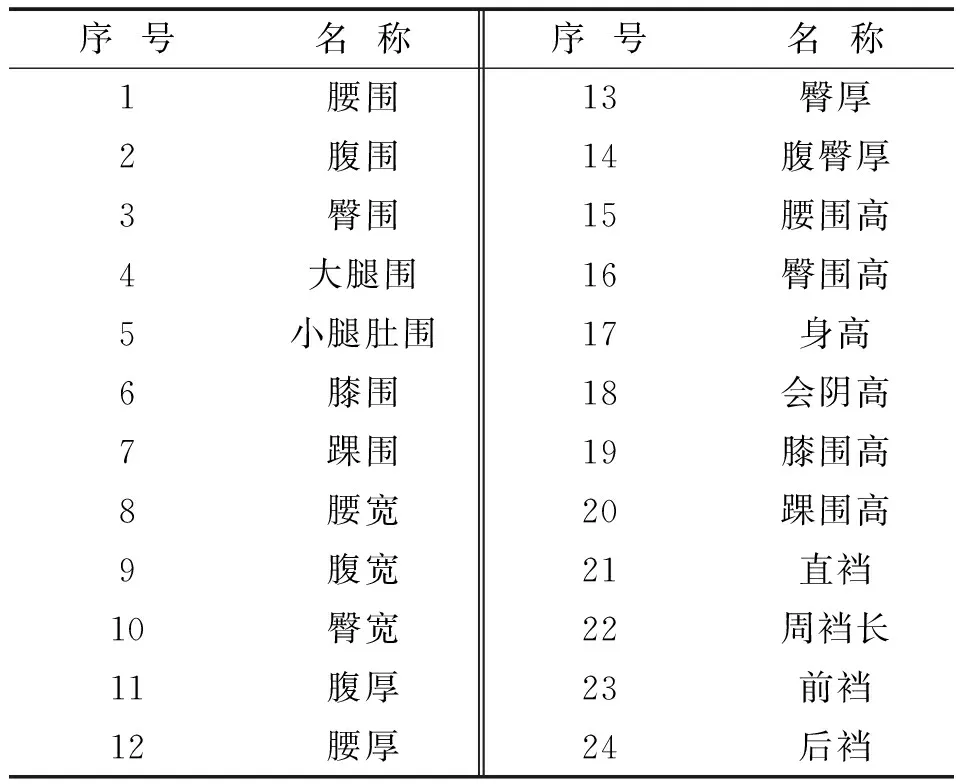
表1 下身体型变量

1.3 样本量的确定

一般在工业生产和科学研究中，为保证测量数据的准确性，取95%置信水平，最小样本容量为[14]

(1)

式中：N为最小样本容量；σ为标准差；Δ为最大允许误差；α为5%，对应的可靠性系数zα/2为1.96。

表2为成年人体部位尺寸的最大允许误差和标准差[15]。由表2可知，最小样本容量为173，而实际测量对象人数为677，满足样本要求。

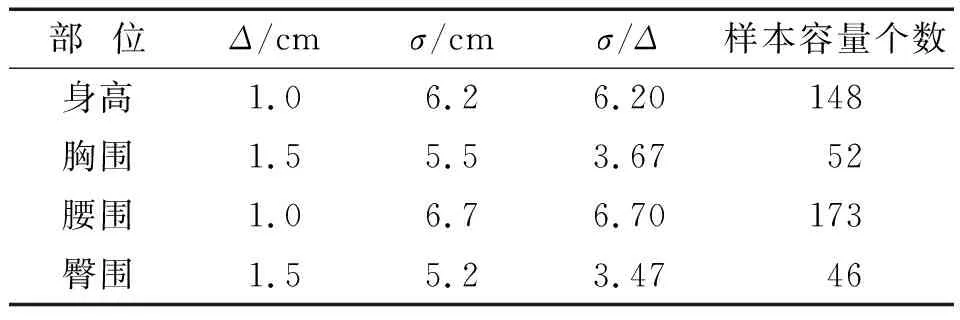
表2 成年人体部位尺寸的允许误差和标准差

2 数据处理

2.1 正态分布检验

进行人体数据分析时，要求样本服从正态分布。文中采用Q-Q概率图对东北女青年下身体型数据进行正态检验，以臀围为例，检验结果如图1所示。由图1可以看出，臀围变量与正态期望值形成的点大致落在一条斜线上，因此可认为臀围数据服从正态分布。经验证其他指标也服从或近似服从正态分布。

2.2 异常值分析

由于测量过程中存在偶然误差和系统误差，通过SPSS软件的箱式图排查东北女青年下身体型数据中的异常值。以臀围为例，所得箱式图如图2所示。图2中，各异常值可以直观呈现。

对于数据异常的样本，需要查看、分析原始三维扫描的数据，综合判断数据的有效性，剔除异常值。通过对数据的预处理，综合分析后排除50个异常的东北女青年下身体型数据，最终确定627个有效样本，样本有效率为92.6%。

2.3 下身体型特征分析

2.3.1下身体型变量统计分析 对东北地区青年女性下身腰臀部及腿部变量进行统计，得到各测量项目的极小值、极大值、均值、标准差，结果见表3。表3显示了东北地区女青年下身数据的离散程度和变异范围，总体上反映了东北地区女性下身体型情况。

2.3.2下身体型特征比较 将18～25岁东北地区女青年(样本1)与国标女子标准体(样本2)的下身体型数据平均值进行比较，结果见表4。由表4可知，东北地区女青年在围度上与标准体有明显差异，腰围比标准体小，身高略高，整体较标准体更为高挑。

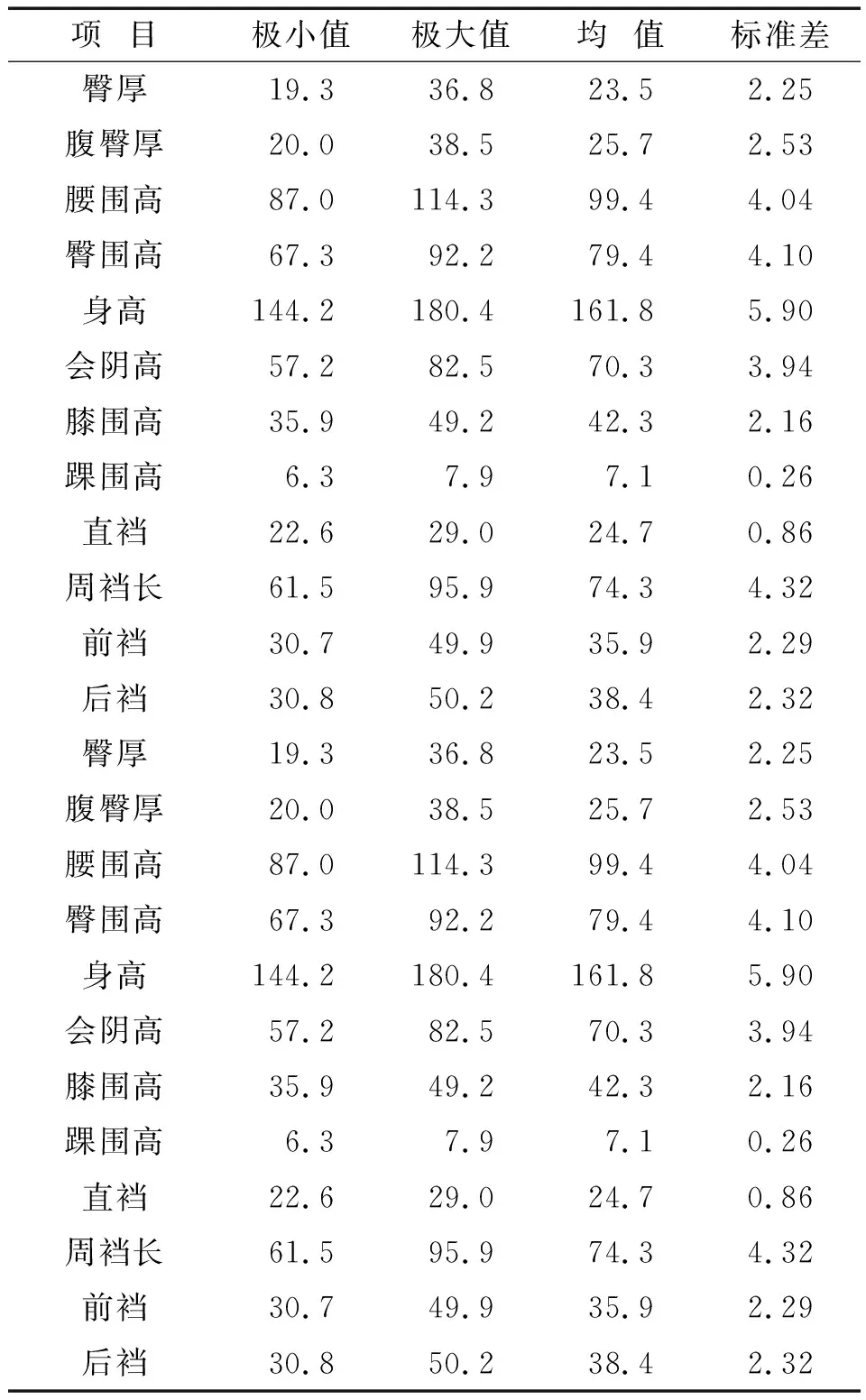
表3 东北地区青年女性下身指标统计

表4 样本下身均值与国标下身均值对比

2.4 主成分因子分析

对东北女青年下身体型特征的24项指标进行KMO值的适当性度量和Bartlett's球形检验，结果见表5。由表5可以看出，测量实验中女青年下身体型指标KMO值为0.897，Bartlett's球形检验值为0.000，说明这24项体型特征指标适合进行因子分析。

表5 KMO和Bartlett's检验

为探索影响东北地区女青年下身体型的主要因子，运用SPSS软件对实验样本进行主成分分析，结果见表6。由表6可以看出，前3个主成分累计方差贡献率为86.545%，特征值大于1，因此影响东北地区女青年下身体型的主要因子有3个。

表6 方差总解释

旋转后的成分矩阵见表7。由表7可以看出，主成分因子1在围度、宽度、厚度变量上有较大载荷，可定义为横向因子；主成分因子2在高度上载荷系数较大，可以定义为高度因子；主成分因子3在裆部变量上有较大载荷，定义为裆部因子。

表7 旋转后的成分矩阵

综上，影响东北地区女青年下身体型特征的3大因子为：横向因子、高度因子和裆部因子。

2.5 下身体型聚类

采用K-means聚类法对东北地区女青年下身体型进行分类。K-means聚类法用于对大量数据进行聚类分析的情形，可以有效处理多变量、小计算量、大样本的数据而不占用太多内存空间和计算时间，其速度往往明显快于层次聚类法，但对变量的多元正态性、方差齐性等条件要求较高[16]。通过对测量数据的分析，从3大因子中筛选出具有代表性的下身体型特征参数，提取身高、周裆长、腰围3个变量，运用K-means聚类法对实验样本进行聚类分析，发现东北地区女青年下身体型可分为3类，各类体型样本占比分别为16.1%，35.3%，48.6%，样本聚类分布情况见表8。聚类后各体型类别的特征变量平均值见表9。

表8 聚类分类情况

表9 最终聚类中心

数据标准化处理可以消除变量间的量纲关系和变量自身变异的影响，统一数据单位，使数据具有可比性。SPSS默认的数据标准化方法是Z-score法，这种方法基于原始数据的均值和标准差进行标准化，即每一变量值与其平均值之差除以该变量的标准差[17]。运用SPSS标准化方法对各类体型的分类变量进行标准化处理，结果见表10。

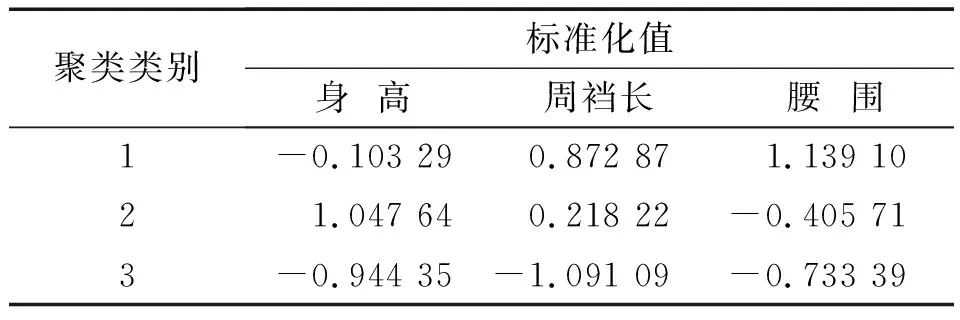
表10 各类体型特征变量标准化

根据表10各类体型特征变量标准化结果绘制雷达图，用于分析东北地区女青年下身体型聚类类别的差异，具体如图3所示。由图3可以看出，聚类1腰围和周裆长最大，身高比较适中，其下身体型特征为中等身高胖体；聚类2身高最高，腰围和周裆长适中，其体型特征为高挑标准型体；聚类3身高、腰围和周裆长均小，其下身体型特征为瘦小体。

利用方差分析法验证K-means聚类中将下身体型分为3类是否合理，结果见表11。表11中，Sig.值均为0.000，可以看出所有变量在组间与组内均有明显差异，验证聚类数为3具有合理性。

表11 方差分析

2.6 数学回归模型

根据各项特征指标的Pearson相关性分析，以身高h与腰围w作为自变量，对腰围高、会阴高、臀围等12项与裤装相关的特征指标进行逐步回归分析，建立各类体型的数学模型，以研究人体下身变量与身高、腰围之间的函数关系，具体结果见表12。

表12 各类体型数学回归模型

由表12可以看出，在围度指标中，第1类体型的数学回归模型均为二元一次函数，说明围度受身高和腰围的影响；第2和第3类体型中，大腿围、膝围和踝围的h系数比较小或者为0，说明主要受腰围的影响。在高度指标中，3类体型的w系数较小或为0，说明主要受身高的影响，腰围影响较小或不受影响。在臀厚指标中，3类体型的数学回归模型均为一元一次函数，说明臀厚主要受腰围的影响。在周裆长指标中，第1类和第3类体型的数学回归模型均为二元一次方程，说明裆部指标受身高与腰围的共同影响。

3 结 语

1) 通过对下身体型特征指标描述统计的对比与分析，发现在下身体型特征方面，东北地区女青年与国标女子标准体有明显差异，整体呈现围度偏小、身高偏高的特点。

2) 运用SPSS进行主成分因子分析，得到3个影响下身体型特征的主成分因子，分别为横向因子、高度因子和裆部因子。依据3大因子选取腰围、身高、周裆长3个变量为分类指标，运用K-means聚类法对下身体型进行分类，将东北女青年下身体型分为中等身高胖体、高挑标准体、瘦小体3类，各类体型占实验样本的比例分别为 16.1%，35.3%，48.6%；3种体型的腰部特征差异较明显。

3) 根据各项特征指标的Pearson相关性分析，选择身高与腰围为自变量，对12项与裤装相关的特征指标进行逐步回归分析，得到各类体型的数学回归模型。