液体火箭发动机试验脉动压力数据分析方法研究

杨 懿 蹇 玥 贾志杰 王永鹏 郭亚男

(北京航天试验技术研究所，北京 100074)

1 引 言

在液体火箭发动机试验中，压力是反映发动机和试车台设备工作过程特性的重要参数[1]。根据所测压力信号随时间的变化类型，压力参数可分为稳态压力和脉动压力。稳态压力一般用于考察和研究发动机、试验台工艺系统的能力。脉动压力一般用于测量燃烧室、推力室内高频、高压、高温压力，能弥补稳态压力测量方法在高、低温和水击压力等特殊环境下测量能力的不足。

针对脉动压力数据的特点，研究行之有效的数据分析方法，挖掘测量数据背后的有价值信息是研究发动机动态性能和燃烧状态的重要手段。

脉动压力参数数据采样率高，系统响应频率快，仅仅分析数据在时域内的信息是远远不够的，还需要深度挖掘数据的其他信息。商霖[2]等通过研究燃烧室内脉动压力能量分布的频率特性与随机振动的关系，研究发动机的工作原理。刘英元[3]等以数据频率为研究对象，通过FFT方法和小波变换方法提取发动机状态特征的方法。费继友[4]等将小波分析与奇异值检测理论相结合，应用小波奇异检测和误差滤波对瞬态数据进行处理，通过试车试验验证该方法有效。

本文采用FFT方法和小波变换奇异点检测方法对发动机脉动压力数据进行分析，提取特征信息，研究发动机的不稳定燃烧状态。

2 脉动压力测量系统组成和数据特征

2.1 系统组成

脉动压力测量系统一般由脉动压力传感器、传感器循环冷却系统、供电电源、信号转换装置、数据采集和分析系统组成，系统组成图如图1所示。

图1 脉动压力测量系统组成图Fig.1 Fluctuating pressure measurement system diagram

2.2 数据特征

脉动压力数据需要精确体现燃烧室、推力室等高温、高压、剧烈振动环境下的压力变化信息。测量系统一般具备以下特征：测量系统的频率响应快，通常在10kHz以上；传感器耐高温、高压和剧烈振动，频率特性至少应有10k～20kHz的平坦段；采集系统采样率高，一般具备10kHz/s以上的高采样速率。因此，脉动压力数据具有高频、采样点多和数据容量大的显著特征。

3 脉动压力数据分析方法

本文采用两种方法分析某型号发动机地面试车的脉动压力数据：(1)FFT分析方法。结合相应振动测点的数据，分析脉动压力数据的幅频特性，为判断是否发生不稳定燃烧提供依据。(2)采用小波分析法对数据进行去噪、奇异点检测，研究发动机动态性能和燃烧状态。

4 数据分析方法的理论基础

4.1 FFT理论基础

在数字信号分析领域，FFT是分析非周期信号频域信息的重要工具。该方法利用傅里叶积分能够将非周期的函数在无限区间上分解的性质，对连续时域信号进行抽样和截断，实现数字信号计算机分析处理。

窗函数的选择是FFT的重要步骤，直接影响频谱分析的结果。常见的窗函数有Hamming窗、Hanning窗、矩形窗和Bartlett窗。Hanning窗具有主瓣宽、旁瓣峰值低、衰减速度快和能有效减少频谱泄漏的优点，本文采用Hanning窗进行数据分析。

4.2 小波分析的理论基础

小波分析法通过小波基函数的伸缩和平移实现信号时频两域自适应分析，凭借其强大的挖掘信号细节信息的能力，近年来在工程应用领域得到了广泛的应用[5]。

信号的奇异性分析是提取信号特征信息的重要手段。在工程应用中，信号的奇异点包含系统运行过程中很多的重要信息，对奇异点的分析能够挖掘系统运行的关键信息。

采用小波分析法将突变奇异信号进行多尺度分解，根据Lipschitz指数和模极大值在不同尺度上的关系分析信号的突变特征并定位奇异值的位置和大小。通过对信号奇异点突变时间、突变类型和变化的幅值等参数的考查，对发动机的燃烧状态进行分析[3]。

4.2.1小波变换与分解重构

设φ(t)为一个基本小波，L2(R)表示平方可积的实数空间，φ(t)∈L2(R)，若其傅里叶变换函数Ψ(ω)满足条件

(1)

式中：R——实域；ω——属于实域R的变量。

设伸缩系数为a,a>0且连续可变化数值。设平移系数为b，b∈R且连续可变化数值。将基本小波函数φ(t)进行伸缩和平移，令伸缩和平移后的函数φa,b(t)为

(2)

式中：φa,b(t)——依赖于a,b变化的连续小波基函数。

对于将脉动压力数据视为非周期信号，用函数x(t)来表示，其连续小波变换的表达式为

WTx(a,b)=〈x(t),φa,b(t)〉=

(3)

式中：WTx(a,b)——表示对函数x(t)进行以a,b为系数的连续小波变换。

调整a和b的大小，不仅可以将信号分解到各个指定的频带，还可以保留各分量的时域信息。为了便于计算机进行计算分析，需要将连续小波函数、a和b离散化[5]。离散化的方法通常把伸缩系数a和平移系数b取幂级数。在实际的应用中，对a和b进行二进离散时一般取a0=2,b0=1，即a=2j，b=k2j，j,k为整数。

小波变换方法对信号进行分析处理时一般采用Mallat算法将信号进行多重分解与重构。算法的基本原理是：利用小波高通、低通滤波器对函数x(t)在分辨率2j下进行分解，获取低频和高频小波系数。小波重构则是小波分解的逆运算。采用相关算法将高、低频小波系数进行重构[6]。

4.2.2小波突变点检测的基本原理

在小波分析方法中，通常用Lipschitz指数α描述信号的奇异性。随着小波变换尺度的增加，小波变换的模极大值在信号奇异点的衰减速度取决于信号在突变点的指数α。

采用小波变换来描述连续信号f(t)在t0点的奇异指数。设小波基具有n(n为正整数)阶消失矩，且n阶可微、具备紧支撑特征。令f(t)∈L2(R)。若在t0点的邻域和所有尺度上，存在常数K满足

|WTf(s,t)|≤K(sα+|t-t0|α)

(4)

式中：|WTf(s,t)|——对函数f(s,t)进行以s、t为系数的连续小波变换；K——常数；s、t——大于0的常数；t0——数据中的奇异点；α——f(t)在点t0处的Lipschitz指数为α,0<α≤n。

从公式(4)可以看出，信号奇异点分布在模极值线上，其Lipschitz指数α不等于1，突变信号呈现奇异性且指数α>0。当t0为信号f(t)的局部奇异点，t取离散值，则在该点的小波变换取得模极大值。在离散二进小波变换中，公式(4)变换为

(5)

式中：j——二进尺度参数；A——常数。

从公式(5)可以看出，如果信号在t0处的奇异指数大于零，则随着尺度j的增加，小波变换模极大值也增加。在应用中，通过小波变换后的模极大值在不同分解尺度上的衰减速度衡量信号的局部奇异性。当小波函数可以看作平滑函数的一阶、二阶导数时，信号小波变换模的局部极值点和过零点分别对应于信号的突变点[7]。因此可建立信号奇异点与模局部极大值之间的关系。但是模极大值与奇异点之间并非一一对应的关系，只有在多个尺度上检测均为极值点的位置才是真正的突变点所在位置，继而进一步确定突变点的类型。在进行奇异点定位之前，需要对数据进行去噪处理，排除系统中噪声的干扰[4]。

小波奇异点定位分析的步骤为：对信号进行小波离散化处理；对信号进行小波分解；对利用小波函数对信号进行去噪；对信号进行奇异点定位、分析；对分解信号进行小波重构。

4.2.3小波基函数的选择

在工程应用中，常用的小波基函数有：Haar函数、DbN函数、SymN函数、CoifN函数和Dmey函数等几种。各种基函数都有自身的特点，使用的基函数不同，得到的处理结果也不一样。在实际的运用过程中需要根据数据和小波基函数自身的特点，选择合适的小波基函数进行数据处理[3]。

小波基函数的选取主要遵循三点原则：(1)支撑长度是指尺度函数、小波函数及其傅里叶变换的收敛速度；紧支撑基函数的收敛速度快，在描述原始信号时能减少计算量，提高计算的精度。而非紧支撑基函数的收敛速度慢，在描述原始信号时的计算效果和逼近效果要差一些。(2)在选择基函数时，一般应选择具备紧支撑特征的基函数。(3)对称性能够有效避免信号处理中的移相问题，正则性和消失矩呈正相关关系，主要影响小波系数重构的稳定性。各种小波基函数的特点如表1所示。

表1 各小波基函数特点Tab.1 Characteristicsofwaveletbasisfunctions名称Haar函数DbN函数SymN函数CoifN函数Dmey函数特点正交、紧支撑、单个矩形波、矩形状阶梯变化、计算简单正则性好、对称性好、频域的局部化能力强、频带划分效果好、紧支撑、消失矩光滑性好DbN函数的一种改进型、具备DbN函数的优点、对称性比Db函数好对称性比Db函数好不具备紧支撑性、收敛速度快

5 发动机试验脉动压力数据分析

5.1 FFT分析

采用FFT方法分析试验数据时，一般需要针对发动机不同的工况，如启动段、稳定段和关机段等工况分段分析。以某次发动机试验稳定段工况的燃烧室脉动压力数据为例。选取稳定段0.2s(2000个样本点)的数据进行FFT频谱分析，数据采样率为10kHz/s，测点参数名为Pfs。试验全程脉动压力数据如图2所示，稳定段0.2s数据如图3所示。为了能够清晰观察数据样本在各频率段内的幅值变化情况，分别列出(0～5000)Hz和(0～11000)Hz频率段的频谱分析图，如图4、图5所示。

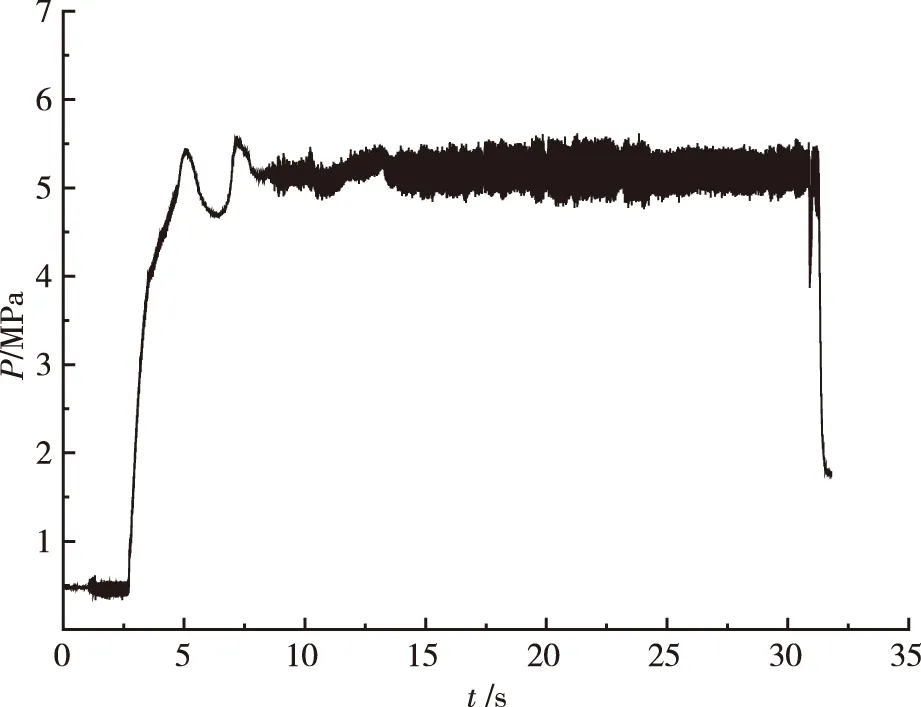
图2 Pfs全程脉动压力数据图Fig.2 Pfs pressure conduit system diagram

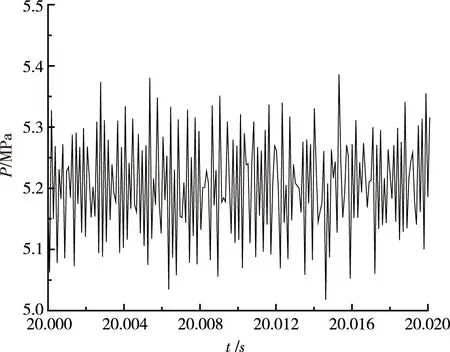
图3 Pfs测点0.2s脉动压力数据图Fig.3 0.2s fluctuating pressure data of Pfs measuring point

图4 脉动压力Pfs(0～11000)Hz频谱分析图Fig.4 Spectrum analysis diagram of fluctuating pressure Pfs(0～11000)Hz

图5 脉动压力Pfs(0～5000)Hz频谱分析图Fig.5 Spectrum analysis diagram of fluctuating pressure Pfs(0～5000)Hz

图3中稳定段0.2s脉动数据可以看出，燃烧室内脉动压力幅值大致在(5.0～5.4)MPa范围内波动且呈现周期性的压强振荡特征。从图4和图5的FFT数据分析频谱图可以看出幅值峰值主要集中在(0～5000)Hz的频率段内，(0～1000)Hz的中、低频率段的幅值波动不明显，(1000～5000)Hz高频段出现多个幅值峰值，且振幅的幅值呈递增趋势。说明随着推进剂燃烧对压强振荡响应，燃烧产生的能量持续注入燃烧室工作系统。由此可以推断发生高频声振的可能性较大。

为研究稳定段的不稳定燃烧声振的类型，采用FFT分析方法对燃烧室轴、径、切向三个振动测点数据进行分析。径向振动测点ab1-2的频谱分析结果如图6所示。可以看出在(1000～5000)Hz频率段，径向振动测点ab1-2存在多个幅值峰值。

图6 ab1-2振动测点频谱分析图Fig.6 Spectrum analysis diagram of ab1-2 vibration measuring point

轴、径、切向三个振动测点FFT频谱分析幅值峰值频率点和脉动压力数据幅值峰值频率点的对比分析情况如表2所示。

表2 燃烧室振动测点与脉动压力幅频数据表Tab.2 Vibrationmeasurementpointsandamplitudefrequ-encydatatableofpulsatingpressureincombustionchamberPfs幅值峰值对应的频率(Hz)ab1-1(轴向)ab1-2(径向)ab1-3(切向)904╱╱╱1611╱√╱2243╱╱╱2884╱√╱3685╱╱╱4822√√╱9643╱√╱ 注:√表示在振动数据FFT分析的幅值峰值的频率值与Pfs吻合;╱表示在振动数据FFT分析的幅值峰值的频率值与Pfs不吻合。

通过表2的分析数据可以看出，脉动压力测点Pfs的幅频峰值特性与振动径向测点ab1-2的幅频峰值特性在1611Hz、2884Hz、4822Hz和9643Hz四个频率点，即发动机工作频率的2、6、12倍频存在耦合关系，而与轴向和切向的耦合点较少，由此可以推断燃烧室发生高频横向声振。通过上述分析得出结论：脉动压力数据可以清晰地反映燃烧室内的压强振荡；燃烧室内产生不稳定燃烧时，通过对脉动压力数据进行FFT分析可以获取其幅频特性。通过分析脉动压力和振动测点的频谱特征，可以为判断发动机燃烧不稳定性声振的类型提供强有力的参考依据。

5.2 小波奇异点分析

某次发动机试验燃烧室脉动压力测点Pios1全程试验数据如图7所示。从图7可以看出在发动机试车启动段和关机段的脉动压力波动异常。

图7 Pios1脉动压力全程数据图Fig.7 Pios1 fluctuating pressure data chart

分别选取启动段(3.18～3.58)s，样本点数4000和关机段(12.29～12.39)s，样本点数1000的数据进行奇异点特征分析。数据采集系统采样率均为10kHz/s。

5.2.1启动段数据分析

启动段(3.18～3.58)s的数据如图8所示。在奇异点检测中，选择小波的正则性非常重要。根据对各类小波的特征分析，分别采用db1和db9小波对启动段的数据进行相似系数计算、FFT分析和7层分解重构。由于篇幅关系，仅列出数据处理效果较好的db9小波分析结果。db9小波分解7层近似系数结果如图9所示。(0～10000)Hz和(0～250)Hz的FFT分析局部放大效果图分别如图10、11所示。采用db9小波7层分解细节系数结果如图12所示。

图8 Pios1启动段脉动压力局部数据图Fig.8 Local data diagram of pulsating pressure in Pios1startup section

图9 小波分析相似系数图Fig.9 Similar coefficient graph of wavelet analysis

图10 FFT幅频特征图(0～10000)HzFig.10 FFT amplitude frequency characteristic chart(0～10000)Hz

图11 FFT幅频特征图(0～250)HzFig.11 FFT amplitude frequency characteristic chart(0～250)Hz

图12 db9小波7层分解细节系数图Fig.12 db9 wavelet 7-level decomposition detail coefficient diagram

从图8中可以看出，启动段脉动压力存在多个峰值波动，且平均压强呈递增的趋势。从图9中可以看出，7层分解重构后的相似系数图在波峰个数以及波峰对应数据点与图8的原始数据基本一致，表明采用db9小波对数据进行处理很好吻合了数据的变化趋势。从图10和图11的FFT分析结果可以看出，FFT方法能够分析数据在频域的特征，由于没有时间分辨力，无法提取压力幅值突变点的空间位置和特征信息。图12列出了采用db9小波对数据进行7层分解后的细节系数。图中可以看出，d1～d7的7层分解信号中均准确定位了原始信号中幅值突变奇异点的位置。7层分解信号中的噪声随着分解尺度的增加迅速减少，第6、7层分解重构后的曲线存在一定程度的失真，主要因为分解层数越高，过滤掉了更多有用的信息。第4、5层分解重构的效果最好，能够清晰地观察到信号中的不连续点和幅值突变点。d1～d3的高频细节系数显示信号中高频部分是原始信号中突变的主要成分。通过对该时间段燃烧室轴向、径向和切向振动测点的进行FFT频谱分析，发现a3切向振动测点在高频段(2000～8000)Hz能量较集中，高频段振幅远高于低频段振幅。此外，a3切向振动测点高频段的振幅均大于同频率段轴向和径向的振幅，且a3测点在工作倍频之外还出现了多个振动峰值。燃烧室a3切向振动测点频谱图如图13所示。

图13 燃烧室关机段a3切向振动测点频谱分析图Fig.13 Spectrum analysis of a3 tangential vibration measuring point in shutdown section of combustion chamber

通过上述分析可以判断在发动机试车的启动段，燃烧室存在不稳定燃烧，在燃烧室切向产生高频声振，导致在启动段脉动压力的高频段存在多个峰值奇异点。

5.2.2关机段数据分析

关机段原始数据如图14所示。采用模极大值法，选取db9小波对原始信号进行7层分解重构，分解尺度为1～32。小波变换系数如图15所示。

图14 Pios1关机段脉动压力局部数据图Fig.14 Local data diagram of pulsating pressure in Pios1

图15 小波变换系数与分解层数结果图Fig.15 Results of wavelet transform coefficients and decomposition levels

从图15可以清楚看出，在第50、876、918、984样本点，小波系数呈现一个倒锥形的区域，且在2、4、8、16、32层分解的尺度上，小波变换系数均呈现一致间断的特征(均为白色区域)。由此可以判断在第50、876、918、984样本点，信号均为奇异信号。该结论与图14中原始数据的波动非常一致。从图14的原始数据中可以观察到在上述奇异点，脉动压力的幅值存在(7.88～10.49)MPa幅度的异常波动。

6 结束语

根据脉动压力数据的特点，本文给出了基于FFT和小波变换奇异点检测的液体火箭发动机试车脉动压力数据分析方法。通过对脉动压力数据和相应振动测点的FFT频谱分析，能够在频域内有效判断发动机燃烧室的工作状态和声振类型。但是由于傅里叶变换在时域内的局限性，无法对信号中的突变点进行定位。采用基于小波变换模极大值和Lipschitz指数的小波奇异点检测方法对发动机启动段和关机段的异常数据在多个尺度进行分解分析，不仅能有效定位信号中的突变点位置，还能获取信号在频域内的信息。结合相应振动测点的频谱数据分析结果，能够为判断发动机燃烧状态和声振类型提供有力的依据。上述两种方法在其他型号发动机和组合件试验的脉动压力数据分析中也具有重要的推广价值。