多套光学经纬仪联合跟踪的容错最小距离平方和定位
2021-01-12梁家辉胡绍林
梁家辉,李 建,胡绍林,3*
(1. 西安理工大学 自动化与信息工程学院,陕西 西安710048;2. 中国兵器工业试验测试研究院,陕西 华阴714200;3. 广东石油化工学院 自动化学院,广东 茂名525000)
1 引 言
经纬仪是一种根据测角原理设计的测量俯仰角和方位角的测量仪器,通常有光学经纬仪和电子经纬仪两种类型。1730 年光学经纬仪最早由英国机械师Sisson 研制,1904 年德国开始生产玻璃度盘经纬仪。随着电子技术的发展,20 世纪60 年代出现了电子经纬仪。光学经纬仪的水平度盘和坚直度盘均用光学玻璃制成,电子经纬仪采用编码度盘、光栅度盘、电栅度盘或记时测角度盘,实现了数字化自动测角。
无论是光学经纬仪还是电子经纬仪,都是用于测定远处目标位置,广泛应用于大地测量、地图绘制、雷达标校、飞机校飞、导航制导、火箭跟踪及卫星轨道测定等领域[1]。
经纬仪定位的基本原理是利用两台(或多台)经纬仪分别测定目标相对于经纬仪轴心位置的俯仰角E 和方位角A,利用多组测角数据(A,E),采用几何交会算法或最小二乘法,逐点计算目标点在参照系下的坐标,实现目标位置解算。经典的交会算法主要有K-公式法、L-公式法或最小二乘法[1-4],以及最小一乘等改进方法。K-公式和L-公式虽有简洁的解析表达式,但是只用到部分数据信息,精度受限;最小二乘或最小一乘法,虽用到全部测量数据,但涉及非线性方程求解,不便于数据快速计算,且对野值数据缺乏容错能力;基于L-公式提出的4 台经纬仪两两交会测量结果的加权融合处理方法[5],虽然精度较高,但不适用于三站或多站的交会测量;文献[6]和[7]对该方法进行了改进,可适用于两站和三站交会测量,但随目标飞行高度的增加,基于L-公式的融合处理方法的误差不断增大,性能会迅速下降;HOU 等人提出了基于两个相交平面公垂线的异面直线法[8],SU 等人对K-公式、L-公式法和异面直线法精度做了比较,证实3 种方法在不同适用区的定位精度差异较大[9]。
本文提出一组基于最短距离和的多台站经纬仪测角数据融合容错定位方法。该方法直观、简单,对野值数据具有容错能力,通过求解线性方程组即可得到目标轨迹坐标,能实现对于全部测角数据的融合,不受野值数据的影响。
2 基于最短距离和的融合定位

图1 经纬仪测量数据的几何关系示意图Fig. 1 Geometric relationship of theodolite measurement data
假设测定目标M 在任意t 时刻的空间位置,记经纬仪在t 时刻的测量数据为( t,A,E )。由于单台经纬仪的任一组数据都不可能单独确定出M的位置,即使测量数据是理想值,也只能确定t时刻飞行器在射线Li上某个位置,如图1 所示。
如果有N台经纬仪同时跟踪该目标,可假设目标M在t时刻应该同时在图2 所示的N条射线上,即M应该在这N条射线的交点上。但是,实际中测量数据中不可避免地含有误差,误差的存在使得这N条射线未必相交于一点。这N条射线最多可以相交于C2N个不同点,当然也有可能没有交点,这就使得常规的几何交会方法失效。不过,在没有任何偏好信息(也即事先认定哪台经纬仪的测量数据有更可靠的先验知识)的情况下,可以认为飞行器最可能的位置应该处于和这N条射线距离最短的点上。
2.1 目标点M 到经纬仪主光轴的距离
假设有N台经纬仪同时跟踪目标M,为便于利用经纬仪的观测数据解算M的位置,需要构建公共坐标系,如图2 所示。
构建公共坐标系O-XYZ,各经纬仪设备旋转中心Oi在O-XYZ坐标系下的坐标为(X0i,Y0i,Z0i),记 其 与 经 纬 仪 固 有 测 站 坐 标 系Oi-XiYiZi之间转换关系的旋转矩阵是Ri,则不难导出经纬仪i的主光轴在O-XYZ下的直线方程为:

图2 多经纬仪联合观测示意图Fig. 2 Multi theodolite joint observation

利用空间解析几何知识,目标点M(X,Y,Z)到第i台经纬仪的主光轴直线Li的距离可以表示为:

2.2 M 点坐标的最优估计
为融合N台经纬仪的测量数据,尽可能准确地解算目标M的三维坐标,设想M点位于与这N台经纬仪主光轴距离和最小的位置上。由式(2)可以得出目标M到N台经纬仪各自主光轴的距离和,即:
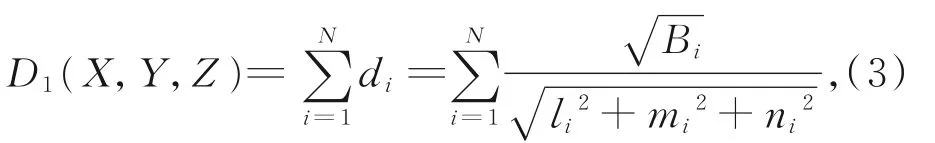
式中:

对于式(3)所表示的极值问题,采用费马引理[10]得到:

由于式(4)是非线性方程组,求显示解困难,本文将式(3)转换为距离平方和:
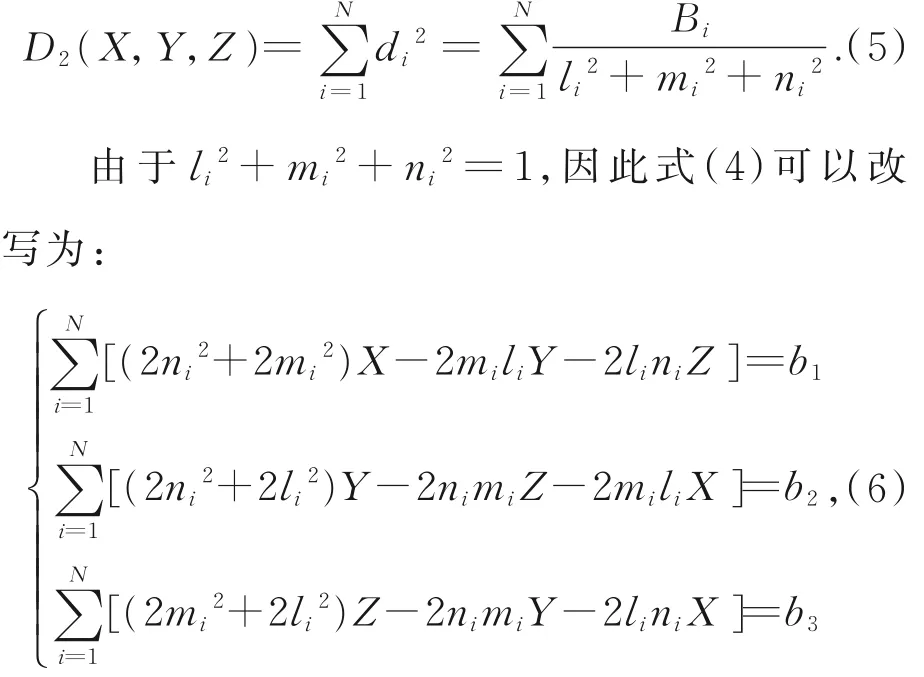
式中:

由三元一次线性方程组式(6),可写出(X,Y,Z)的系数行列式:

显然,C 关于主对角线对称且主对角线上元素不为0,所以C ≠0,则由克莱姆法则[11]可知方程组式(6)有唯一解,且解为:

3 算法改进
多年靶场外测数据处理工作的实践表明,即使是高精度的测量设备,由于多种偶然因素的综合影响或作用,采样数据集合中往往包含(0. 1~0. 2)%的严重偏离目标真值的异常数据[1]。工程领域称这部分异常数据为野值。野值对测角数据交会解算目标位置有着十分不利的影响。因此,本文提出一种自适应容错算法,可在不剔除野值的情况下得到可靠的交会结果。算法流程如图3 所示,具体步骤如下:
(1)假设N台经纬仪获取M在tj( j= 1,2,3,...)时刻的测角数据( A( tj),E ( tj)),在t时刻之前数据无野值,由式(8)计算目标定位坐标,记为:
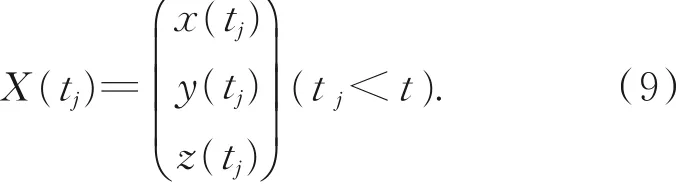
(2)采用多项式拟合外推法[12]对t 时刻之前的定位结果一步外推,得到t 时刻预测结果,记为X^t;
(3)构造Hampel 型[13]函数:

式中c为3~5 倍的σ,σ为测角数据标准差。
(4)利用X^t反算目标相对于N台经纬仪的测角数据,得到反算的方位角和俯仰角数据,记为(A^ti,E^ti);
(5)基于反算的目标相对各经纬仪的方位角和俯仰角数据(A^ti,E^ti),以及式(10)所示的φ函数,构造二维数据:
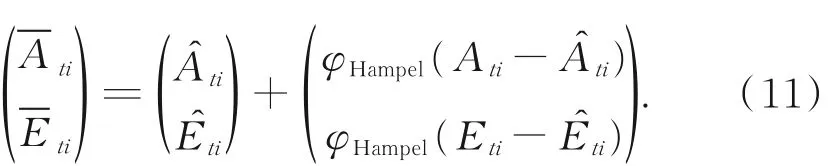

图3 容错定位算法处理流程Fig. 3 Processing flow chart of fault-tolerant location algorithm
4 仿真计算
为验证基于最短距离和的融合定位算法的有效性,并准确评估其性能,本文采用某飞行试验任务部分真实航迹数据作为原始数据。该数据是以地面监控中心某点为公共坐标系原点,采样间隔为0. 25 s,随时间变化的三维坐标数据序列(t,X,Y,Z)如图4 所示。

图4 真实航迹Fig. 4 Real track
已知3 台经纬仪测站的大地坐标,通过坐标转换将真实航迹数据反演至3 个经纬仪测站系下,得到各站测角数据(t,Ai,Ei),部分数据如表1所示。
考虑到大地测量误差、大气折射误差、地球曲率半径等不影响本文算法的有效性,仿真中忽略上述误差的影响。采用Monte Carlo 方法生成均方差为5″的正态分布随机误差序列,叠加到表1 所示的经纬仪方位角数据和仰角数据上,形成随机误差符合正态分布的经纬仪测角数据序列。
利用本文基于最短距离和的融合定位法,以及上述带有正态随机误差的3 台经纬仪测角数据,计算目标航迹(t,X′,Y′,Z′),结果如图5 所示。为了直观地显示算法精度,逐点计算融合定位结果与真实航迹数据的残差(t,ΔX,ΔY,ΔZ),各方向残差如图6 所示。
由图5~图6 可知,3 个方向的定位结果除叠加的随机误差引起的扰动外,目标3 个方向的坐标计算值与真实航迹(图4)完全一致,不存在系统性偏差,从而证明了融合定位算法的有效性。

表1 各站测角数据Tab. 1 Angle measurement data of each station

图5 基于最短距离和的融合定位结果Fig. 5 Result of location fusion based on sum of shortest distance

图6 融合结果与真实航迹残差Fig. 6 Fusion results and real track residual
5 容错仿真计算
对形成的随机误差符合正态分布的经纬仪测角数据序列,采用外部叠加方法形成偏置量不同 的 野 值 点 :(1)A1( 80 )=A1( 80 )- 0.04,(2)A2( 81 )=A2( 81 )- 0.04,(3)E1(180 )=E1(180 )+0.04,(4)A3( 250 )=A3( 250 )- 0.3,(5)E2( 350 )=E2( 350 )+ 0.3,(6)A4( 530 )=A4( 530 )-0.085,(7)E3( 530 )=E3( 530 )+ 0.085,仿真数据如图7 和图8 所示。
对图7 和图8 所示的带多个野值点的仿真数据,分别进行无容错能力的融合定位和有容错能力的融合定位,定位结果分别如图9和图10所示。
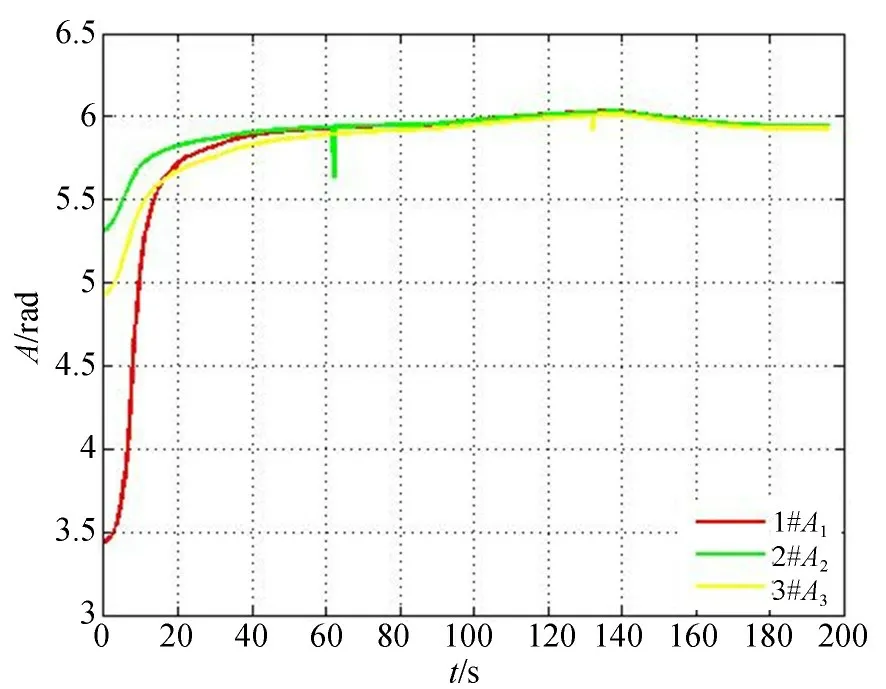
图7 含随机误差和野值的三站方位角数据Fig. 7 Azimuth data of three stations including random error and outliers

图8 含随机误差和野值的三站俯仰角数据Fig. 8 Pitch angle data of three stations including random error and outliers
从图9 和图10 可以看出,3 个方向的定位结果除叠加的随机误差引起的扰动外,无容错能力的融合定位算法得到的结果在各个野值点处都有非常大的偏差,说明野值会严重影响定位算法结果的可靠性;而容错定位算法得到的结果与不含野值的计算结果(图5)基本一致,不存在系统偏差,算法具有较好的抗野值能力。

图9 无容错定位结果Fig. 9 Non fault-tolerant positioning results

图10 容错定位结果Fig. 10 Fault-tolerant positioning results
6 结 论
本文建立的最小距离和容错定位算法既能够充分利用测量数据信息,又可以在不进行野值检验的情况下进行定位计算,确保定位结果不失真。仿真结果表明,该方法对测量数据具有良好的容错能力。当测量数据正常时定位结果达到距离和最小;当测量数据含孤立型野值或长度不超过3 个的斑点型野值时,无需事前修复即可确保定位结果可靠,几乎不受野值影响,能够保证动态目标的实时可靠定位。
