机器人参数辨识和计算力矩法轨迹控制研究*
2021-01-12韩奉林胡金飞
赖 含,韩奉林,胡金飞
(1.中南大学机电工程学院,长沙 410012;2.浙江大学机械工程学院,杭州 310027)
0 引言
随着对机器人运动速度、载荷、轨迹控制精度和稳定性等性能的要求越来越高,单纯基于运动学的机器人轨迹控制方法已不能满足要求,必须在机器人轨迹控制中考虑机器人的动力学特性。
在众多的机器人动态轨迹控制算法中,计算力矩法采用前馈与反馈相结合的控制策略,具有较好的稳定性[1]。目前,针对计算力矩法轨迹控制的研究,一方面为方法论的完善和创新,如刘德满等[2]将计算力矩法和自适应控制相结合;王东署等[3]把神经网络用于计算力矩法,进一步提升实际工业过程的控制精度。另一方面为计算力矩法的工业应用,如梁捷等[4]将计算力矩法用于空间机械臂运动控制,发现该种方法可以节省资源,同时控制精度很高;Sharkawy等[5]展开了两自由度机器人的计算力矩法控制研究;龚捷等[6]研究了基于计算力矩法的装载机工作装置轨迹控制,并针对三维模型进行了控制仿真。
计算力矩法是一种基于动力学模型的控制方法,在机械臂的数学模型及相关参数确定以后,可以实现精确控制。实施计算力矩法控制的前提是需要知道获得机器人惯性参数及关节摩擦状态,但由于制造、装配误差、附属零件等多种原因,上述参数难以直接通过几何设计信息准确测算,往往必须通过在线辨识获取。周军等[7]提出了一种柔性关节模块机器人动力学模型参数辨识方法,苏二虎等[8]进行了考虑电机惯量的机器人动力学参数辨识研究。
为便于计算力矩法的进一步推广应用,本文系统地提出了包括动力学参数辨识、动态轨迹控制在内的完整实施方法,建立了参数辨识和动态轨迹控制的理论模型,并以平面三自由度机器人为例,开展了数值仿真和实验研究。
1 三自由度机器人的运动学和动力学建模
1.1 运动学建模

图1 三自由度机器人模型
平面三自由度机器人在工业中应用广泛,且结构相对简单,是研究动态轨迹控制算法的理想对象。考虑如图1 所示的平面三自由度机器人,运用Danevit-Hartenberg 法[9]建立如图1 所示坐标系,采用图中标识的符号,其中bi(i=1,2,3)指各杆质心据杆前端坐标系沿连杆的距离,lx指偏距,可以得到如表1所示的机器人D-H参数。

表1 三自由度机器人D-H参数
若末端执行器在笛卡尔空间中的位姿由向量(x,y,φ)表示,则(x,y,φ)与θ1、θ2、θ3的关系:

式中:si=sinθi;ci=cosθi;sij=sin(θi+θj);cij=cos(θi+θj);sijk=sin(θi+θj+θk);cijk=cos(θi+θj+θk)。
下面确定x˙、y˙、φ˙与θ˙1、θ˙2、θ˙3的关系:

式中:雅可比矩阵为:

1.2 动力学建模
如图1 所示,令i=1,2,3,设各杆质量为mi,各杆绕质心坐标系(与前一关节坐标系平行但原点位于质心处的坐标系)Z 轴的转动惯量为Ji。考虑实际情况,引入各杆传动装置的等效转动惯量Ii,各关节所受动摩擦力fvi,静摩擦力fci。再利用拉格朗日法建立机器人动力学方程,根据文献[10],动力学方程可线性参数化:

式中: D(θ)为惯性矩阵;C(θ,) 为科里奥利和离心力矩阵; g(θ)为重力项矩阵;f=fvi+fci为关节摩擦力; β 为最小参数集向量,对于本文中的三自由度机器人,动力学参数可整合为15个最小参数集,如表2所示;Y 为最小参数集的系数矩阵,该矩阵的各项元素均为关节变量的函数。

表2 三自由度机器人动力学最小参数集
矩阵D(θ)、C(θ,θ˙)、g(θ)均可表示为最小参数集的线性组合,其中D(θ)为对称矩阵。各矩阵每项元素如下所示:

2 激励轨迹规划和动力学参数辨识
2.1 激励轨迹规划
前文所述动力学模型有未知动力学参数,所以应先辨识出机器人的动力学参数。为降低测量噪声的影响,使辨识出的数据更加准确,需先优化激励轨迹。文献[11]表明,每个关节的激励轨迹可为N个谐波正弦和余弦函数的有限和。

式中:ωf是傅里叶级数的基频,周期Tf=2π/ωf,所有关节基频相同,以保证整个机器人激励的周期性。每个关节的激励轨迹包含2N+1个参数,正、余弦函数的幅值以及位置轨迹的偏移量ci。
根据式(4),对于第n个样本点,动力学方程可写为:

若共有m个样本点,动力学方程可写为矩阵形式:



图2 激励轨迹位移图

图3 激励轨迹速度图

图4 激励轨迹加速度图
2.2 参数辨识实验

图5 实验中采用的柯马Racer3机器人
柯马Racer3 机器人当关节1、4、6 锁定于零位,关节2、3、5 运动时与图1 所示的三自由度机器人同构,因此后续将以此机器人为平台进行实验,如图5所示。柯马Racer3 机器人采用了贝加莱系统,编程环境为Automation Studio,支持IEC 61131-3语言和C 语言。首先,以0.8 ms为周期对激励轨迹进行采样,将30 s 内的采样数据导入实验系统,在机器人各关节回零后进行不基于动力学的PID 控制实验。实验过程中,由电枢电流可实时计算出关节的实际力矩,由关节编码器可得出实时位置数据。实验结束后,在Automation Studio的function block中读取各样本点的力矩和位置数据,并进行滤波处理,将滤波后的位置数据进行一阶差分、二阶差分得到速度和加速度值。由式(7)可得:

将滤波后的力矩、位置、速度、加速度数据代入式(9),参数辨识结果如表3所示。

表3 参数辨识结果
利用辨识出的参数值,结合实际轨迹数据,根据动力学公式计算出理论力矩,和实际力矩的对比如图6~8 所示,两力矩值吻合程度较高。由于低速情况下,摩擦力的影响更为显著,故力矩误差在每次关节速度为0时会出现峰值。所以将实际力矩中速度低于0.007 rad/s的样本点剔除,计算剩余样本点的力矩误差的均方根值,依次为1.9243 N·m、1.5922 N·m、0.5999 N·m,较小的均方根值说明了数据的稳定性,也说明了各采样点误差集中分布在零附近,证明了参数辨识的准确性。

图6 关节1力矩误差

图7 关节2力矩误差

图8 关节3力矩误差
3 计算力矩法控制理论
计算力矩法是对机器人的非线性化模型进行补偿,从而实现线性化控制。机器人的动力学方程如式(4)所示。


通常为实现关节间的解耦,Kd和Kp选择为正定对角矩阵[12]。联立式(4)、(10)、(11)可得:

由于Kd、 Kp为正定矩阵,则是全局渐近稳定的平衡点,即最终收敛于
计算力矩法的完整控制输入如下:
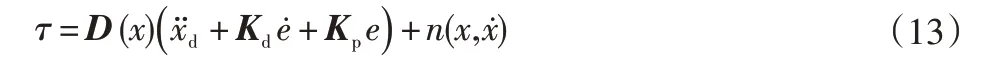
控制框图如图9所示。

图9 线性化逆动力学控制框图
4 轨迹跟踪仿真和实验
4.1 计算力矩法控制仿真
在Simulink 环境中,利用表3 的参数辨识结果,按照图9建立三自由度机器人的运动学、动力学及控制系统仿真模型。
为更好地模拟实际机械臂运行情况,机器人主体程序中考虑一定程度的白噪声。设置仿真时间为30 s,采样时间为0.001 s,经反复地调试,得到较好的控制器参数Kd和Kp分别为diag(6,6,5.15)、diag(250,250,195.48),三自由度机器人各关节的仿真结果如图10~12所示。
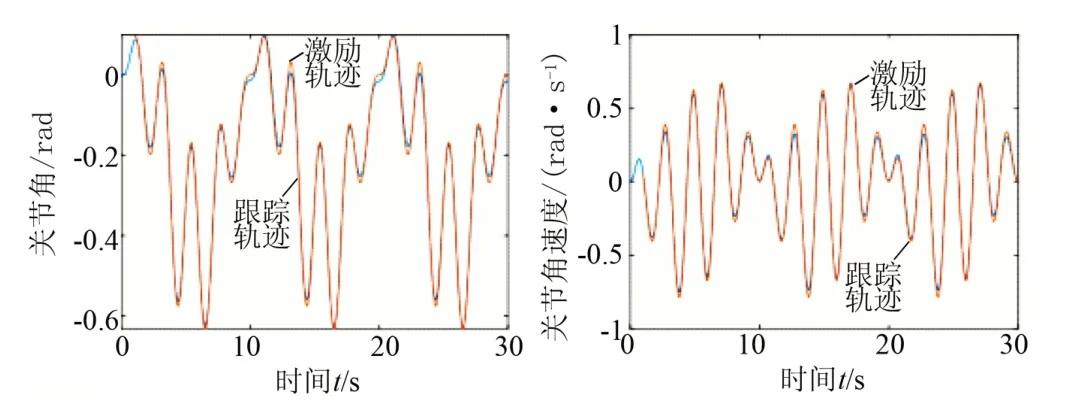
图10 关节1的动态轨迹跟踪仿真结果

图11 关节2的动态轨迹跟踪仿真结果

图12 关节3的动态轨迹跟踪仿真结果
4.2 计算力矩法控制实验
上述仿真结果表明,基于动力学的计算力矩法能取得较好的控制效果。采取反复调试所得的控制器参数Kd和Kp,展开以下计算力矩法控制实验。
类似辨识实验,仍利用柯马Racer3 机器人同平面的3 个关节,以激励轨迹为控制输入,进行计算力矩法控制实验。实验结果滤波处理后,各关节的位置跟踪结果如图13 所示。对比输入轨迹和实际轨迹,跟踪误差如图14所示。由于作为控制输入的激励轨迹加速度较大,实验过程中会引发相对更大的振动,导致一定程度的轨迹跟踪误差,各关节的最大跟踪误差依次为0.0227 rad、0.0119 rad、0.0064 rad。关节1相较于关节2、3整体速度更小,受摩擦力的影响更大,而且根据表3的辨识结果,关节1所受摩擦力是最大的,所以关节1的跟踪误差相对更大。但总体而言,各关节误差在0附近的小范围内波动,稳定可控,说明计算力矩法实现了较高精度的轨迹跟踪控制。

图13 各关节的位置跟踪结果
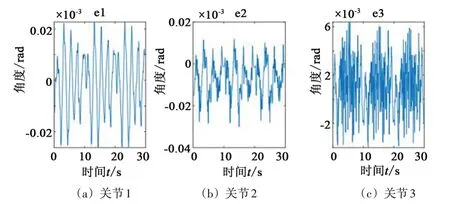
图14 各关节的位置跟踪误差
5 结束语
本文建立了三自由机器人的运动学、动力学模型,并借助柯马Racer3 机器人2、3、5 关节进行了动力学参数辨识实验,再对基于动力学模型的计算力矩法展开了轨迹跟踪仿真和控制实验,得出以下结论。
(1)以谐波正弦和余弦函数的有限和作为激励轨迹,并对其系数优化以减小噪声的影响,再进行不基于动力学的PID辨识实验,能够实现机器人动力学参数的准确辨识。
(2)在准确的参数辨识基础上,计算力矩法控制实验的结果表明,该种方法能够实现机器人较高精度的轨迹控制,具有很好的应用前景。
