基于有限元法的网式自然干燥储仓结构设计*
2021-01-12王会铭
王 英,王会铭,白 朋,余 飞
(张掖市誉宇农业机械科技有限责任公司,甘肃 兰州 734000)
0 引 言
玉米制种产业作为“十三五”期间国家的重要战略决策,根据以玉米种植为重点稳步推进供给侧结构性改革的政策,着力解决玉米制种产业发展面临的专业化、科学化、集约化发展水平不足问题,研发一种网式自然干燥储仓。 针对目前玉米种子制种产业普遍存在田间基础设施不完善,农业机械化程度不高,尤其是玉米果穗晾晒场地有限,晾晒设施、果穗及子粒烘干设备不足,导致玉米果穗不易干燥,干燥周期长,遇恶劣天气,采收时种子霉变,影响发芽率,给制种企业和农户造成严重损失;而使用干燥剂、机械干燥等方式,则会大大增加制种成本。因此,此研究成果即一种网式自然干燥储仓,可以保证玉米果穗的自然条件下干燥,同时占地面积小,避免恶劣天气所带来的损失,代替了地面铺放晾晒的落后方式。在此网式自然干燥储仓设计中,关系整体设备安全和运行稳定性的重要设计要求是整体结构设计强度、刚度是否满足要求。
笔者通过采用有限元方法[1],在设计过程中,模拟实际工况,对储仓添加约束,施加载荷,包括自重、玉米重量、风载、雪载等,对组成储仓的直立式容器、仓下支撑结构、加强筋、卸料装置进行了强度、刚度校核。该方法对优化网式自然干燥储仓结构设计、简化设计校核流程、缩短研发周期、节省研发成本有着重大的意义。
1计算模型及仿真方法
1.1计算模型
文中所述的网式自然干燥储仓,在其额定工作状态下,设计性能及主要结构参数见表1所列。

表1 网式自然干燥储仓主要参数
根据设计意图,绘制网式自然干燥储仓的二维设计图,其结构如图1所示。
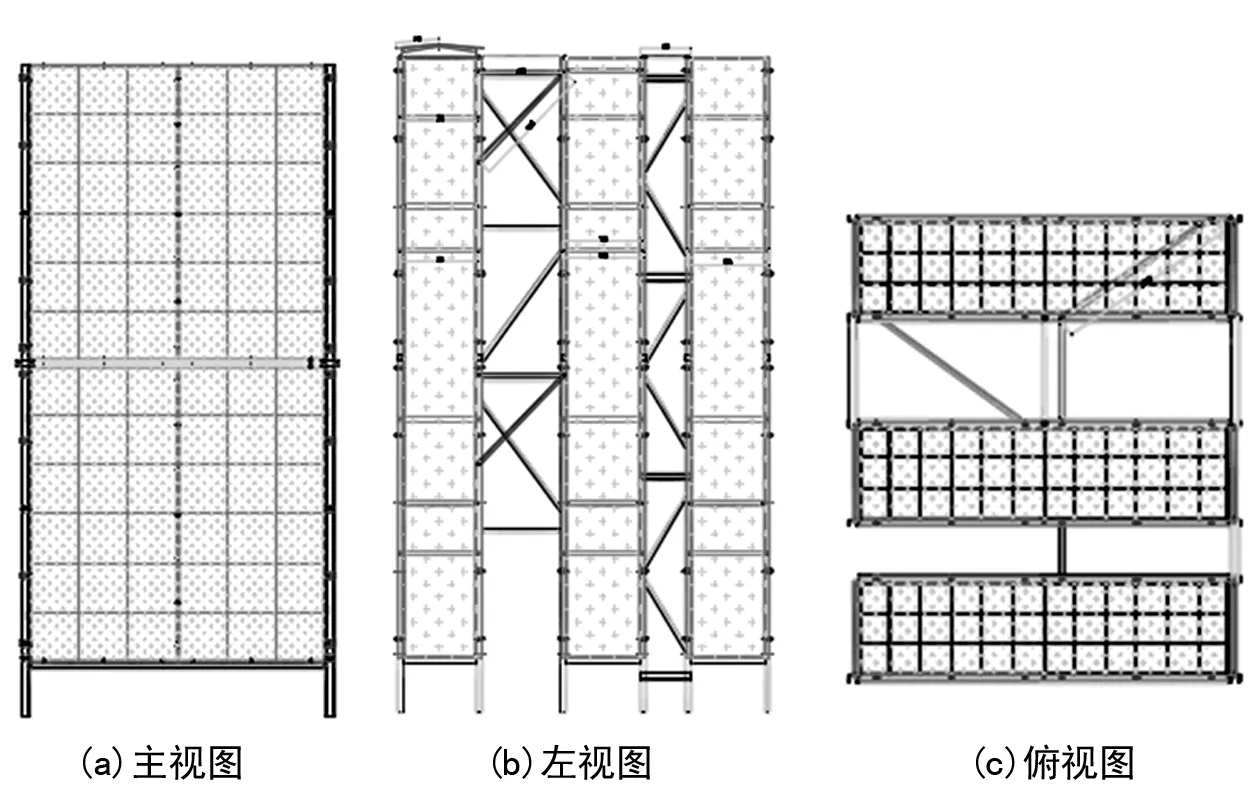
图1 网式自然干燥储仓二维设计图
根据图1所绘制的二维图纸,使用SolidWorks三维建模软件,对网式自然干燥储仓的结构件进行三维建模,并对模型进行处理,获得能够适用于有限元计算的三维模型。自然干燥储仓计算模型如图2所示。

图2 网式自然干燥储仓计算模型
1.2 计算模型网格划分
在进行有限元软件进行仿真分析前,首先需要对计算模型进行离散,即采用前处理软件,对其进行网格划分。由于计算对象为固体结构,且整体结构较为复杂,网格划分采用非结构型网格划分形式[2],为了提高计算精度,对局部网格进行了加密,网格输出类型匹配有限元求解器,全模型共有553548个计算节点,162434个网格单元。网式自然干燥储仓计算部分网格划分结果如图3所示。
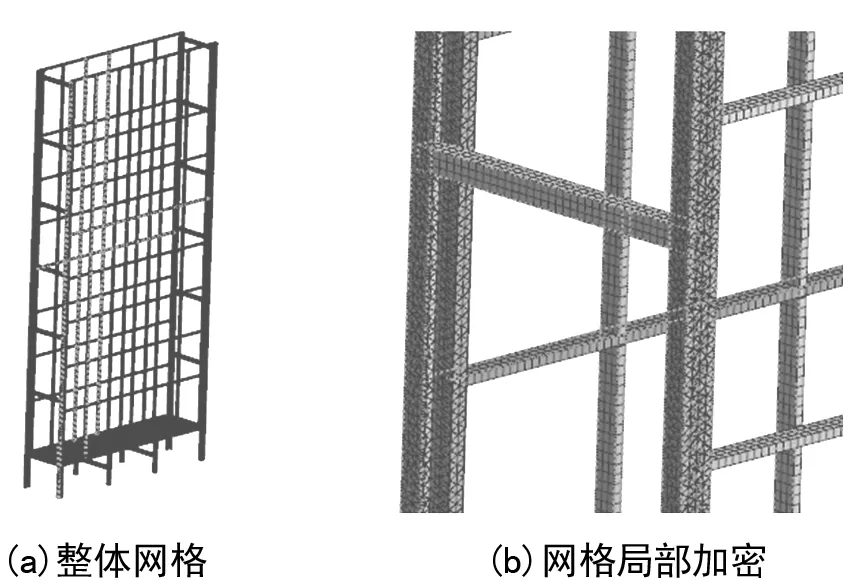
图3 网式自然干燥储仓计算部分网格划分
1.3 计算工况
对于网式自然干燥储仓结构分析,其工况为静止状态下,结构体所受载荷对整体产生的应力,以及该应力引起的应变。分析中采用静力学结构求解模型对该问题进行计算。网式自然干燥储仓结构体所受的主要载荷包括:储仓自重、所储存干燥玉米种子重量、基本风压及基本雪压载荷。在进行强度、刚度校核时,考虑极限工况,即在以上几种主要载荷共同作用条件下,对整体结构进行求解计算。
根据伯努利方程[3],计算风载对装满玉米后,网式自然干燥储仓的最大风压载荷为:
(1)
式中:F为风对网式自然干燥储仓迎风面的作用力,kN;A为迎风面积,m2;r为空气重度,kN/m3;v为风速,m/s;g为重力加速度,m/s2。
根据式(1)所示,当网式自然干燥储仓迎风面为宽6 m,高3 m时,风对整体结构的作用力存在最大值;通过查阅风力等级与风速对照表,当风力等级为11级时,即仅次于台风等级的条件下(风速为28.5~32.6 m/s,取30 m/s为计算值)时,网式自然干燥储仓所受的最大风载约为9.9 kN。
在雪压载荷计算时,通过查阅全国的基本雪压分布[4],50年一遇最大雪压取偏大值0.7 kPa。由于网式自然干燥储仓顶部为平面,且长度为6 m。宽度为0.8 m,则网式自然干燥储仓所受的最大雪压载荷为3.36 kN。
1.4 边界条件
在网式自然干燥储仓结构分析计算过程中,其材料为Q235,具体材料特性如下:密度为7 850 kg/m3;泊松比为0.3;杨氏模量为200 GPa;抗拉屈服强度为250 MPa;极限应力强度为469 MPa。储仓底座通过地脚螺栓与地基连接,因此计算时在相应位置处添加固定约束;在设计工况下,储仓能够容纳的玉米重量为6 500 kg,在此结构下,根据三角函数,计算获得储仓内玉米对储仓内壁向外的作用力为4.33 kN;在极限工况所受的风载为9.9 kN;所受最大雪压载荷为3.36 kN,同时考虑储仓结构自身重量在重力势能作用下对支腿的作用力。网式自然干燥储仓结构约束及载荷加载情况如图4所示。
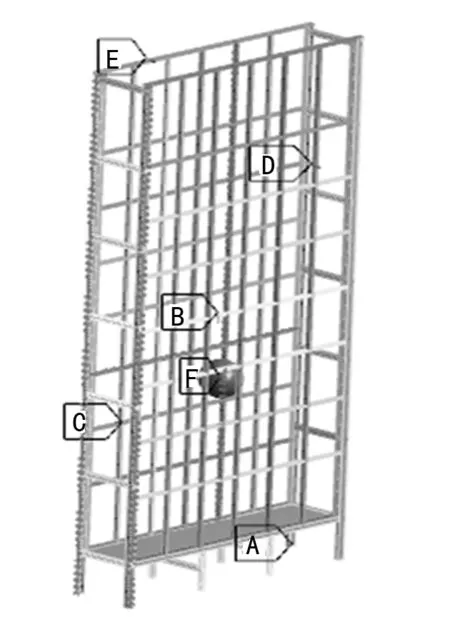
图4 网式自然干燥储仓结构约束及载荷加载状态
图4中,A为固定约束;B为重力势能的作用力的方向和大小;C、D为储仓内玉米对储仓内壁向外的作用力;E为风载的最大值对储仓迎风面的作用力;F为储仓内玉米的自重和雪载在储仓顶部的自重之和。
2 计算结果与分析
将前处理器划分的网格导入有限元求解器,采用静力学计算模型,按照上述的约束条件和载荷类型添加边界条件,对网式自然干燥储仓结构进行强度、刚度计算分析。通过计算,获得网式自然干燥储仓结构的应力云图如图5所示。
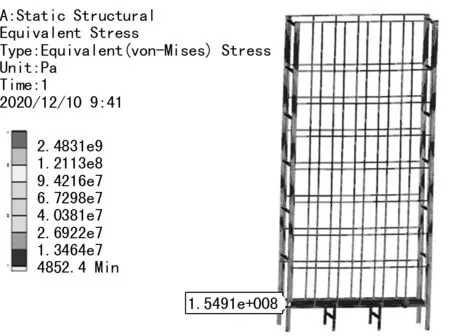
图5 网式自然干燥储仓结构的应力云图
从图5可以看出,网式自然干燥储仓结构整体应力的最大值出现在底部基座处位置,忽略应力集中效应,应力最大值为155 MPa。此应力分布状态为储仓在装满玉米种子,且在风载和雪载的最大值共同作用下的结果,且最大值小于材料的许用应力。
在求解储仓应力分布状态的基础之上,进一步计算获得网式自然干燥储仓结构整体应变状态,获得网式自然干燥储仓结构整体应变云图,如图6所示。

图6 网式自然干燥储仓结构的应变云图
从图6可以看出,网式自然干燥储仓结构的应变的最大值为3 mm,位于网式自然干燥储仓结构的迎风面竖直支撑杆处,同样,此应变的分布状态也是在储仓处于满负荷,且最大风载、雪载共同作用的情况下。综合应力和应变的分布状态云图,可以判断,此网式自然干燥储仓结构的强度和刚度均能够满足设计要求。
3 结 语
采用有限元分析的方法,对网式自然干燥储仓的主体结构在设计定型阶段进行强度、刚度校核计算分析。在绘制二维图纸的基础上,进行了储仓主体结构三维模型建模并获得可用于有限元计算的计算模型,采用前处理软件进行计算模型的离散,并获得网格数据文件。为保证设计满足强度要求,查阅资料,计算获得所受风载和雪载的最大值作为计算分析的边界条件,同时按照实际工况,添加约束条件,通过计算分析,获得了该型网式自然干燥储仓的主体结构应力与应变的云图。结果表明:网式自然干燥储仓的主体结构应变的最大应变为3 mm,应力的最大值为155 MPa,小于材料的许用应力。因此,此储仓的主体结构能够满足极端气候条件下,额定工作状态的工作要求。
通过研究所述方法,在网式自然干燥储仓结构强度、刚度校核计算时,全面考虑风力载荷和雪载对储仓整体结构的作用力,保证计算结果能够更加符合实际工况的条件。通过获得应力、应变的分布云图,直观反映计算结果。该方法对设计人员优化储仓结构设计提供了新的手段,相较于传统设计方法,能够极大的缩短设计周期,减少研发成本。
