八自由度蒸发器检修机器人设计及运动分析*
2021-01-12王湘江冯栋彦
王 宠,王湘江,冯栋彦
(南华大学 机机械工程学院,湖南 衡阳 421009)
0 引 言
随着核电行业的蓬勃发展,核电站的安全问题得到人们的普遍关注。为保证核电站运行安全,需要定期对核电站关键设备进行检查检修。其中,蒸汽发生器检修时核电站检修的重要步骤[1-2],检修期间,为了防止异物通过与主管道直接相连的蒸汽发生器进入堆芯,要在蒸发器堵口一端安装堵板,以便将蒸汽发生器与主管道进行隔离。现阶段堵板拆装人工操作存在工作效率低、环境辐射剂量高、空间狭小、安装精度偏低等问题[3],各国已有检修机器人的功能和作业能力各不相同,检修机器人的研发仍然面临较大问题。首先,由于核电行业的特殊性,各国之间技术交流有限,对外公开的资料也十分少:其次,受蒸汽发生器结构和作业环境的影响,检修机器人的安装和工作受到很大限制,这对机器人的设计提出了更高的技术要求[4]。
针对某型蒸汽发生器堵板安装要求,笔者提出一种8自由度的堵板拆装机器人。机器人以一种6自由度协作机械臂为本体,通过加装两个伺服电缸,增加一个平移自由度,一个旋转自由度,使机器人本体可以更加灵活的到达工作位置,增加机器人工作范围。利用 D-H 参数得到机械臂的关节变换矩阵,通过矩阵连乘得到运动学正解;运动学逆解;最后利用matlab软件中的工具箱 Robotics Toolbox 进行运动仿真[5]。从而为机器人的实际工作提供理论依据,避免作业过程中可能出现的风险,确保堵板拆装工作顺利完成。
1 八自由度机器人运动学分析
1.1 运动模型的建立
蒸发器模型如图1所示。八自由度串联型工业机器人本体可以看作是不同特征的连杆所构成的一个复杂的多刚体系统空间结构,如图2所示。在运动分析过程中,利用D-H参数法可确定用于表示连杆本身特征,以及表示连杆与相邻杆之间连接关系的四个参数:杆件长度、杆件扭角、关节距离、关节转角。

图1 蒸发器模型及安装环境1.主管道 2.地脚 3.人孔
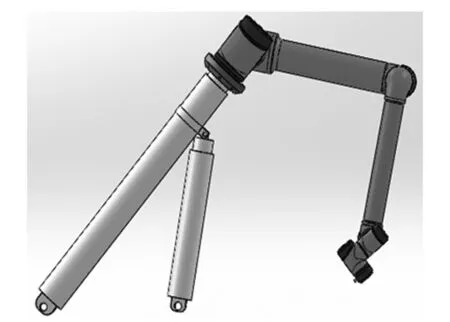
图2 八自由度机器人模型
1.2 正运动学分析
此研究描述的八自由度机器人拥有7个旋转自由度,一个平移自由度 ,采用D-H参数法建立运动模型时,为了更加方便的理解各个连杆运动情况,建立起如表1对应的D-H参数表[6],为准确描述,需要明确其中四个参量:连杆长度ai,连杆夹角αi,连杆偏距di,关节角θi。

表1 机器人D-H 参数
机器人的正运动学即给定关节转动角度求解机器人末端位置和姿态的过程,根据公式:
(1)
可得机器人各个关节变换矩阵为:
(2)
由上式可得机器人末端位姿相对于机器人基坐标系矩阵变换矩阵为:
(3)

1.3 逆运动学分析
机器人逆运动学是已知机器人末端坐标系相对于基坐标系的相对位姿,如何得到满足相对位姿的关节变量,是笛卡尔空间向关节空间的转换[7]。
得到机器人逆解的方法,是使运动方程式两端逐步左乘各矩阵的逆矩阵,并使两边相等矩阵对应元素相等,从而得到该过程各个关节的变量。
同样使用i-1T8表示连杆8的坐标系与连杆i-1坐标系的关系[8,9]:
(4)
求解关节变量方程式如下:
A1-1T=1T8
A2-1A1-1T=2T8
A3-1A2-1A1-1T=3T8
A4-1A3-1A2-1A1-1T=4T8
A5-1A4-1A3-1A2-1A1-1T=5T8
A6-1A5-1A4-1A3-1A2-1A1-1T=6T8
A7-1A6-1A5-1A4-1A3-1A2-1A1-1T=7T8
(5)
2 轨迹规划仿真
使用Matalab中的轨迹规划函数进行关节空间和笛卡尔坐标空间轨迹规划[10]。轨迹规划仿真利用两个函数:
(1) jiraj函数,已知开始和结束的关节角度,使用五次多项式进行轨迹规划。
[q,qd,qdd]=jtraj(q0,qf,m)
(2) ctraj函数,已知开始和结束的末端关节位姿,利用匀加速、匀减速运动来规划轨迹。
Tc=ctraj(T0,T1,n)
其中:m、n为插值次数。
通过上述函数调用的叙述,采用以上函数进行实例仿真。可以直观地得到工具端沿着直线(见图3)从p1点运动到p2点,同时还可以得到机器人8个关节在整个运动过程中的位置、速度和加速度。由以上理论,通过matalab中的机器人工具箱对机器人进行轨迹规划。
图3 直线轨迹
在本次轨迹规划仿真中得到的第一个点为机器人所默认的零点位置p1,此点在空间直角坐标系中的坐标为(1.02,1.95,1.04),单位为m。工具端到达本次轨迹规划中点为p2,坐标为(1.94,0.02,2.48))单位为m。通过对比直线轨迹位置和各关节运动范围,可以确定直线位于工作空间内。最后利用上述函数得到机器人从开始到结束过程中8个关节角的位置(见图4)、速度(见图5)和加速度变化曲线(见图6)。

图4 关节位置变化曲线
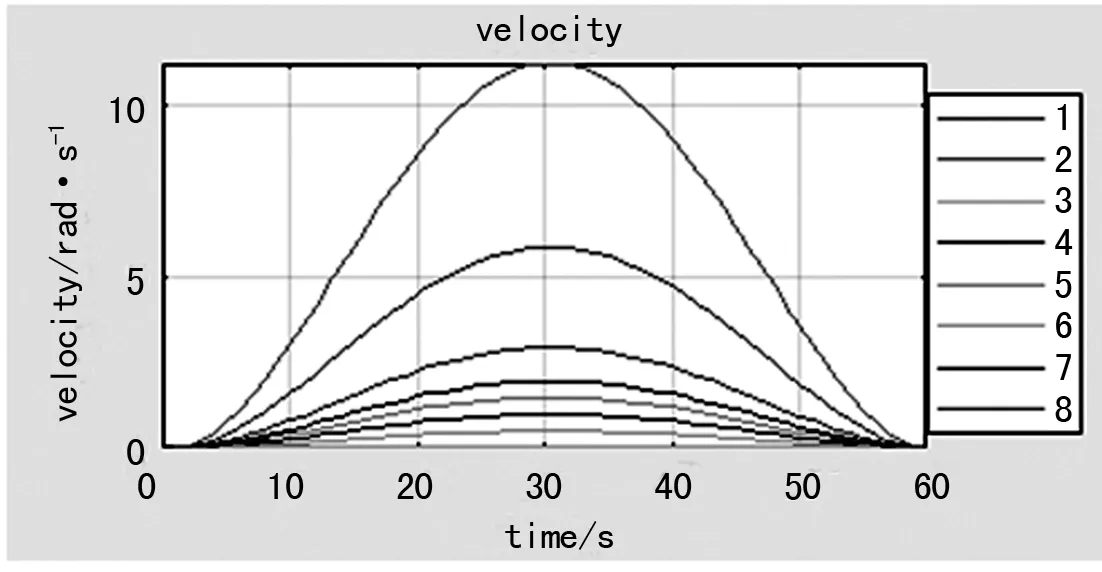
图5 关节速度变化曲线
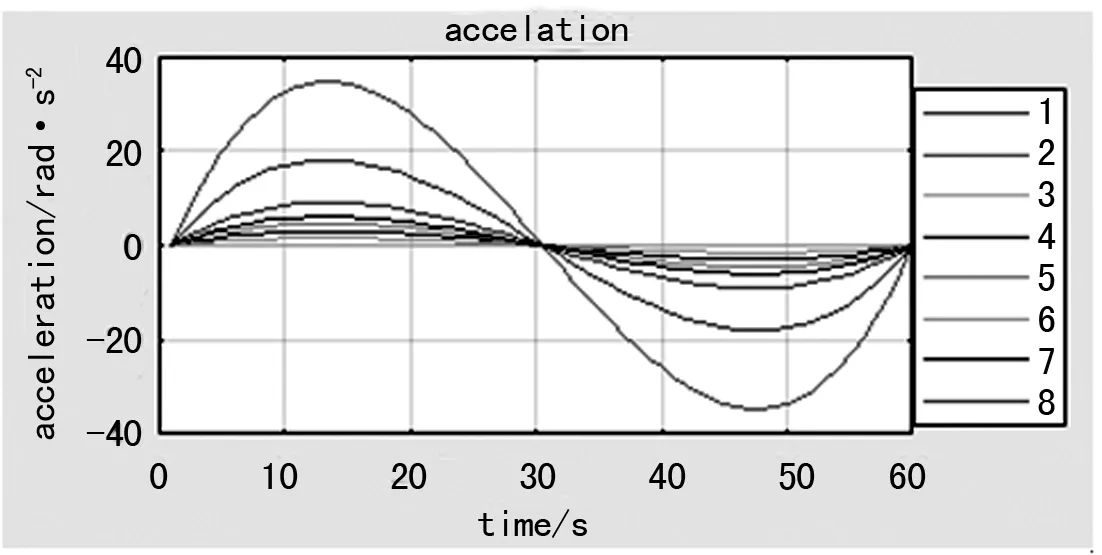
图6 关节加速度变化曲线
根据机器人运行过程中角度、角速度和角加速度随时间变化的过程,可以得出以下结论:
(1) 角度变化曲线光滑,易于控制。关节速度变化先增后减,并在30 s左右达到最大。加速度曲线呈S型分布,先正后负,在30 s左右角加速度都为0.
(2) 针对角加速度30 s附近,各个关节加速度为0,可以看做这个点为“过渡”点,机器人八个关节从起点收到正向驱动力矩,速度逐渐增加,到达“过渡”点时要考虑到达终端时平稳停止,所以在此点开始施加反向力矩,从而逐渐减小加速度至0。
3 结 语
针对蒸汽发生器堵板拆装的实际需求,设计具有八自由度的堵板机器人本体结构,基于连杆D-H参数坐标系,建立其运动学正逆方程并进行求解;在matalab中建立机械臂运动模型,在机械臂上进行轨迹规划仿真,结果显示在设定范围内机器人运行正常,为堵板拆装机器人方案提供了重要论证,为通过使用机器人代替传统人工作业,从而提高整个堵板拆装过程中的安全与效率问题提供了重要理论依据。
