天线支座方位轴瞬态动力学分析*
2021-01-12张学蓉唐先春蒋辛辉
文 广,程 明,张学蓉,唐先春,蒋辛辉 李 航
(1.成都工业学院 智能制造学院,四川 成都 611730; 2.成都无线电专用设备厂(国营633厂),四川 成都 611730)
0 引 言
方位轴是天线支座系统的重要组成部分,天线的方位调整功能主要依靠其来实现。在天线执行搜索功能时,方位轴会带动轴上的零件做往复旋转运动,在此过程中,方位轴主要承受周期性的扭转载荷。由于动力不稳定、安装存在误差等原因,方位轴承受的扭转载荷数值会随时间发生变化。因此,分析方位轴在动载荷作用下的应力响应特性,对方位轴的结构设计而言十分必要。在过往的工程结构设计分析实践中,存在着大量的瞬态特性分析案例。文献[1]在考虑迟滞效应的前提下对某水泵水轮机进行了瞬态动力学分析。文献[2]通过对某强夯机臂架进行静态和瞬态动力学分析,发现了臂架折弯的真实原因。文献[3]利用有限元软件对某减速器输出轴在冲击载荷作用下的瞬态响应进行了分析。文献[4]通过动力学仿真和瞬态动力学分析研究了某采煤机液压拉杆在动载荷作用下的应力和变形。文献[5]利用Ansys仿真平台模拟了某复合刀具在加工过程中的受力变形,获取了刀具的最大应力及部分关键点的径向位移变化情况。文献[6]以某深海高压模拟装置的压力筒为研究对象,借助有限元瞬态动力学仿真模块对其动态响应进行了分析,获取了筒体的应力分布情况。文献[7]通过建立某桥梁伸缩装置的参数化模型,利用有限元软件对其进行了瞬态动力学分析,得到了结构在不同车速和不同载荷下的应力响应情况。文献[8]利用有限元瞬态分析技术对某托架在传感器标定过程中的应力和变形响应进行了研究。文献[9]则以某地铁列车转向架构架为对象,利用有限元软件对其开展了瞬态动力学分析,找出了结构的薄弱环节。文献[10]通过仿真分析手段对某液压挖掘机的动臂和斗杆进行了瞬态动力学分析,获得了结构的应力变化规律。从上述文献分析来看,有限元仿真分析手段是对结构进行瞬态动力学研究的有效方法,并且得到了广泛的应用。笔者利用有限元软件Ansys的瞬态动力学分析模块,对某天线支座方位轴在工作载荷作用下的瞬态响应进行研究,分析结果为该方位轴的结构优化提供了理论依据。
1 方位轴结构示意及受力状况
方位轴是雷达天线支座的重要组成部分,主要用于调节确定雷达的方位。其结构示意如图1所示,该方位轴为阶梯轴,工作过程中主要承受电机启动带来的扭矩。该轴由Q345钢制成,其材料特性参数如表1所示,该材料的屈服强度为345 MPa,进行强度校核时,引入安全系数1.34,则材料的许用应力为257 MPa。
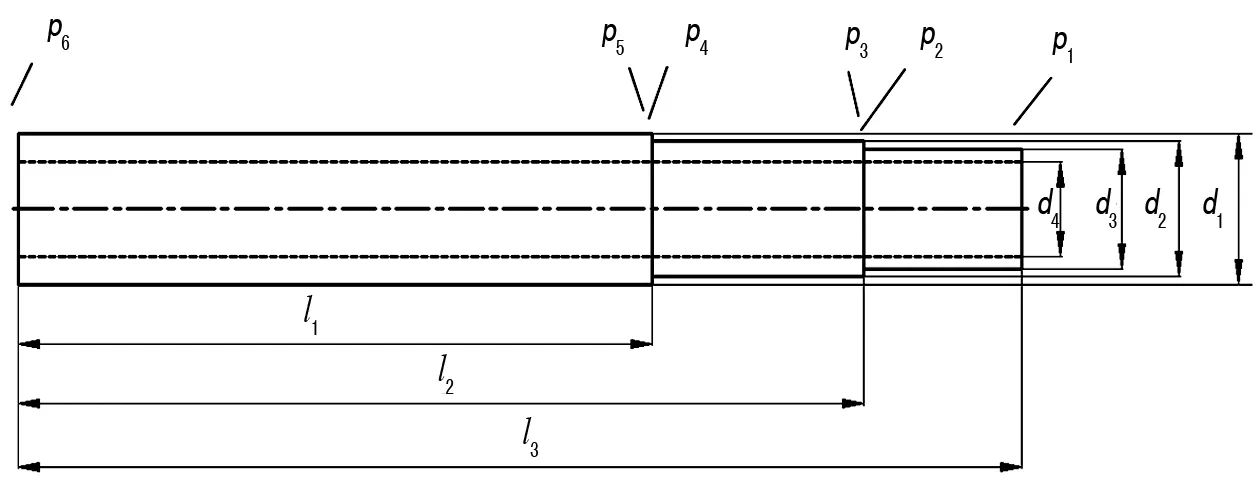
图1 方位轴结构示意图

表1 Q345材料特性参数
2 方位轴瞬态动力学分析
2.1 建立方位轴有限元模型
分析之前,根据该方位轴的实际模型,在忽略轴肩处的倒角等结构后,利用有限元软件Ansys建立其有限元模型。考虑到该方位轴形状较为规则,采用Solid45单元来模拟该轴,选用扫掠网格划分方式对其进行网格划分,整轴被离散成23 968个单元,共有29 816个节点。本次建模采用参数化编程语言来实现,部分建模程序如下:
/prep7
ex=2.1e5
prxy=0.3
den=7.85e-6
et,1,solid45
mp,ex,1,ex
mp,nuxy,1,prxy
mp,dens,1,den
/prep7
csys,0
k,1,,,,
k,2,,,d12/2
k,3,,,d11/2
......
vrotat,all, , , , , ,1,14,360,8,
该方位轴有限元模型如图2所示。
2.2 方位轴瞬态动力学分析结果
完成该方位轴的有限元模型后,根据方位轴的实际工作情况对其约束和加载。方位轴在工作过程中主要承受扭转载荷,分析时,以在方位轴顶端施加均布力偶的形式来模拟方位轴承受的扭矩,通过约束其底面来模拟其他零件对其安装面的约束,方位轴自身的重力则通过施加重力加速度来模拟。约束和加载后的有限元模型如图3所示。
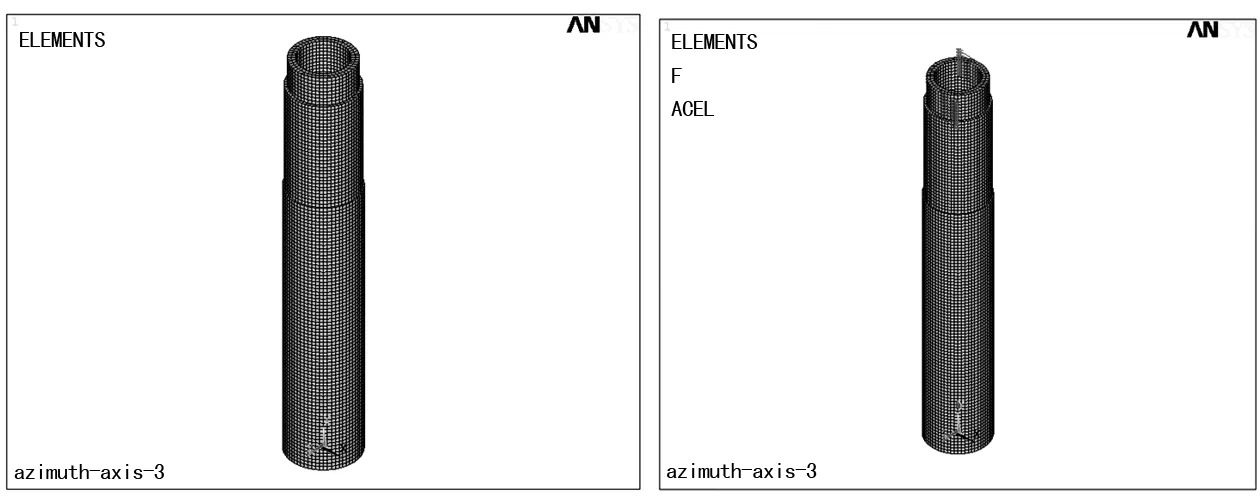
图2 方位轴有限元模型 图3 约束和加载后的方位轴有限元模型
文中主要分析方位轴在完成一个运动周期,即转动一周过程中的瞬态响应。当方位轴的转速为nrad/s时,方位轴转动一周所需的时间为1/ns。以t=t0=0时刻为方位轴转动的初始时刻,假设t=t1= 39/(80×n) 时,方位轴承受到一定数值的冲击载荷(设冲击载荷系数为x,静态时,方位轴承受的扭矩大小为T0,则冲击载荷大小T1=x×T0)。方位轴在1/ns内承受的动载荷随时间变化的曲线如图4所示。

图4 方位轴承受的时间历程载荷示意图
此次瞬态动力学分析采用完全法,考察方位轴轴肩部位关键点(如图1所示)的瞬态响应,分析结束后,提取轴肩部位关键点(分析点)的应力随时间变化的曲线。为了更加全面地研究该方位轴的动态特性,文中考察了不同冲击载荷大小和不同转速下的方位轴瞬态响应变化情况。
(1) 不同冲击载荷大小下的方位轴瞬态动力学分析结果
冲击载荷的大小通过改变冲击载荷系数来获得,本文分析了冲击载荷系数x分别为1.4、1.6、1.8,转速n=2时,方位轴的瞬态响应。图5~7分别给出了冲击载荷系数x分别为1.4、1.6、1.8时,各分析点的应力随时间变化曲线。

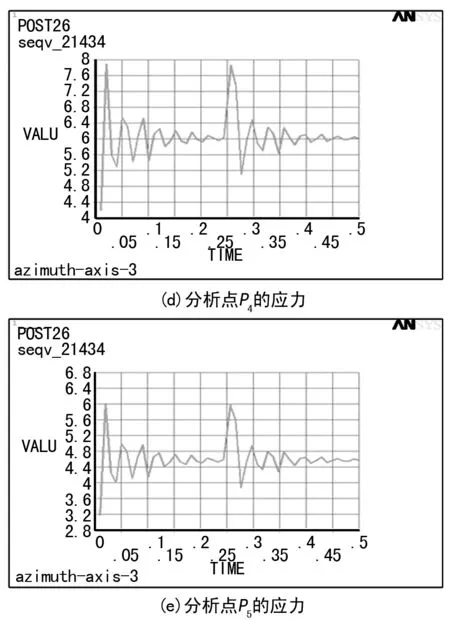
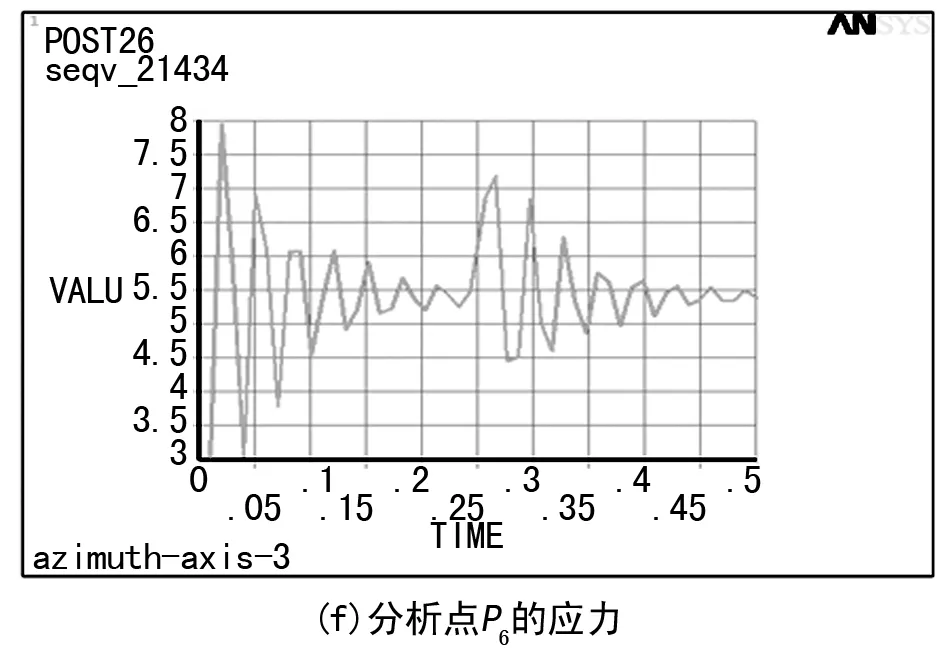
图5 关键点的应力随时间变化曲线(x=1.4)
从图5(a)可以看出,在该方位轴的分析点P1处,其应力-时间曲线出现了两个较大的峰值,分别位于t=0.02 s和t=0.256 25 s时刻,分别对应加载的初始时刻和冲击载荷离开的时刻。从图5(b)~(e)可以看出,在分析点P2、P3、P4、P5处,其应力响应曲线也出现了两个较大峰值,这两个峰值同样位于加载的初始时刻和冲击载荷离开的时刻。从图5(f)可以看出,在该方位轴的分析点P6处,其应力响应曲线的峰值较多,第一个峰值出现在加载的初始时刻,第二个较大的峰值出现的时刻与冲击载荷离开的时刻相比,稍微有点滞后,滞后的时间非常短暂,基本上可以忽略不计。总体来看,图5反映出的六个分析点的应力响应曲线均出现了两个较大的峰值,均出现在载荷突变的时刻,这是由于载荷突变时,产生的冲击效应所致。另外,从图5也可以看出,上述六个分析点中,分析点P2的应力最大,其最大值约为14 MPa,远小于材料的许用应力,可以认为,当冲击载荷系数为1.4时,该方位轴的强度能够满足使用要求。
从图6(a)~(e)可以看出,当冲击载荷系数为1.6时,在分析点P1、P2、P3、P4、P5处,其应力响应曲线也出现了两个较大的峰值,分别出现在加载的初始时刻和冲击载荷离开的时刻。从图6(f)可以看出,当冲击载荷系数为1.6时,在分析点P6处,其应力响应曲线的峰值较多,第一个峰值出现在加载的初始时刻,第二个较大的峰值出现的时刻略微滞后于冲击载荷离开的时刻。


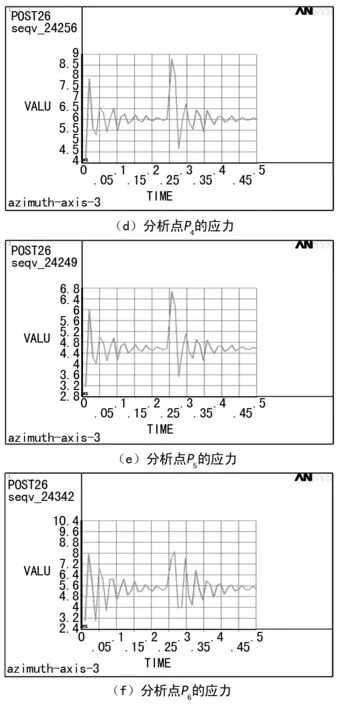
图6 分析点的应力随时间变化曲线(x=1.6)
从图6也可以看出,当冲击载荷为1.6时,各分析点的应力响应曲线表现出的规律和冲击载荷为1.4时的情况一致。另外,当冲击载荷系数为1.6时,应力最大值也出现在分析点P2处,因此,后续分析也只围绕分析点P2展开。
从图7可以看出,当冲击载荷系数为1.8时,分析点P2的应力响应曲线中的两个较大峰值也位于加载的初始时刻和冲击载荷离开的时刻,曲线表现规律和图6、图7相同。从图7、图5(b)、图6(b)对比可以看出,随着冲击载荷系数的增加,即冲击载荷的增大,分析点P2处的最大应力值也会增加,但是,其最大值均未超过材料的许用应力,因此,可以认为在当前冲击载荷工况下,材料的强度能够满足使用要求。
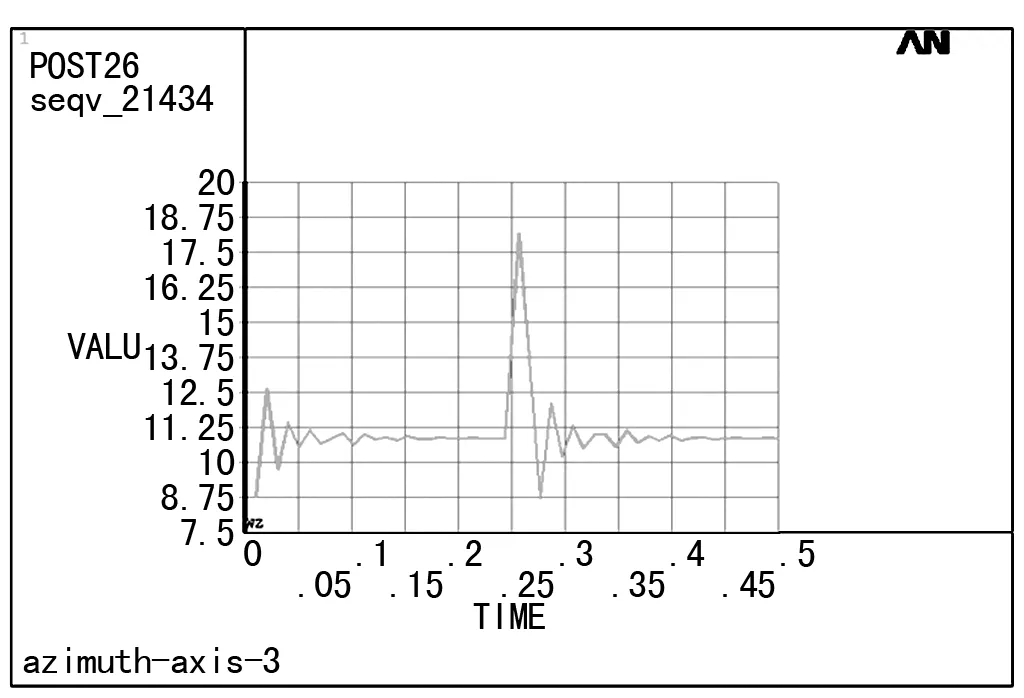
图7 分析点P2的应力随时间变化曲线(x=1.8)
(2) 不同转速下的方位轴瞬态动力学分析结果
文中分析了转速n分别为1和2,冲击载荷系数x为1.4时,方位轴的瞬态响应情况。图8给出了转速n为1时,分析点的应力变化曲线,转速n为2时,分析点的应力变化曲线如图5所示。
从图8可以看出,当方位轴的转速n=1时,各分析点的应力响应曲线中的两个较大峰值出现在了t=0.02 s和t=0.5125 s时刻,即在加载的初始时候和冲击载荷离开的时候,各分析点的应力响应曲线出现了较大的峰值。与图5相比,各分析点的应力最大值均有所增加。从图中也可以看出,当转速n=1时,方位轴各分析点的应力最大值出现在P2处,该值接近16 MPa,未超过材料的许用应力,强度也满足使用要求。


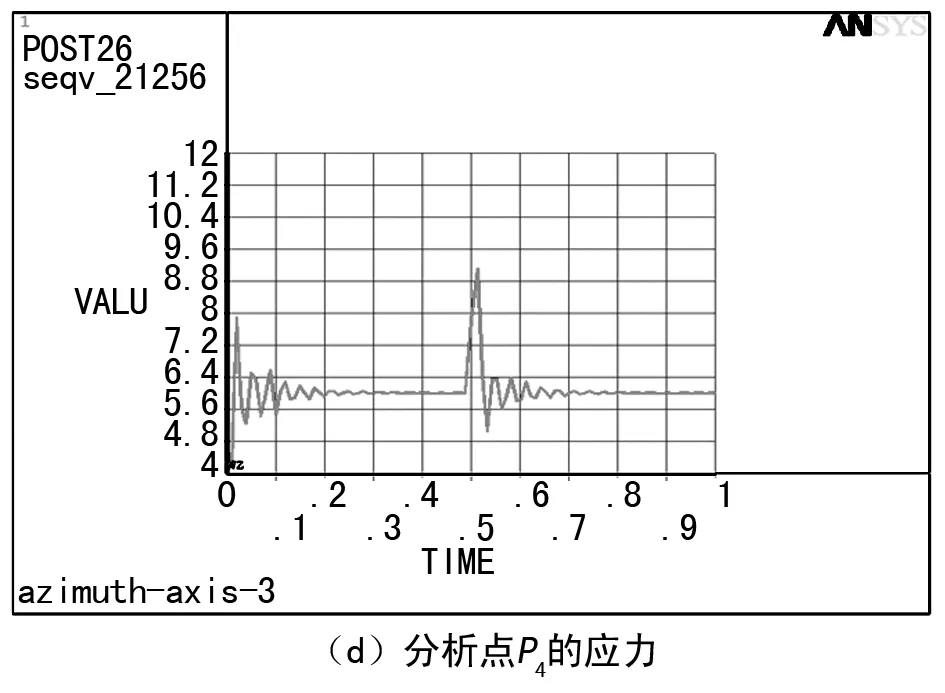
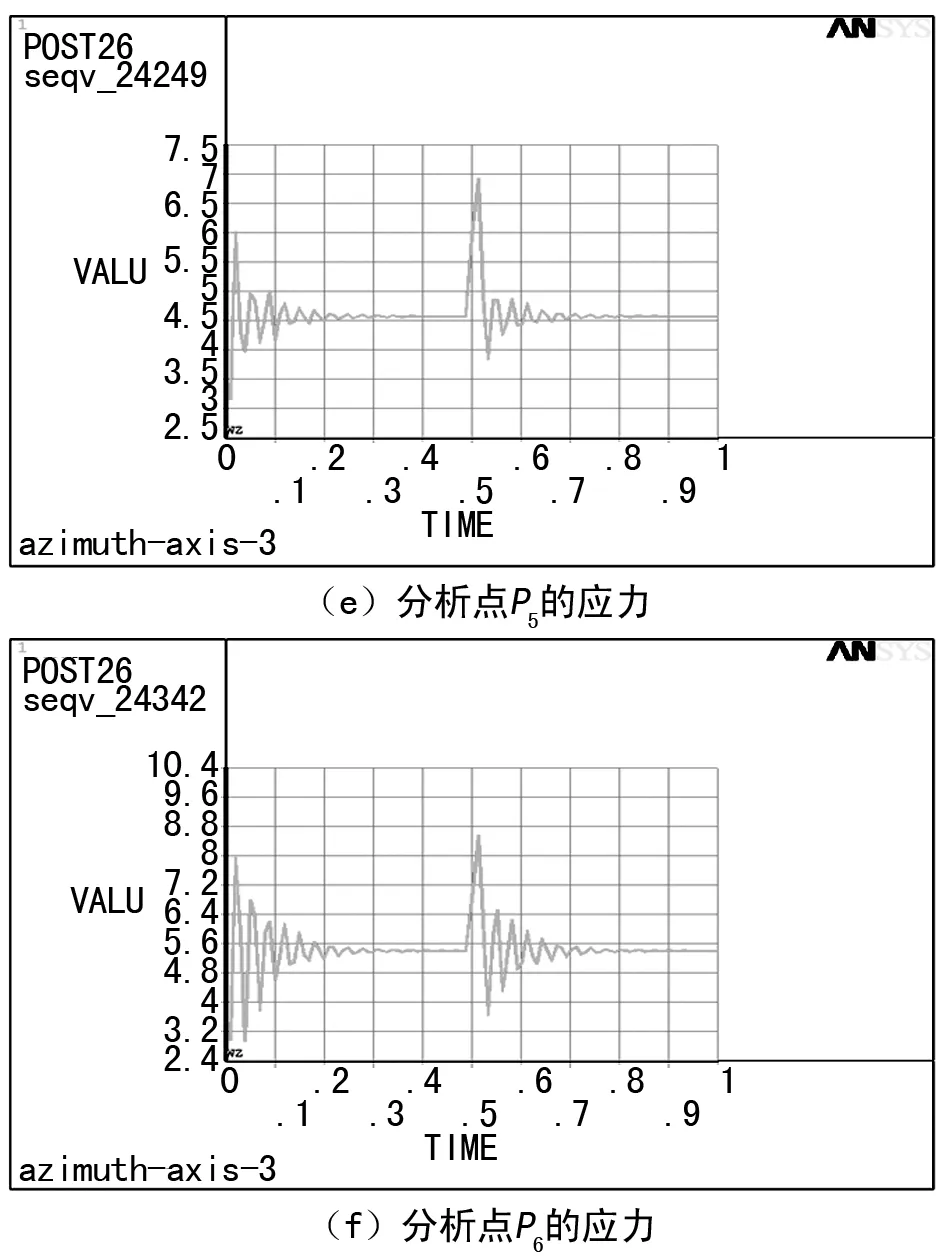
图8 分析点的应力随时间变化曲线(n=1)
3 结 论
利用有限元软件ANSYS对某天线支座方位轴进行了瞬态动力学分析,考察了方位轴在不同冲击载荷大小和转速下的瞬态响应。通过研究得出如下主要结论。
(1) 在瞬态载荷作用下,由于载荷的冲击效应,该方位轴的应力值会随时间发生变化,其较大峰值出现在加载的初始时刻和冲击载荷离开的时刻。
(2) 根据本文分析的载荷和转速工况,随着冲击载荷的增大,方位轴的最大应力值也会增加,当方位轴的转速从2 rad/s降为1 rad/s时,方位轴上各分析点的最大应力值会变大。
