基于马氏距离-数据融合的水电机组运行研究
2021-01-12谭丕成罗正亮张雁靖
谭丕成,罗正亮,潘 虹,张雁靖
(1.湖南五凌电力科技有限公司,湖南 衡阳 421127;2.河海大学 能源与电气学院,江苏 南京 211100)
0 引言
在水电机组运行过程中不乏各种故障的出现,严重影响水力发电安全性、稳定性以及运行效率。以致针对机组运行状态以及运行中所存在故障问题的研究变得十分必要[1]。在前人的研究中,针对水电机组故障诊断的传统方法多依赖于人工经验或提取并分解振动信号,将其作为特征量输入已有数据结构基础上的分类函数或分类模型,进行机组状态识别[2]。但由于传感器数据众多,若未能综合考虑各传感器信号间的相互影响、将多传感器信号进行信息互补和优化组合处理,则无法对机组运行状态提出更为综合、全面、一致性的解释[3~6];加之机组振动信号具有非线性、非平稳性等特征,使得传统的研究方法无法予以较高的时效性以及准确性。
目前,马氏距离因其可衡量样本相似程度这一特性被国内外学者广泛应用于衡量设备运行状态以及模式识别领域的研究中,具有较高故障确诊、排查成功率。如艾延延等[7]应用马氏距离结合EEMD与小波变化完成对轴承振动信号的拆分以实现故障诊断;张红飞等[8]提出通过改进马氏距离,结合滑动窗口对空压机进行状态评估;骆志高等[9]在拉伸件裂纹识别上,引入马氏距离作为评判标准提高工件识别准确率;且越来越多的学者[10~14]将马氏距离应用在轴承等旋转机械上,都成功实现对设备运行状态的评估。
综上,可以发现针对马氏距离在水力机械故障诊断领域中的应用研究少之又少,在目前水电机组存在大量传感器的背景下,若通过数据融合可更好地实现对多传感器数据变化的分析,从而实现对机组运行状态的评估。对此,本文引入马氏距离与多传感器数据融合,利用马氏距离在表征数据样本之间相似程度方面的优异性能,排除多个传感器数据变量之间相关性的干扰[15],并充分发挥数据融合模式所具有的在故障定位上高准确性与可靠性等优点,建立水电机组运行状态综合指标,在保证快速性和高准确性的基础上实现对机组运行状态识别。最后,基于湖南五凌电厂机组实际数据进行实验仿真模拟,验证该方法的有效性与优越性。
1 马氏距离概述
马氏距离是一种无量纲参数,由印度统计学家马哈拉诺比斯所提出,以表示被测数据协方差距离,进而以此度量样本集之间相似程度[16]。样本相似程度反映为距离值大小,成对应比例关系。其定义为:设有两样本x、y,均为含有n个变量的行向量,则x与y对应的马氏距离可表示为[17]:
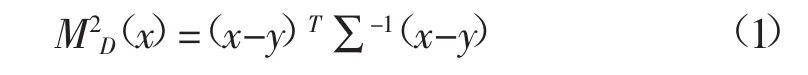
其中,协方差矩阵计算公式为:

作为距离指标,马氏距离具有平移不变性、旋转不变性和仿射不变性[18]等优质特性。其突出特点在于不受数据物理量基本属性影响、将样本中特性关联关系与总体特征集中反映、且建立于以样本总体分布为基础且总体分布一致的特征量上[19]。
2 马氏距离-数据融合机组诊断模型
2.1 数据融合基础理论
传感器数据融合意为将分布在不同位置的多个同类或不同类传感器的数据资源综合,采用计算机技术对其进行分析,消除多传感器信息之间可能存在的冗余和矛盾,加以互补,降低其不确实性,获得被测对象的一致性解释与描述,从而提高系统决策、规划、反应的快速性和正确性,使系统获得更充分的信息。其信息融合在包括数据层融合、特征层融合、决策层融合[20~21]。
多传感器数据融合最终目的是消除单个传感器的局限性,往往单一的传感器在整个传感器系统中无法通过数据变化直观地显示数据背后所代表的结果,需要数据融合以提高整个测量系统的精准度,增强数据的可信度,提高精度,扩展系统的时间、空间覆盖率,增加系统的实时性和信息利用率等[22,23]。因此,多传感器系统往往比单传感器系统更具有优越性和对系统描述的代表性。
具体多传感器数据融合过程步骤包括[24]:
(1)获取信号。从多传感器数据终端接受不同量纲数据,为进行统一管理,需将被测量所具有的不同特征转化为计算机可接受的数字量。
(2)信号预处理。对所取信号采取去噪过程处理,提高被测数据精准度。
(3)特征提取与关联分析。分析并寻找数据中贡献度或潜在贡献度较大特征变量,对其进行关联性分析,实现数据挖掘第一步-数据层融合。将其作为被测对象原始数据用以提取。
(4)信息融合计算。数据挖掘初始化后需进行特征信息融合与决策信息融合,利用计算机程序算法实现数据信息融合后续过程,获得符合预设精度下融合信息结果,若结果不满足要求,则返回至步骤2重新实现信息新一轮预处理-融合过程。
简要融合过程如图1所示。

图1 多传感器数据融合过程
2.2 马氏距离-数据融合模型建立
为构建以马氏距离为基础进行多传感器数据融合的水电机组故障诊断模型,需结合马氏距离与多传感器数据融合的相关理论知识,具体步骤为:
(1)在水电机组模式识别上需采集持续时间内机组不同运行状态时传感器监测数据,
(2)对所采取初始数据进行信号转换、降噪处理以及特征值提取等多传感器数据融合初始步骤。
(3)将提取特征值后具有代表性的数据进行多传感器数据融合,可得到连续时间段内的马氏距离值。
(4)根据距离值变化浮动情况衡量数据彼此相似程度。并结合机组实际运行情况,从而实现对机组运行状态的识别。若出现距离值变化波动大但核实机组并无故障存在的现象,则返回至步骤(2),重新实现对初始数据的预处理。具体流程图2所示。

图2 基于马氏距离的数据融合流程图
3 实验结果与分析
3.1 实验数据与设置
数据来源于湖南五陵水电厂抽水蓄能机组,机组额定功率200MW,发电机型号为SF200-56/11950,立轴半伞式。传感器采集模式为整周期采集模式,保证连续存储周期数是16,每个周期256点,时间分辨率精确到0.1ms。多传感器数据包括机组上导轴承、推力轴承和水导轴承的X、Y方向摆度信号,上机架、顶盖的X、Y、Z方向振动信号,以及蜗壳与尾水管的压力等数据。
数据时间段为2015年8月24日至2015年8月29日。分析基于matlab平台,根据电站历史运行数据与对应工况,建立正常与故障两种运行工况下的训练与测试样本数据库。24日至26日机组运行状态正常无故障出现,27日机组停机无数据,28日机组运行开始出现故障,故障持续至29日数据测量结束。故以28日前后分为正常与故障测试样本,用以验证本文所提方法。
此外,为凸显基于马氏距离-数据融合的方法在数据深度挖掘与表征数据样本相似度上具备的优异性、高效性,设置了基于单传感器与基于欧氏距离-数据融合的机组运行诊断,以达到对比说明的目的。
3.2 基于马氏距离-数据融合的机组运行诊断
为充分具体验证基于马氏距离—数据融合能够在数据反应层面上所具备的有效性与精确性,将8月24日~29日水电机组采集的多传感器数据融合信号保存为十分钟间隔的多组信号,以马氏距离融合连续时间内多传感器数据,结果如图3所示。
观察图3大范围数据波动可分析得:对比28日机组首次开机前后,马氏距离均值从6.1突变至13,增长幅度为113%,且在机组开机后所持续时间段内,马氏距离值并未回归至开机前所维持大致数值,约为开机前数据均值的1.5~2倍,由此次变化可大致确定机组运行状态已发生改变。且根据与电站工作人员所核实,故障发生时间也可确定为8月28日1点10分附近,在当日机组上机架、水车室、蜗壳以及尾水管等处出现异常声音,在之后的开机运行过程中并未消除。结合图3中28日开机后马氏距离值的变化趋势,可见,马氏距离可准确地实现对机组运行状态的识别。
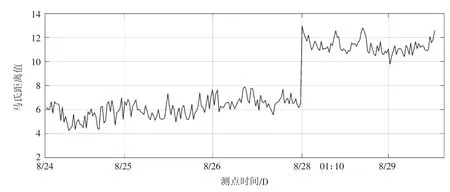
图3 多传感器数据融合马氏距离变化曲线(10min间隔)
为进一步说明图3所反应数值变化表明机组运行状态已然发生改变,且强调变化程度具备足以说明问题的能力,进而验证此次距离值波动并非传感器故障、数据变化异常或实验流程有误所致。对此,从增强实验严谨性与科学性的角度出发,将正常测试样本与训练样本数据库中所存有机组运行数据进行马氏距离计算,如图4所示。线1、线2分别代表测试样本与正常、故障训练样本所得值。
从图4数据变化曲线对比中,所得信息为:两线均值对比明显,线1至线2的增长幅度为95%左右,且数值活动区间较后者大,两者易于区分。根据马氏距离基本概念,距离值越小数据越相似,可知正常训练样本相较于故障训练样本,与正常测试数据更为相似,与机组实际运行情况相吻合。

图4 正常工况下测试样本与训练样本马氏距离
随后将故障测试样本与机组训练样本数据进行马氏距离计算,线1、线2分别代表故障样本与正常、故障训练样本所计算结果。如图5所示。
通过图5数据变化对比,可以发现图5所凸显现象与图4有所相似,即两线对比明显,均值相差程度亦接近于两倍,足以表明相差程度较大。不同之处在于此图表明故障训练样本与故障测试数据更为接近,亦与实际运行情况相吻合。
综上,通过将图4~5测试样本与训练样本进行马氏距离值的对比并结合机组实际运行情况,表明图3马氏距离值的变化并非数据融合过程中存在偶然性、突发性的传感器数据波动或是融合过程不严谨等现象所致,相反,此距离值变化切实反应机组运行状态存在问题,准确地实现了对机组运行状态的识别。

图5 故障工况下测试样本与训练样本马氏距离
3.3 基于单传感器数据分析的机组运行诊断
为验证单一传感器数据分析所具有的局限性,无法完成海量数据的深度挖掘,进行了基于单一传感器的数据分析。样本数据来源于2015年8月24日到8月29日中随机选出的两部分传感器,所测数据分别为上机架X、Y向水平振动,令其数据变化曲线对应为线1、线2,绘制时间-数据变化关系图,如图6所示。
根据图6曲线变化,可看出:①线1振动位移值变化不平稳,数值可观测区间与振动均值波动范围均较线2大;线2数据变化较线1稳定,均值整体在12附近,无大波动。② 28日前后线1观测均值变化区间为21至27,且在测试后期存在较大水平的上升;而线2在28日前后观测均值无明显波动。
进一步分析可知,在故障发生时,只有部分传感器数据会发生变化。如果对应传感器信号变化幅度较小,存在无法及时准确的判断机组运行状态的可能性。表明以单传感器数据为基础进行故障诊断的方法具有不可忽视的局限性,因此,将多个传感器信号进行融合,比较其综合指标在不同运行状态下的数值表征,成为解决该问题的必然选择。
3.4 基于欧氏距离和多传感器数据融合的机组运行诊断
为验证本文所提基于马氏距离数据融合的优越性,进行基于欧氏距离的多传感器数据融合实验,计算水电机组综合运行状态指标,并与基于马氏距离方法的结果进行对比分析。
以8月24日~29日的测试数据为测试样本,10min为间隔,计算连续一段时间内水电机组多传感器融合信号的欧氏距离变化,结果如图7所示。

图6 单传感器数据随时间变化折线图
观察图7可知:① 欧氏距离值起伏次数多,且前后数值变化大。在24日机组初始运行过程中,出现距离值下落后持续一段时间又迅速、短暂的回升情况;在26日机组运行时间段内,存在4次距离值变化较大现象,多为突发性增长,具体表现为数值在增长后开始跌落。②对比28日前后距离值变化情况,再次开机后并未出现迅速的回升情况,机组运行一段时间后,方才出现缓慢上升趋势。③在贯穿数据样本的测试过程中,欧氏距离值并无1~2个稳定的均值,即通过28日前后数据平均水平的对比无法看出明显差异,进而无法由欧氏距离值变化揭示开机前后机组运行状态的区别。
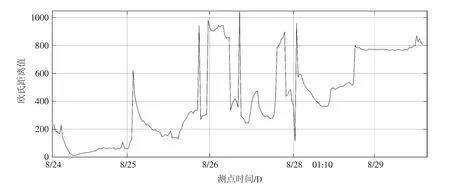
图7 基于欧氏距离和多传感器融合的曲线变化(10分钟间隔)
对比图3与图7不难发现,基于欧氏距离的方法数值无法保持长时间的稳定态势,在电站故障诊断实际应用中,若采用欧氏距离作为多传感器的数据融合,无法精准地判别机组运行状态。而基于马氏距离的方法,数值变化波动次数少,变化小,在数据上不容易产生干扰,更易看出正常样本与故障样本不同之处,能如实反映机组运行状态。
综上所述,结合实验数据与机组实际运行状况,表明基于马氏距离-数据融合的模式识别方法可准确地识别机组的运行状态,提高了机组整体运行状态识别的可靠性与准确性,较单传感器的故障诊断和基于欧氏距离的数据融合,可避免数据精度不高与易产生干扰等问题,具有显著优势。
4 结论
(1)实验结果表明,基于马氏距离-数据融合的方法相较于本文所提其它两种方法,具有低干扰性、高准确性与高可靠性等优异之处,具备数据深度挖掘的能力,能有效、精确地判别机组的运行状态。这一方法对于机组电站运行而言具有重要参考意义。
(2)传感器数据繁多,若结合神经网络或深度学习等方法,能在融合精确性与时效性上有进一步的提高。
