位移载荷在有限元分析中的应用
2021-01-12吴敏
吴 敏
(西南交通大学,四川 成 都 610000)
1 概述
有限元分析是求解复杂微分方程的一种非常有效的数值方法[1],在科学研究和工程分析中广泛运用。它结合计算机技术,具有计算速度快、计算精度高的特点,广泛运用于力学领域、热学领域、电磁学领域以及学科交叉领域中。有限元思想起源于1943年Courant[2]解决St.Venant扭转问题的工作中,Clough[3]在1960年首次提出“有限单元法”的名称。有限元的核心是将一个连续的物体通过离散化的形式来表示,将连续体离散为若干个单元的组合,每个单元通过节点的形式连接。通过离散化的方式将具有无限自由度的物体用有限自由度的离散体近似表示,从而得到相关的数值解。运用有限元对结构的受力情况进行数值仿真时,以节点位移为基本未知量,首先用节点位移来表示离散体单元内部的应力和应变状态,然后通过虚功原理构造单元刚度矩阵,接着将单元刚度矩阵组装成为总体刚度矩阵,并施加边界条件求出每个节点上的位移值,最后将节点上的位移值带入到每个单元中,求解出每个单元的应力和应变状态。
目前关于有限元的文献中,外加载荷的形式普遍采用的是力载荷,几乎没有关于外载荷形式为位移载荷的有限元分析原理的文献,针对这种现象,本文分别推导了外加载荷为位移载荷的形式下有限元原理,并且使用MATLAB 软件分别编写出了外载荷为力载荷和位移载荷的有限元程序。对比两种外载荷形式下的数值仿真结果发现:外载荷为位移载荷计算出的仿真结果与外载荷为力载荷计算出的仿真结果基本一致。由此可以拓展有限元的分析思路:当外加力载荷不容易确定时,通过测量位移载荷的大小来对结构进行有限元分析,同样可以得到结构的有限元受力结果。

图1 结构的有限元受力分析步骤
2 有限元分析步骤
在对结构的受力情况进行有限元分析时,以节点位移为基本未知量,主要分析步骤采用的是“总-分-总-分”的形式[4],即首先将结构离散化为若干个单元,然后再求出单元刚度矩阵,接着将若干个单元刚度矩阵组装为一个整体刚度矩阵,并且施加边界约束和外加载荷,求出节点位移,最后将求出的节点位移带入到每一个单元中,求解出每一个单元的应变和应力情况。有限元受力分析的流程图如图1 所示。在本文中,以一个二维平面的连续体为例,来推导有限元的分析步骤[5]。其中,单元类型采用的是的目前广泛使用的三节点三角形单元,如图2 所示。

图2 三节点三角形单元
2.1 结构离散化
将一个二维的连续体离散为具有若干个三节点三角形单元,通过离散化处理,将具有无限自由度的连续体近似等效为有限自由度的离散体。图3(a)和(b)分别表示一个二维的连续体和三节点三角形单元表示的离散体。

图3 二维平面的连续体和离散体对应的结构示意图
2.2 单元分析
将结构经过离散化处理后,结构由若干个离散的单元表示。在单元分析的过程中,将用单元的节点位移分别表示单元内部位移、单元应变和单元应力,并且求出单元刚度矩阵。
2.2.1 单元内部位移
在每一个单元中,引入形函数,则单元内部任意一点的位移可以通过单元上的节点位移来表示。

式(1)中,ue=[uiviujvjukvk]T表示单元的节点位移,a=[uv]T表示单元内部任意一点的位移,N 表示形函数矩阵,表达形式为:

式(2)中,Ni、Nj、Nk是与节点坐标和位移待求点坐标有关的函数,称为形函数。在这里,形函数采用一次多项式的形式,表达形式为:
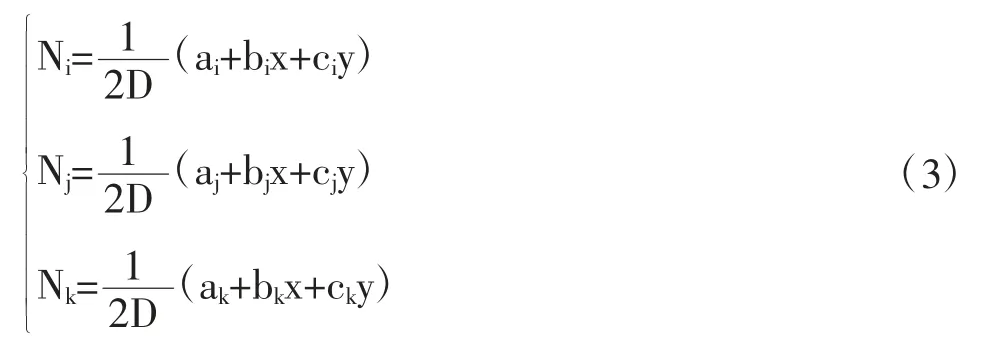
式(3)中,D 代表三角形单元的面积,x、y 表示单元任意一点的坐标,其他系数的表示形式为:

式(4)中,“(i,j,k)”的意思是依次将下标做轮换:i→j,j→k,k→i。这样,所有的待定参数都可以通过节点位置来表示。
2.2.2 单元应变
在确定了单元内任意一点的位移之后,通过几何方程即可确定单元内的应变:
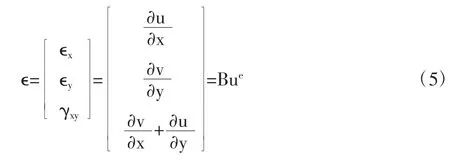
式(5)中,∈为单元应变矩阵,B 为形函数导数矩。在三节点三角形单元中,B 的表示形式为:

2.2.3 单元应力
求出单元应变以后,利用物理方程可以求出单元内的应力分布:

在二维平面情况下,结构可以分为平面应力问题和平面应变问题。对于平面应力问题,D 可以表示为:

对于平面应变问题,D 可以表示为:

式(8)和式(9)中,E 为弹性模量,μ 为剪切模量。
2.2.4 求解单元刚度矩阵
在求出应变和应力的表达方式以后,通过虚位移原理可以得到单元刚度矩阵和单元节点力列阵。虚位移原理可以表示为:
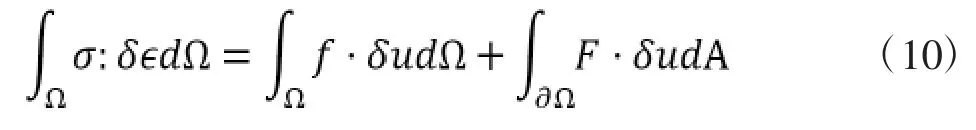
式(10)中,f 和F 分别表示体积力和面积力。在离散化结构中,单元内的虚位移原理可以表示为:
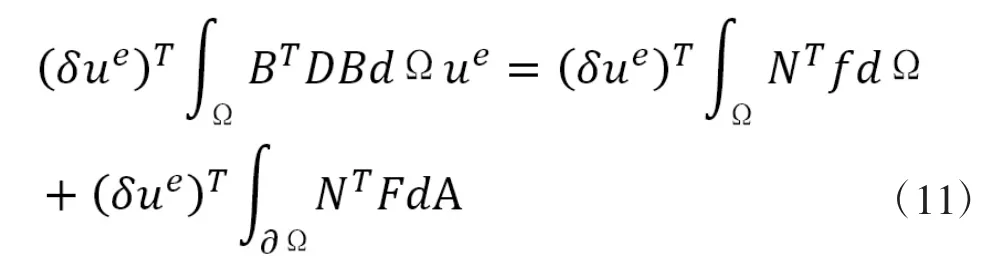
经过化简后,可以得到单元内部的有限元方程:

2.3 整体分析
在整体分析的过程中,首先将单元刚度矩阵组装成整体刚度矩阵,然后施加边界条件和外加载荷,最后计算求解出节点位移。
2.3.1 求解整体刚度矩阵
在求出单元刚度矩阵和单元节点力列阵后,将若干个单元的单元刚度矩阵和节点力列阵进行组装,即:

式(13)就是结构受力分析的有限元方程,将其简化书写为:

式(14)中,K 为整体刚度矩阵,u 为整体位移列阵,P为整体节点力列阵。将有限元方程展开为矩阵形式,可以写为:

2.3.2 施加边界条件和外载荷
边界条件通常是限制结构在某些位置上的位移,表达形式为:

外载荷的加载形式有位移加载和力加载两种形式。两种施加方式的求解过程有所不同,下面分别推导外载荷形式为力载荷和位移载荷下的有限元方程的求解过程。
(1)外载荷形式为力加载的有限元求解过程
当外载荷形式为力载荷时,力载荷的加载形式可以表示为:

将边界条件和力载荷加入到整体分析的有限元方程中并用矩阵形式表示,可以得到:

式(18)中,u1和 P2是已知的参数,u2和 u3为待求的节点位移值。此时,可以将有限元方程简化为:

由式(19)即可求得待求的节点位移u2和u3。
(2)外载荷形式为位移载荷的有限元求解过程
当外载荷形式为位移载荷时,位移载荷的加载形式可以表示为:

将边界条件和位移载荷加入到整体分析的有限元方程中并用矩阵形式表示,可以得到:
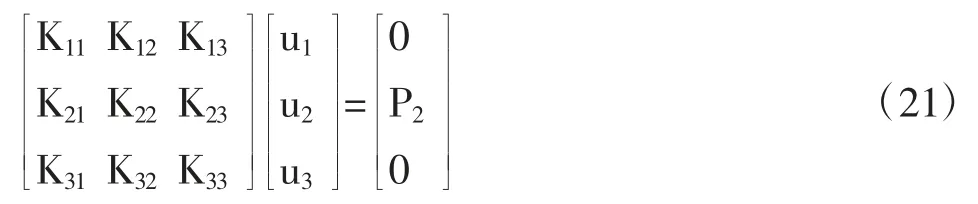
式(21)中,u1和 u2是已知的参数,u3和 P2分别为待求的节点位移值和节点载荷值。此时,可以将有限元方程简化为:

由式(22)即可求得待求的节点位移u3,然后将求出的节点位移值带入到式(21)中即可求得力载荷P2。
2.4 离散体的受力分析
在求出离散体的节点位移以后,首先通过式(5)求解出每个单元的应变分布,然后通过式(7)求解出每个单元的应力分布。
3 数值仿真实例
在数值算例中,我们运用MATLAB 软件编写出力载荷和位移载荷下的有限元程序,在MATLAB 软件中完成了力载荷和位移载荷下的有限元仿真,并且得到相关的数值结果。
3.1 外载荷形式为力加载的数值实例
如图4 所示为二维平面的矩形板。矩形板的长为3m,宽为 1m,弹性模量为 E=1×107Pa,泊松比 μ=0.3,在矩形板右上方的顶点处施加的力载荷大小为F=1×105N。使用三节点三角形单元,并采用平面应力假设,求解矩形板每个节点上的位移。

图4 力载荷作用下的矩形板及其有限元几何模型
受力载荷作用下的有限元分析步骤如下所示:
(1)将矩形板进行离散化处理;
(2)使用式(12)求解出每一个单元的单元刚度矩阵;
(3)使用式(13)组装整体刚度矩阵;
(4)处理边界条件和力载荷
矩形板的边界条件为:
u7=v7=u8=v8=0;
外加的节点力载荷为:
Py1=-1×104N;
(5)求解未知的节点位移
运用式(18)和式(19),求出节点位移列阵为:
u=[0.0069-0.0329-0.0058-0.0315 0.0057-0.018-0.0052-0.0174 0.0035-0.0064-0.0034-0.0059 0 0 0 0]T;
(6)求解单元内的应力状态
将节点位移带入到每一个单元内,可求出力载荷情况下单元1~6 中的应力状态,具体数值如表1 所示。
3.2 外载荷形式为位移加载的数值实例
如图5 所示为一个二维平面的方形板。矩形板的长为3m,宽为 1m,弹性模量为 E=1×107Pa,泊松比 μ=0.3,在矩形板右上方的顶点处施加的位移载荷大小为u=-0.0329m。使用三节点三角形单元,并采用平面应力假设,求解矩形板每个节点上的位移和每个单元的应力值。
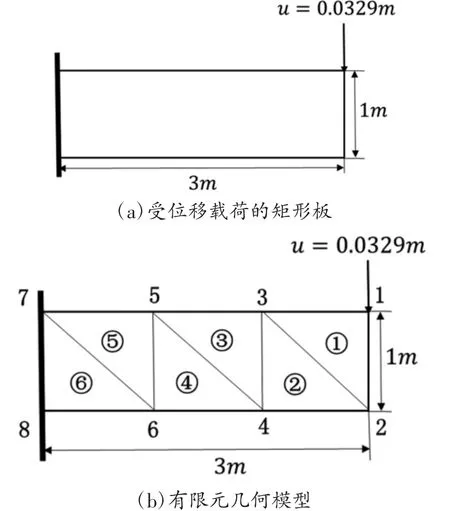
图5 位移载荷作用下的矩形板及其有限元几何模型
受位移载荷作用下的有限元分析步骤如下所示:
(1)将矩形板进行离散化处理;
(2)使用式(12)求解出每一个单元的单元刚度矩阵;
(3)使用式(13)组装整体刚度矩阵;

表1 力载荷下各单元的应力值(Pa)

表2 位移载荷下各单元的应力值(Pa)
(4)处理边界条件和位移载荷
矩形板的边界条件为:
u7=v7=u8=v8=0;
外加的节点位移载荷为:
v1=-0.0329m;
(5)求解未知的节点位移和外加力载荷
使用式(21)和式(22)求解未知的位移,求出的节点位移列阵为:
u=[0.0069-0.0329-0.0058-0.0315 0.0057-0.018-0.0052-0.0174 0.0035-0.0064-0.0034-0.0059 0 0 0 0]T;
使用式(21),求得施加位移载荷时等效的外加载荷,其值为:
Py1=-0.993×103N;
(6)求解各单元的应力情况
将节点位移带入到每一个单元内,可求出位移载荷情况下单元1~6 中的应力状态,具体数值如表2 所示。
3.3 两种外加载荷的仿真结果比较
使用力载荷加载计算出的位移结果和使用位移载荷计算出的位移结果几乎一致,两种外加载荷计算出来的应力结果也大致相同。说明使用两种不同的外加载荷进行有限元分析得到的数值结果是一致的,验证了运用位移载荷进行有限元分析的正确性。
4 结论
本文分析了外加载荷分别为力载荷和位移载荷情况下的有限元原理,并且使用MATLAB 软件编写了两种外加载荷在二维平面应力问题下的有限元程序,验证了运用力载荷和位移载荷对结构进行有限元分析时仿真结果的一致性。为结构的有限元分析扩展了思路。当结构的外加力载荷不容易得到时,通过测量位移载荷的大小也可以对结构进行有限元分析。
