基于智能体联盟的多配送中心路径优化研究

（安徽理工大学 经济与管理学院，安徽 淮南 232001）

电子商务的快速发展将物流推向风口浪尖，各界学者和企业管理者将研究目光转向物流领域，各物流公司在降低物流成本、提高客户满意度等方面竞争也愈加激烈。随着市场需求日益增长，单配送中心配送压力大，易导致车辆调度失衡、物流成本增加、配送效率降低，已不能适应企业发展。而多个配送中心进行进行配送时，需要各配送中心根据配送地点、需求数量、需求种类来合理规划路线，这就需要配送中心实现信息实时共享，协作配送，实现配送规模化，从而提高配送车辆利用率、降低配送成本。

在车辆配送中，秦敏[1]、毕国通[2]等学者只研究了单配送中心车辆配送，然而单个配送中心切断区域间的联系，使得物流资源难以共享，导致车辆配送成本增加。经济的快速发展使得客户对粮食[3]、冷链食品[4]的需求增多，单配送中心显然已不能满足客户对期望配送时间的要求。在多配送中心车辆路径研究上，高珊珊[5]提出时间窗概念，引入惩罚因子，在满足配送成本的同时，提高客户满意度。苏海倩[6]在此基础上考虑碳排放量，为绿色物流打下基础。日本最早提出协同配送，要求有组织任务的各配送中心形成联盟，共同组织配送任务，Andrsm[7]采用哥伦比亚首都圣菲波哥大的真实数据来比较联盟与未联盟的差异，事实证明，配送中心形成联盟卓有成效。张占云[8]结合人工智能，在协同配送基础上，提出了基于智能体交互的联盟，各配送中心和客户点能够根据具体环境协调、合作求出适应环境的最优解。求解多配送中心车辆配送模型时，Yong Wang[9]提出包含k-means、NSGA-II的混合算法，将客户大致分类，转化为多个单配送中心配送问题，虽简化了算法，但求解出来的配送路线并非最优，还会出现资源浪费现象(如车辆空载率高、人员配备冗余)和客户满意度降低。侯宇超[10]提出精英蚁群算法，来避免传统蚁群算法陷入局部最优和增大算法收敛性。

1 问题描述

1.1 多配送中心车辆路径问题描述

多配送中心车辆路径问题是研究车辆从多个配送中心出发向多个客户点服务的过程。一般可以描述为在整个物流系统中有多个配送中心，车辆从各自所在的配送中心出发，选择合理的配送路线对客户进行物流服务，使其在满足客户需求，配送车辆满足时间窗要求、车辆容量、行驶里程和配送时间约束条件下，达到整体目标最优(如配送成本最低、车辆行驶路径最短、服务时间最短、车辆空载率低等)。

1.2 智能体联盟问题描述

智能体是在某个特定的环境下，与外界环境交互，自发解决特定任务的计算机系统，具有自主性、分布性、协调性等特点。多智能体系统中，每个智能体负责系统中某一模块，具有相当独立性，通过协调、沟通、合作完成系统整体任务。智能体之间结构是动态的，可以依据具体环境进行调整，具有一定的适应性。基于智能体的联盟的多配送中心核心思想是将模型中单个配送中心和客户点看作一个智能体，从而将多配送中心车辆路径问题转化为多任务环境下的智能体联盟问题，求解智能体间如何联盟合作使整体效果最优。在车辆配送时，各配送中心和客户点自主协调、合作找出满足条件最优解。

各个智能体之间通过黑板模式进行协调沟通，从而形成联盟。黑板是各智能体进行交流沟通的公共区域，每个智能体从黑板中发生和获取信息，从而完成系统赋予自己的任务。多配送中心智能体联盟配送可以描述为：首先客户对产品需求形成订单，订单智能体将客户需求传送给各配送中心，配送中心智能体实时接收车辆智能体和仓库智能体发送信息，各配送中心智能体之间根据订单智能体需求，通过黑板协调沟通，合理安排车辆和货物，形成动态联盟。多配送中心智能体联盟配送如图1。

智能体联盟问题可以描述为：设有n个智能体的集合N={A1,A2,…,An},现有任务集T={t1,t2,…tm}需要并行执行，其中任务tj最低的能力需要为。联盟C为N的一个非空子集，问题的一个合法解定义为：寻找N的一个联盟结构Cs={C1,C2,…Cm}，要求对于任意的i,j＜m,i≠j,Ci∩Cj=φ,任意i≤m,Ci中所有智能体能力总和满足任务tj的能力需求。联盟Ci的成本特征函数为V(Ci)=F(Ci)+G(Ci)，D(Ci)≤Di,i≤m。式中：F(Ci)为联盟Ci的成本；G(Ci)为联盟Ci的通信或合作开销。

2 MDVRP 模型建立

2.1 模型假设

为了便于建立MDVRP 模型，使该模型简洁又具有一定的实用性，假设系统满足以下条件：

(1)配送中心，客户点的地理位置、需求量已知；(2)运输对像为同种类型，满足运输规范；(3)配送中心库存充足，产品种类和数量满足客户需求；(4)每个客户的需求量不得超过车辆容载量，车辆出发到返回配送中心行驶的总距离不得超过车辆的最大行驶距离；(5)每个客户点只能由一辆车进行服务，且车辆最终需返回配送中心。

2.2 基于软时间窗的MDVRP

配送时，客户往往要求在规定的时间内送达，这就提出了车辆路径时间窗的概念。在实际过程中，由于一些不确定因素，配送时间未在客户期望的时间段内到达客户手中，但客户也存在可接受的上下界时间窗，若在客户可接受的时间窗内送达，则只需付出一定的惩罚费用，不影响配送结果。若配送时间超出客户可接受范围，则客户拒绝接受货物，设惩罚费用无穷大。问题描述为：ETi为客户i期望最早服务时间，LTi为客户i 期望最迟服务时间。在[ETi,LTi]时间窗内，客户乐意接受货物，满意度为100%。EETi为客户i可接受的最早服务时间，LLTi为客户i可接受的最迟服务时间。在时间窗[EETi,ETi]和[LTi,LLTi]内，客户可接受服务，但需付出一定的惩罚费用。若服务时间早于EETi或晚于LLTi,客户i拒绝接受货物，惩罚费用无穷大。客户软时间窗下满意度如图2。

惩罚成本为：

其中：Pt为有时间窗约束的惩罚成本，∂为在时间窗[EET,ET]内服务客户的惩罚系数，b为在时间窗[LT,LLT]内服务客户的惩罚系数。

2.3 参数定义

I={i=1,2,…n}表示客户订单集合；M={m=1,2,…m0}表示配送中心集合；L={l=1,2,…I0}表示配送车辆集合；dij表示客户点i到客户点j的距离；Fl表示第l辆车的固定成本；ti表示到达客户点i的时间；Cd表示单位距离内产生的运输成本；Dl表示车辆l行驶的最大距离；Ql表示车辆l的最大载重量；qi表示客户i的需求量。

(1)车辆固定成本：车辆固定成本包括车辆的购买费、燃油费、修理费、定期保养费以及支付给司机的人工费。车辆的固定成本与执行任务的车辆数量有关，与道路状况和行驶过程无关。车辆固定费用用S1m表示从配送中心m出发nm车辆的总固定成本。

(2)车辆运输费用：车辆运输费用是指车辆l从配送中心m出发，向客户i进行配送，再转向客户j,最终回到配送中心m产生的运输费用。车辆运输成本与距离成正比例关系，用S2m表示。

(3)车辆惩罚成本：根据上述对软时间窗下车辆配送的探讨，车辆惩罚成本用S3m表示。前半部分是对早于最早期望ET的机会成本，后半部分是晚于最迟期望时间LT的延迟成本。

2.4 模型建立

根据上述对目标函数分析，模型建立为：

其中：式（4）表示为各配送总成本之和最低的目标函数；式（5）表示分配给车辆l的总订单路程不得超过车辆l的最大行驶距离；式（6）表示分配给车辆l的总订单需求量不得超过车辆l的容载量；式（7）表示每个客户i只能由一辆车进行提供一次服务；式（8）表示执行任务的车辆l从配送中心出发，最终返回配送中心。

3 改进蚁群算法求解MDVRP 问题

3.1 处理方法及分析

多配送中心车辆路径问题本身就是一个non-deterministic polynomial problems（NP）问题，随着客户点的增加，可选方案求解数量会急剧增加，这对求解问题最优解带来了困难。

改进蚁群算法是采用正反馈机制的模拟进化算法，具有较强的鲁棒性，且易于结合其他算法的优点。因此，改进蚁群算法适用于MDVRP 问题。在用改进蚁群算法求解MDVRP 问题时，将配送中心和客户点看作智能体，一群人工蚂蚁根据信息素和启发信息在配送中心和客户点行走，更新禁忌表，直至所有蚂蚁都完成搜索，获得联盟最优解。

3.2 改进蚁群算法

蚁群算法虽在求解性能上，具有很好的鲁棒性和搜索能力，但当客户点较多时，蚁群算法搜索时间过长且收敛速度慢，易陷入局部最优。因此，为了让蚁群算法适用于多配送中心车辆配送问题，通过首先使用轮盘赌法随机选择初始值，在生成初始解后，对其实施交叉，翻转操作，增加种群多样性，从而提高解的质量。在完成一次循环后，对选定的蚂蚁遍历路径进行信息的添加，来改进信息素，加速收敛。更新信息素时加入最优路径额外的信息素量，使得最优解得到更多的利用。找到全局最优解的蚂蚁成为“精英蚂蚁”。

对信息素总量Q实行三段函数进行优化，规则如下：

其中：iter为当前迭代值，iter1、iter2、iter3为设定的一定临界值。

改进的蚁群算法基本步骤：

Step1：设置初始化参数，首先对算法中所有参数进行初始化处理。

Step2：构建解空间，轮盘赌法为蚂蚁随机选择出发点，按状态转移规则选择下一个代访问的客户点，选择之后更新禁忌表。

Step3：对客户点进行交叉、翻转、插入操作，更新禁忌表，所有蚂蚁完成一次循环后构成一个路径解。

Step4：更新信息素，按照信息素更新规则更新信息素。

Step5：最优路径添加额外信息素，找到精英蚂蚁。

Step6：判断是否达到最大迭代次数，若达到最大迭代次数，则进行下一步；若未达到最大迭代次数，则当前次数加1 并清空禁忌表，返回Step2。

Step7：输出最优解，若蚂蚁循环达到最大迭代次数，则完成迭代输出最优解。

4 实例验证

4.1 数据采集

本文选取4 家配送中心和30 个客户点为研究对象进行分析，依托matlab2015b 进行算法编程，求解车辆配送最优解。4 家配送中心和30 个客户点的地理位置、客户需求量及期望时间如表1、表2所示。

表1 配送中心位置

表2 客户资料表

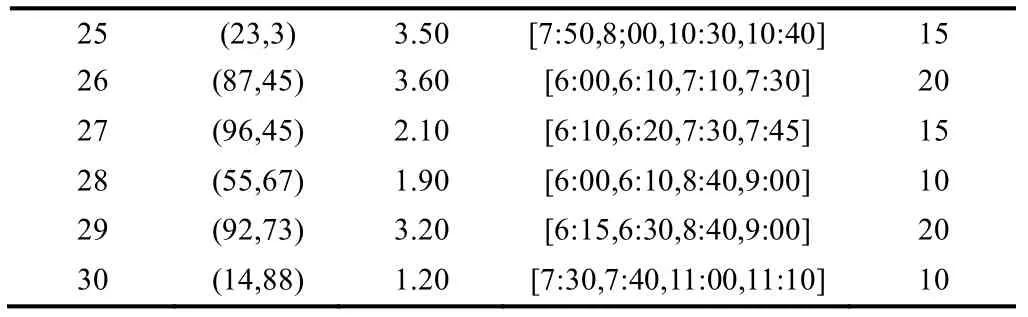
4.2 参数设置

通过多次试验和参考相关文献，现设蚁群算法中最大迭代次数Maxlt=300；蚂蚁数量nAnt=20;信息素更新参数Q=50；初始信息素tau0=8；信息素最小值tau_min=1.2；信息素权重α=2；启发因子权重β=3；信息挥发系数ρ=0.05。

设模型第l 辆车固定成本Fl=200；单位距离内产生的运输成本Cd=5；车辆l 行驶的最大距离为200 km；车辆l 的最大载重量为15 t，车辆速度为40 km/h。

4.3 算法分析

运用改进蚁群算法求得最佳路径为配1-24-6-28-9-配 1；配 2-5-3-30-20-配 2；配2-1-7-23-22-配 2；配 2-16-10-25-21-配 2；配3-29-19-8-12-配 3；配 3-26-2-27-17-配 3；配3-14-15-18-13-配3；配4-4-11-配4。改进蚁群算法求解车辆配送路径图见图3

而蚁群算法求得的最佳路径为配1-29-28-1-30-9-配1；配2-5-3-20-21-25-16-配2；配3-23-7-13-配3；配3-2-27-14-17-10-22-配3；配3-26-12-15-18-配3；配4-4-11-6-24-19-8-配4。蚁群算法求解车辆配送路径图见图4。

从表3 可以看出改进蚁群算法在求解总距离和总成本上都优于蚁群算法，额外信息素避免了结果陷入局部最优。

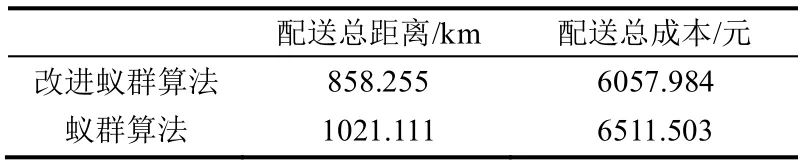
表3 配送距离与成本

由仿真收敛图可以看出，改进蚁群算法(如图5)在不到20 代急剧收敛，在50 代已经趋于平稳，而蚁群算法(如图6)在100 代才趋于平稳。改进后的蚁群算法在速度和质量上都有明显提高。

实验结果表明，本文改进蚁群算法求得的解在总距离和总成本上都优于蚁群算法求得的解。虽然改进蚁群算法在算法上较为复杂，但通过交叉、翻转操作，增加种群多样性，从而增加可行路径解数量，在更新信息素时加入最优路径额外的信息素量，指定精英蚂蚁，在精英蚂蚁的带领下，避免陷入局部最优，快速找到最优路径，增加了算法的收敛性和蚁群的寻优能力。

4.4 未联盟配送中心对比

在以未联盟配送中心计算案例时，先用k-means 聚类分析将各客户点到配送中心距离远近划分给各配送中心，依托R 软件3.6.1 进行算法编程，编程结果如图7。

经过k-means 分类，将问题转化为多个单配送中心求解，用改进蚁群算法，依托matlab2015b 求得各单配送中心车辆配送路径，配送路线、单配送中心距离及成本如表4。

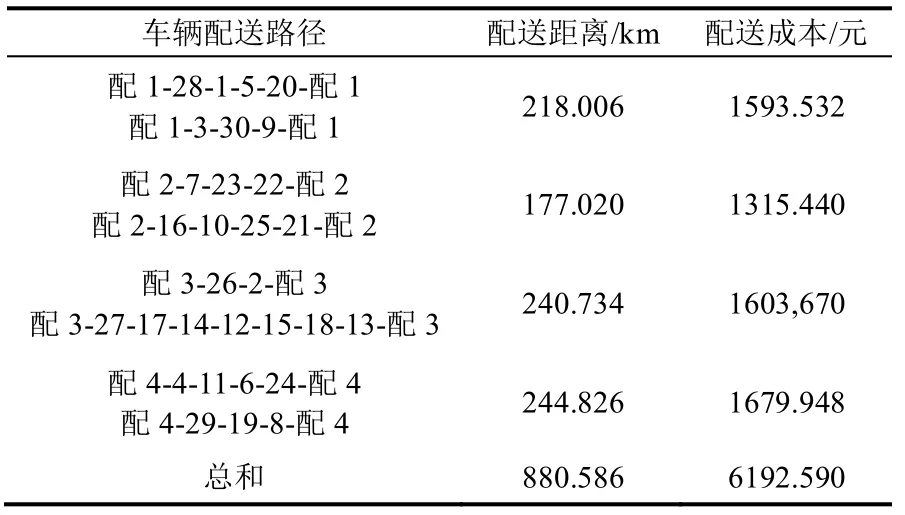
表4 单配送中心车辆配送

由表3 与表4 可知，多配送中心联盟的配送总距离为858.255 km，总成本为6 057.984 元，而独立存在的多个配送中心配送总距离为880.586 km，总成本为6192.590 元。在表4 中，向有的客户进行配送服务时，车辆负载率很低，这时就需要各配送中心之间通过黑板模式将客户信息共享，通过沟通，协调，合理安排车辆路线，提高配送车辆的资源利用率，降低配送成本。

5 结论

在物流配送过程中，车辆路径问题是重要环节之一，路径规划合理与否直接影响着整个配送过程的效率。在现实生活中，配送中心往往由于缺乏信任、信息更新不及时而忽视了联盟带来的成本降低、资源利用率高等优势。本文通过对比配送中心联盟与配送中心未联盟，得出配送中心联盟的配送距离和配送成本明显更优。企业为了更好的运营，联盟是大势所趋。在求解多配送中心车辆配送模型时，改进蚁群算法在解的求解速度和质量上明显优于传统蚁群算法。本文建立的模型是在理想假设的情况下，与实际配送存在差距，需要我们将更多的现实条件加入约束条件，使得车辆配送更加具有现实性。