不可压缩Ericksen-Leslie液晶模型局部适定性的研究

牛 聪,孙建筑,唐 童

(1.河海大学理学院,江苏 南京 210098)(2.南京林业大学应用数学系,江苏 南京 210037)

日常生活中,我们最常见的物质状态是固态、液态和气态. 从结构组成来说,这些状态都是由分子或原子的集合形式所决定的. 由于分子或原子在这3种物态中运动状况不同,从而使我们看到了不同的特征. 而液晶,是介于液态与结晶态之间的一种物质状态,是一种在一定温度范围内呈现出既不同于固态和液态,又不同于气态的特殊物质状态. 从宏观上说,液晶既表现出晶体的典型特征――光学双折射性,又表现出流体的特征――流动性. 从微观上说,在这种特殊物质状态下,材料像流体一样流动,但其分子保持着晶体分子的有向结构特性. 液晶在物理、化学、材料学等众多学科中都取得了重大的研究成果,具有广泛的应用背景. 因此,物理学家和数学家先后建立了各种数学模型来研究液晶,其中最著名的模型是Ericksen-Leslie模型,它是用来描述向列型液晶流体动力学理论的模型,并成功应用于各个领域.

液晶的流体动力学理论是在20世纪60年代由Ericksen[1-3]和Leslie[4]建立的. 液晶分子是比较复杂的分子,为了更好地研究液晶的物理性质和物理现象,我们常常把向列型液晶分子理想化地假设成首尾对称的长棒状,并且沿长轴是旋转对称的. 这种液晶分子称为单轴液晶分子,其质心的位置和长轴的指向确定了单轴液晶分子的构型. 向列型液晶的粘度小,流动性强. 产生这种流动性的原因主要是由于各个分子容易顺着长轴方向自由移动. 在这篇文章中,我们在区域T3×(0,∞)上考虑了如下的抛物双曲系统[1-5]:

divu=0,

(1)

∂tρ+div(ρu)=0,

(2)

(3)

(4)

(ρ,ρu,d,∂td)(·,0)=(ρ0,ρ0u0,d0,d1)(·),d0·d1=0 inT3.

(5)

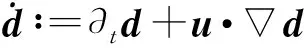
(6)

另外,受到Navier-Stokes方程的启发,我们将假设以下的相容性条件:

(7)

方程(1)—(3)是我们熟知的Navier-Stokes方程. 特别地,当u=0时,方程(4)简化为波动映射方程,方程(1)—(5)是Ericksen-Leslie模型的简化版本. 无论是完整的Ericksen-Leslie模型,还是简化版的Ericksen-Leslie模型,在流体速度u和向列型液晶的微观取向构型d的影响下,这两个模型都是从连续介质力学出发得到的宏观模型. 虽然上述模型是Ericksen-Leslie模型的简化版本,但它仍然具有重要的数学研究价值.

和流体类似,液晶方程分为可压缩和不可压缩两种类型,下面我们分别介绍一下相关工作.

文献[5]研究了简化的Ericksen-Leslie模型在区域Ω⊂R3内的可压缩向列型液晶的强解,并且当初值ρ0,u0,d0充分正则并满足相容性条件时,证明了一个唯一强解的局部存在性. 文献[6]研究了在RN(N=2,3)中具有周期边界条件的可压缩液晶流体的不可压缩极限;然后利用不可压缩极限,严格证明了具有小初值的不可压缩系统强解的局部存在性和全局存在性;此外,在一定意义上得到了收敛速度. 文献[7]考虑了三维可压缩向列型液晶材料的简化流体动力学模型的短时间强解;并利用速度梯度变形张量的最大范数和液晶方向场梯度的最大范数的平方关于时间的积分,建立了在有限时间内这些解可能爆破的准则. 文献[8]研究了当初值满足相容性条件时,证明了在一个有界区域Ω⊂R3内向列型液晶的可压缩非等熵模型强解的局部适定性. 文献[9]研究了Ericksen-Leslie液晶动力学方程组适定性问题,并在第三章研究了可压缩液晶动力学方程组适定性方面的问题.

至于不可压缩方面,文献[10]证明了问题(1)—(5)强解的局部适定性,其中infρ0>0;并且文献[11]和文献[12]分别证明了具有真空但没有任何相容性条件的不可压缩液晶模型的一个新的正则性准则与初始密度为正时的三维不可压缩液晶模型的一个新的正则性准则. 文献[13]研究了N维(N=2,3)不可压缩向列型液晶流体的流动,并且当初始密度ρ0≥0,得到了解的局部存在性和唯一性;特别地,当ρ0有正的下界并且在二维情况下,得到了带有小初值的解的全局存在性和唯一性. 文献[14]研究了不可压缩Ericksen-Leslie双曲模型,在保证基本能量定律耗散的Leslie系数约束下,证明了具有有限初始能量系统的经典解的局部存在性和唯一性;在此基础上,通过对阻尼系数和初始能量极小性的附加假设,建立了唯一的全局经典解. 文献[9]研究了Ericksen-Leslie液晶动力学方程组适定性问题,并在第五章利用非Ginzburg-Landau逼近不可压缩液晶方程,证明了二维不可压缩液晶动力学方程组存在整体强解. 文献[15]从微观Doi-Onsager理论出发,给出了宏观Ericksen-Leslie理论的一个严格推导,在第二章,证明了Ericksen-Leslie方程的局部适定性以及小初值解的整体适定性.

本文目的是在真空情形下证明问题(1)—(5)在相容性条件(7)下的强解具有局部适定性.

本文的主要结果如下:

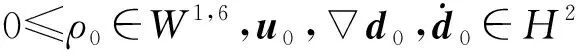
(8)

对某些0

由于强解存在性的证明可以用经典的Galerkin方法得到[16],唯一性的证明由(8)的正则性得到,所以我们只需要给出先验估计(8). 为此,我们定义:

(9)

定理2对任意的t∈[0,T],我们有

(10)

从式(10)和文献[17-19]可知:

M(t)≤C.

(11)

根据Kato-Ponce在文献[20]中的方法,在接下来的证明中,我们将使用双线性交换子和先验估计:

‖Ds(fg)-fDsg‖Lp≤C(‖f‖Lp1‖Ds-1g‖Lq1+‖g‖Lp2‖Dsf‖Lq2),

(12)

‖Ds(fg)‖Lp≤C(‖f‖Lp1‖Dsg‖Lq1+‖Dsf‖Lp2‖g‖Lq2),

(13)

因此,我们只需要证明定理2.

1 定理2的证明

证明首先,由极大值原理及(1)—(2)知:

0≤ρ≤C0.

(14)

利用Gagliardo-Nirenberg不等式:

我们得到:

(15)

因此,由Gronwall不等式知:

(16)

很容易证明:

(17)

在(3)两端用∂t作用,并乘ut,利用(1)和(2),我们推出:

(18)

下面我们证明Ii(i=1,…,4)的有界性:

|I2|≤‖ρt‖L2‖u‖L6‖u‖L6‖ut‖L6≤C(M)‖ut‖L6≤

‖(u·d)‖L2)‖ut‖L2≤C(M)‖ut‖L2.

这里我们利用了Poincaré不等式:

(19)

将上述估计插入(18)得到:

(20)

因此,我们有:

(21)

因此,我们有:

(22)

方程(2)可以写成:

-Δu+π=f∶=-ρut-ρu·u-d·Δd.

(23)

由Stokes方程的H2理论知:

因此,我们得到:

(24)

类似的,我们有:

‖u‖H3≤C‖f‖H1≤C‖f‖L2+C‖f‖L2≤C(M)+C‖ρ‖L6‖ut‖L3+C‖ρ‖L∞‖ut‖L2+

因此,很容易推出:

(25)

最后,我们得到:

(26)

结合(14)、(16)、(17)、(20)—(25)和(26),我们推断出(10)是成立的.

证明完毕.

致谢:感谢樊继山教授对本文的指导与帮助.