基于非线性混合效应模型的3个针叶树种削度方程研究

李春明 付 卓

（1.中国林业科学研究院资源信息研究所， 北京 100091；2.生态环境部卫星环境应用中心， 北京 100094）

编制科学合理的森林经营方案，需要编制通用性的材种出材率表[1-2]。削度是描述树干直径沿其树干向上随树干直径位置的升高而逐渐减小变化的程度，是用来说明干形变化的一种指标[3]。削度方程可以为森林经营者提供树干任意部位的直径、树干任意部分直径的高度、全树干材积以及从地面到任意高度的商品材材积[4]。构建树干削度方程已成为编制材种出材率表的首选方法和基础工作。在欧美等国家，树干削度方程已经逐渐取代材积表和材积方程[5]。因此，构建一个精度高的削度方程，可用较少的样木资料取得较为理想的结果，以满足生产上不同材种规格的需要。削度方程其主要形式有简单削度方程[6-9]、分段削度方程[10-14]和可变指数削度方程[15-19]。任何一个削度方程都不可能完满地描述所有树种树干形状的变化，同时也不会完全适应某一树种的所有林分。

在构建削度方程时，通常选择具有典型代表性样地中的多株树木，然后进行树干解析获取数据。这些树木由于所处环境不同，树木之间其形状会存在大的差异，另外数据存在着重复测量等特点。在构建削度方程时，存在着数据和统计上的挑战。混合效应模型方法能满足独立同分布的假设，能得到最好线性无偏估计，即能反映总体平均水平又能够体现林分或树木之间的差异，可以很好的解决削度方程中存在的上述问题。目前，国内外很多学者在构建削度方程时，已经考虑数据间存在的这些问题。例如基于混合效应模型方法的简单削度方程[20]，基于混合效应模型方法的分段削度方程[3,14,20-21]，基于混合效应模型方法的可变指数削度方程[22-25]。

本研究以吉林省汪清林业局96块云冷杉针阔混交林局级固定样地为例，构建云杉（Picea asperata）、冷杉（Abies fabri）和红松（Pinus koraiensis）等优势树种的削度方程。把3个树种的解析木数据分为两部分，一部分为模拟数据，一部分为验证数据（每个树种选择5株）。选择2种常用的削度方程，利用传统的拟合方法进行拟合，并在此基础上考虑样木水平的随机效应，构建基于混合效应模型方法的树干削度方程。选择均方根误差、绝对平均残差和确定系数等指标，对基于混合效应模型方法的削度方程与传统的削度方程拟合方法进行精度比较，最后确定理想的削度方程。

1 数据来源

本研究区位于吉林省汪清林业局金沟岭林场境内（43°17′～43°25′N，130°05′～130°20′E）。在1987年设立了96块云冷杉针阔混交林样地（20 m×30 m）。在设立的云冷杉针阔混交林中，以云杉、冷杉为主要优势树种，其他主要树种包括红松、白桦（Betula platyphylla）、水曲柳（Fraxinus mandschurica）、椴树（Tilia tuan）和色木槭（Acer mono）等。在每个样地中按红松、云杉和冷杉3种树种分别选择1株标准木作为解析木。解析木在伐倒后量测其胸径、树高和基部年龄。树木采用2 m 区分段，其各段分别在伐根0、1.3、3.6、5.6、7.6 m等位置截取圆盘，在最后一段不足2 m时，在高于上一段1 m处截取最后一个圆盘。对每1株树木分段测量各圆盘的带皮胸径和去皮胸径。由于一些解析木存在数据质量问题，最后共选择了82株云杉、95株冷杉和71株红松解析木数据。每个树种选择5株树木作为验证数据，其余作为模拟数据。树干材积采用平均断面区分求积式进行计算，3个树种的胸径、树高及年龄等信息见表1。

表1 云杉、冷杉和红松等3种树种树干解析统计Table 1 The statistical results of stem analysis for 3 species including P.asperata,A.fabri and P.koraiensis

2 研究方法

2.1 基础模型

本研究采用了2个常用的削度方程形式。第1个是Kozak等[6]在1969年提出的简单多边形削度方程，具体见式（1），文中简称F1。Max等[10]于1976年在Kozak等简单削度方程基础上发展出分段削度方程，具体见式（2），文中简称F2。2个削度方程的具体形式如下：

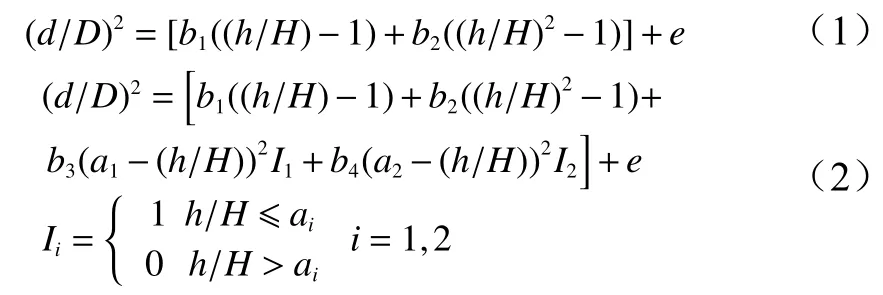
式中：d为树干h高处的带皮直径；D为带皮胸径；H为全树高；h为从地面起算到某一直径位置的高度。b1、b2、b3、b4为模型待估参数，a1、a2为树干下部和上部拐点处的相对高度。e为模型误差项。

2.2 非线性混合效应模型

非线性混合效应模型包括固定效应参数和随机效应参数两部分。在利用混合效应模型时，候选的削度方程一般表达形式如式（3）。

2.3 模型评价和检验指标

通常选择AIC信息准则（AIC）、BIC信息准则（BIC）和-2倍对数似然值（-2logL）等3个指标来比较模型间的拟合效果，评估模型对特定数据集的拟合优度，表示模型预测值与数据集中观测值之间的距离。指标值越小，说明模型的模拟效果越好[26]。选择似然比卡方检验（LRT）来比较模型之间的差异程度。

在对模型进行精度验证时，选择确定系数（R2）、均方根误差（RMSE）和绝对平均残差（）进行评价，如式（4）～（6）。

式中：esti为直径的预测值，obji为直径的测量值，为实测直径的平均值。N为所有解析木的总体圆盘数量，m为解析木数量，n为某一样木的圆盘数。

2.4 模型验证

在对模型进行验证时，传统方法需要根据估计出的参数来计算验证数据的均方根误差、绝对平均残差和确定系数。而混合效应模型需要计算验证数据中具体解析木的随机效应参数值，然后再计算均方根误差、绝对平均残差和确定系数。随机效应参数的计算方法可参考Vonesh等[27]，具体的计算公式如式（7）。

3 结果与分析

3.1 模拟结果

利用SAS的NLMIXED模块对Kozak 等[6]和Max等[10]的2个削度方程进行参数的拟合，具体结果见表2。利用确定系数、均方根误差和绝对平均残差计算误差，并利用LRT指标对传统削度方程模拟结果和基于非线性混合效应模型模拟结果进行比较，具体结果见表3。其中，Kozak等[6]的简单削度方程简称M1，Max等[10]的分段削度方程简称M2，Kozak等[6]的简单削度方程考虑随机效应的方程简称M1a，Max等[10]的分段削度方程考虑随机效应的方程简称M2a。

由表2～3可知，这2个削度方程均显示出较好的模拟效果，确定系数最小的为0.961 0，最大的为0.991 2。无论是云杉、冷杉还是红松，F2计算出来的确定系数都要高于F1，而均方根误差和绝对平均残差都要小于F1，这说明F2模拟效果要好于F1。这2个削度方程，无论拟合哪个树种，当考虑单木水平的随机效应后，均只有1个随机参数收敛，考虑2个或2个以上参数时，模型均不能够收敛。F1在参数b1上考虑随机效应的模拟效果要好于b2上考虑随机效应。F2在3个树种上的表现各不相同，在模拟红松时，b1的模拟效果最好。在模拟冷杉时，b4的模拟效果最好。在模拟云杉时，b2的模拟效果最好。所有3个树种，无论F1还是F2，在考虑随机效应后模拟效果均有所提高（AIC、BIC和-2logL等3个值降低），LRT值和p值 显示效果均达显著程度（α=0.05），并且确定系数、均方根误差和绝对平均残差也支持AIC、BIC和-2logL所获的结论。

表2 云杉、冷杉和红松3种树种不同削度方程的参数模拟结果Table 2 The parameters simulation results of different taper equations for 3 species including P.asperata,A.fabri and P.koraiensis

表3 云杉、冷杉和红松3种树种不同削度方程的模拟效果比较Table 3 The comparison of accuracy of different taper equations for 3 species including P.asperata,A.fabri and P.koraiensis

根据模拟结果，以相对高（树干任意高度/树高）为横坐标，相对直径（树干任意高度/树高）为纵坐标，选择最优的削度方程，绘制3个树种的树干曲线，具体见图1。很显然，对于3个树种来说，分段削度方程拟合效果很好。

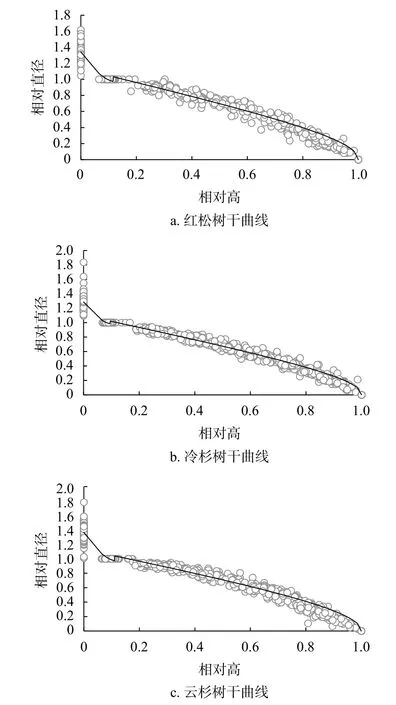
图1 云杉、冷杉和红松3种树种最优削度方程的树干曲线图Fig.1 Relative height plotted against relative diameter with a segment taper equation of 3 species including P.asperata,A.fabri and P.koraiensis

验证结果表明，与不考虑随机效应相比，当考虑随机效应后，除了红松的F2的绝对平均残差增大外，其余的确定系数均提高，而均方根误差和绝对平均残差都降低，符合上述的模拟结论。这3个树种无论哪个树种，F2的验证精度都要高于F1的验证精度，与模拟结论也一致。

3.2 模型验证

为了验证上述模拟结果，利用确定系数（R2）、均方根误差（RMSE）和绝对平均残差（）3个模型精度评价指标对验证数据进行计算。具体结果见表4。其中不考虑随机效应的模型（M1、M2）直接利用表2的参数代入公式结果。而考虑随机效应的模型（M1a、M2a），首先选择5株验证数据来估计每个样木的随机效应值，然后再计算3个评价指标。随机效应参数值的计算方法参考式（7）。

表4 云杉、冷杉和红松3种树种2种削度方程的验证结果Table 4 The validation result of 2 taper equations for 3 species including P.asperata,A.fabri and P.koraiensis

4 结论与讨论

本研究以云冷杉针阔混交林为例，选择云杉、冷杉和红松等3个主要树种的树干解析数据，采用了2种常用的削度方程形式，基于混合效应模型方法来构建削度方程。由于每个样地只选择了1株标准木，因此只选择了树木效应，将不同随机效应参数进行组合然后模拟，利用AIC、BIC和-2logL 3个指标来评价混合效应模型与传统方法的效果。结果表明：在2个以上参数进行随机效应组合时，模型均不能够收敛。这3个树种无论考虑哪种削度方程，在考虑混合效应模型方法后，AIC、BIC和-2logL 3个指标值均明显下降，说明混合模型的模拟效果都比传统模型的模拟精度高，利用确定系数、均方根误差及绝对平均残差 3个指标进行比较，无论是模拟数据还是验证数据均支持此结论。

1株树木从基部到顶部，可能由凹曲线体、圆柱体、抛物线体、圆锥体等一部分或几部分组成。因此，这3个树种，无论考虑随机效应与否，考虑2个拐点的Max等[10]的分段削度方程在模拟和验证中的精度都要高于Kozak等[6]的简单削度方程的模拟和验证精度。

本研究限于样本量，没有考虑样地水平的随机效应，也没有同时考虑两层次随机效应。另外本研究考虑了样木多次测量的异方差和自相关，但模型均不能够收敛，可能受限于样本量的大小，今后如果数据满足要求，可增加内容研究。另外树木的形状和林分密度、经营措施、树冠大小，甚至气候变化都有一定的关系，随着数据积累的增多，需要增加这方面的研究。