数学证明,在小学课堂真实发生
2021-01-11黄雅娓
黄雅娓

课前思考:
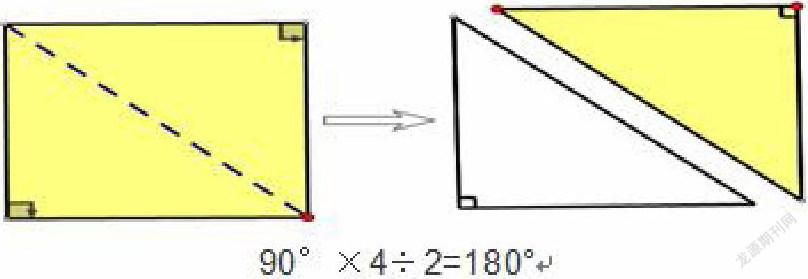
“三角形的内角和是 180°”,许多学生在课前都已经知道,但学生们只是停留 在“知道”这一层面。至于为什么内角和是180°,是怎么证明出来的,就不知其所以然了。而这节课采用的一般教学方法是先不外乎“量”、“拼”等实验验证,这属于不完全归纳法,课上研究的个例有限。法国著名数学家帕斯卡所提出的证明方法,从演绎证明的角度来推导三角形内角和,是很好的完全归纳。帕斯卡是这样证明的:长方形的四个角都是直角,四个角的和是360°;当长方形沿对角线一分为二后,就变成两个直角三角形,每个直角三角形的内角和就是360°÷2=l80°;任何一个锐角三角形或钝角三角形都可以沿高分为两个直角三角形,两个直角三角形的内角总和为180°+180°=360°,其中有两个直角(这两个不属于三角形内角)拼在一起成了一条直线,所以锐角三角形一个内角的和是360°-90°×2=180°;帕斯卡的證明过程中利用到了内角的变化,所以内角的概念是非常关键的。那么这节课能否抛开传统的“量、拼”等不完全归纳的方法,从数学演绎证明的角度“分割——转化——求证”,上成一节完全归纳的数学证明课呢?。
学习活动:
活动一:内角,变,变,变
师:这是一个三角形。谁来介绍一下你认识的三角形?
引出内角:刚才你们说的三角形有三个角,这三个角就是三角形的内角。这节课我们就重点来研究内角的变化。
师:观察谈论:看看,角1,角2,角3发生了什么变化。(用几何画板拉动三个内角)
师:观察四次变化的结果,你发现了什么?
生1:三角形的三个内角在拉动中,有内角变大,就会内角变小。
生2:无论怎么变,三个角的内角和是不变的,都是180°。
活动二:探究直角三角形内角和
师:三角形内角和是180°,你是怎么知道的?
学生起点:(1)书上看到或听说 (2)量出来 (3)三个内角拼成平角
(方法2和方法3不是这节要研究的主要方法,不作为主讲方法。)
(4)长(正)方形四个角都是直角,就是4个90°,对半切一半就是180°。
师:所有直角三角形的内角和都可以用这样的方法(4)来验证么?怎么证明?
生:所有的长方形都可以沿着对角线分割成两个完全一样的直角三角形。
小结:刚才我们运用了转化思想,把长方形分割成两个直角三角形,从而求证出直角三角形的内角和,看来“转化——求证”这是数学学习的一个好方法。
活动三:练习与拓展
练习一:基础练习,你能求出三角形第三个角么?(略)
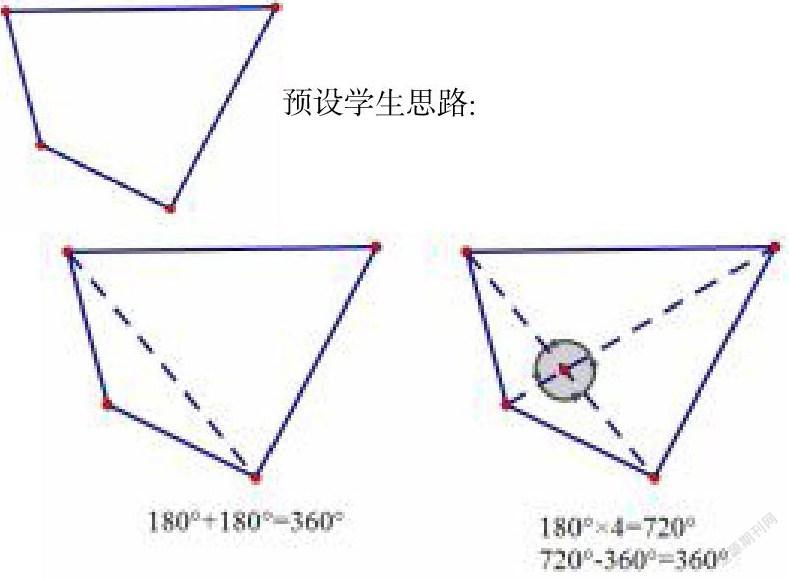
练习二:你能算出四边形的内角和么?把你的想法画一画,算一算。
练习三:如果给你五边形、六边形,你打算怎样求它们的内角和?用这样的证明方法你还能求什么图形的内角和呢?
预设学生思路:
总结:课前还有同学提出三角形内角和可以用度量角或者把三个内角拼成一个平角的方法,感兴趣的同学可以回家试试,看看不一样的思路又是怎么研究三角形的内角和的!
课后反思
本堂课的教学设计,很明显有两个“变”和一个“不变”。
一、变:从“实验证明”到“数学证明”
本课最突出变化是课堂上没有用传统研究方法“量”和“拼”,“ 量”容易有误差,“拼”破坏了原有三角形的完整性,这两种方法都属于实验证明。而本课采用了法国著名的大数学家帕斯卡数学证明的方式来研究三角形内角和。有些老师可能为认为这种推理证明的方法太难,不大适合小学生,然而事实上学生们是有这方面的准备的,在长方形和直角三角形中已经积累了一定的严格证明的活动经验。针对本节课知识层面不难的情况下来经历一场数学证明的头脑风暴,感受数学的严密性与逻辑性,给学生更加严谨的数学素养熏陶,不外乎是一次很好地机会。而内角概念的建立成了本课的研究起点。在三角形的角拉动的过程中,感知一个内角变大(小),另两个内角就会变小(大)。但是无论怎么变,三角形的内角和是不变的。整个证明过程,我们从特殊三角形(直角)入手,这是最接近学生知识本源的地方,慢慢扶着,一步一步,学生在经历数学证明的过程中,感受数学本身真正的魅力,并为后续的普通三角形的证明打下基础。
二、变:从“不完全归纳”到“完全归纳”
“量”“拼”等实验验证的方法都是对个例进行研究,一堂课所能研究的个例毕竟有限,严格意义上来说,这时候得到的,还只是一种规律、一种猜想,还需要经过数学的严格证明,或者大量的实验论证然后才能运用,这就是“不完全归纳”,而小学阶段大部分的探索研究都属于“不完全归纳”。而本课的教学设计,从特殊三角形(直角)入手,先研究了所有的长方形都能分割成两个直角三角形,从而得出所有其内角和,紧接着运用本结论来求证锐角和钝角三角形的内角和。所有的锐角或钝角三角形都能分割成两个直角三角形,得出这两种三角形的内角和。又因为三角形按角分类属于完全分类,从而得出所有的三角形的内角和,这就是一个完美的“完全归纳”的过程,开阔了学生的眼界,再一次体验到数学求证的严谨美!
三、“不变”: “转化——求证” 一路相随
整个课堂,无论是教学直角三角形内角和,还是独立研究锐角、钝角三角形,又或者是后面的放手拓展四边形形内角和,更或者是五边形、六边形……我们可以感受的是里面所蕴含的最本质的数学思考方法是不变的,那就是“转化——求证”,这条暗线一直贯穿整堂课。数学证明过程是有思维含量的,但是学生们是有“法”可依,有章可循,并能发现用这一方法可以解决所有多边形内角和。在这一过程中,学生的数学思维得到真正的一次历练,空间观念和转化思想得到大幅提升。
完全归纳的数学证明课在小学课堂上是少之又少,因为这不仅需要教师的自身数学素养,也需要学生具有一定的数学求证思维和空间观念,而这不是一蹴而就的,正需要我们珍惜每一次机会,为学生慢慢铺好求证道路。
