分位数回归模型对国内大宗商品指数市场风险的度量
2021-01-11杨立建
杨立建


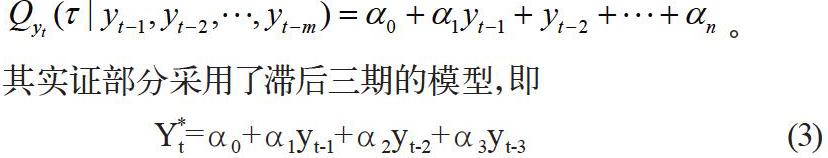
摘 要:本文通过建立基于分位数回归的VaR模型,对国内具有代表性的大宗商品期货价格指数市场风险进行了度量,实证分析了大宗商品期货价格指数具有尖峰厚尾、聚集效应的特性;同时,进一步拓展了基于分位数回归模型来测度在险价值(VaR)的方法。
关键词:分位数回归;VaR;大宗商品期货价格指数;市场风险
中图分类号:F252.5 文献标识码:A 文章编号:2096-0298(2021)01(a)--03
市场风险指的是由于金融市场上标的产品价格波动而导致的风险,又称为价格波动风险。市场风险是金融衍生品交易中经常面对的一种风险。随着我国金融市场改革创新的进一步推进,2019年8月,我国首批商品期货指数ETF基金获得证监会批准,大量的原先投资于股票和债券的机构投资者和普通投资者有机会通过这类公募基金产品,参与到大宗商品期货交易中。由于商品期货市场与股票市场的交易机制不同,商品期货市场是多空交易机制,交易方式是保证金交易,具有高杠杆、高波动等特征,其时间收益率序列一般都具有尖峰厚尾效应、聚集效应和时变方差特性,因此,投资者准确的识别和度量其市场风险尤为重要。
1 在险价值理论简述与分位数回归模型
在险价值(Value at Risk)方法是金融风险度量的方法之一,通常将在险价值(VaR)定义为某一置信水平下,某一金融资产或证券组合价值在未来特定时期内的最大损失。计算公式为:
其中P0为标的产品的初始价值,在一定的置信水平下,P*为该标的资产最低的期末价值。只要知道一定置信水平下的最小收益率r*和该投资标的资产的初始价值P0,便可以求得P*。
计算VaR方法有很多种,但使用分位数回归模型计算VaR的方法正在受到许多学者的重视,并在不断研究与发展中。分位数回归,是估计一组回归变量X与被解释变量Y的分位数之间线性关系的建模方法,强调条件分位数的变化。第τ个百分位数表示因变量的数值低于这一百分位数的个数占总体的τ%。国内对分位数回归模型计算VaR研究比较多的是基于Taylor(1999)[1]的文献,Taylor(1999)将分位数回归应用到VaR计算的表达式为:
张海云(2011)[2]借鉴其研究思路,将收益率作为被解释变量,和K作为解释变量,通过分位数回归进行拟合。假设持有期K=1,将模型简化为:
扶仕彤,金良琼(2019)[3]将滞后期收益率作为解释变量,建立分位数回归模型来估算最小收益率r*的值。模型为:
其实证部分采用了滞后三期的模型,即
以上是基于分位数回归模型来计算单期VaR值的两种思路。本文沿袭Taylor(1999)的主要观点:预期波动率(或条件标准差)在计算VaR值时是重要的变量。实际计算中,预期波动率σt的获得也并非只能通过GARCH模型。国外学者研究的实际波动率(RV)和已实现极差方法(RR);国内学者赵树然等(2012)[4]基于高频数据与极值理论整合的CARR模型都是获得预期波动率的方法。因此,本文将预期波动率(或条件标准差)作为解释变量,与其他滞后期收益率组合,建立分位数回归模型。模型如下:
其中,Y*t是需要计算的最小收益率r*,σt是条件标准差。β0、β1、β2、β3是待估参数。
2 实证结果与分析
本文采用的数据是南华商品指数、上海期货交易所有色金属指数、郑州商品交易所易盛能化A指数。本文选用的数据为2014年12月31日至2019年12月31日共1220个交易日的收盘价,由此計算每个交易日的收益率,可得到样本的收益率时间序列,收益率Rt=lnpt–lnpt-1,pt为交易日的收盘价,pt-1为上一个交易日的收盘价。数据来自WIND咨询软件及各期货交易所网站。计量软件使用EVIEWS8.0。
2.1 数据的描述性统计
各个期货指数收益率时间序列的分布特征对VaR值的计算和度量模型的选取很重要。
对于期货指数日收益率序列,偏度都等于零,说明序列分布是对称的,偏度小于零,说明序列分布有左拖尾,否则有右拖尾。标准正态分布的峰度为零,峰度明显不等于零,说明收益率序列有尖峰或平峰的特征。在正态分布的假设下,JB统计量服从自由度为2的卡方分布,否则,拒绝原假设。从以上描述性统计表可知,各个期货收益率序列均不服从正态分布,如果采用传统的VaR方法估计收益率风险会有偏差。
2.2 平稳性检验
本文采用ADF 检验方法对于时间序列需要进行平稳性检验。检验结果如下。
从表2可以看出,各期货指数收益率序列的t统计量值全部都小于显著性水平为1%的值,这表明可以在99%的置信水平下均拒绝存在单位根的假设。因此,各序列是平稳的。
2.3 ARCH LM效应检验
对于各期货指数收益率时间序列ARCH 效应检验的计算结果如表3所示。
检验结果表明,各期货指数的收益率残差序列存在ARCH效应,即呈现出集群效应。
2.4 建立GARCH(1,1)模型
由于要计算波动率σt,本文建立GARCH(1,1)模型,并选择GED分布来计算。结果如表4所示。
由表4可知,GED自由度值都小于2,表示尾部比正态分布更厚;α+β<1,说明了GARCH模型的方差值有均值回归特性,残差序列的异方差函数具有长期相关性。
2.5 在险价值VaR值的计算
本文式(1)分位数回归模型计算VaR的公式为:VaRt=-Pt-1r*。
其中,r*是分位数回归模型计算的最小收益率;Pt-1是各期货指数前一天的收盘价。
2.6 失败天数与返回检验
失败天数的判定标准:当VaR>Pt-1-Pt时,判定成功,失败天数加零;当VaR LR统计量应该服从1个自由度的卡方分布,当失败发生的次数很高或很低时,式 (5)计算的LR统计量会较大。在1个自由度的卡方分布中,LR统计量大于3.8415的概率为5%,因此,当计算的LR统计量大于3.8415时,可以拒绝模型。 返回检验选取的数据为2018年1月1日起到2019年12月31日止,共计486个数据。 由表5可见,式(2)与式(4)返回检验的LR统计量都小于3.8415,说明模型有效。式(3)的LR统计量大于3.8415,可以拒绝模型。 3 结语 本文运用ARCH模型相关理论和在险价值(VaR)理论,对国内大宗商品期货价格指数的市场风险进行度量后,结果显示各期货指数波动的风险具有多数金融产品价格波动的尖峰厚尾、聚集效应的特性,在实际金融投资过程中应引起重视,适时调整投资策略,降低投资风险。同时,本文拓展了分位数回归模型计算VaR值的方法,将滞后期收益率和预期波动率组合成新的模型,并对新模型进行实证检验,取得较好的结果。 参考文献 Taylor J W. A quantile regression approach to estimating the distribution of multi-period returns[J]. Journal of Derivatives, 1999(7):64-78. 张海云.论分位数回归在计算VaR中的应用[J].现代商贸工业,2011,023(015):185-186. 扶仕彤,金良琼.基于分位数回归模型的VaR研究——以贵州百灵股票为例[J].统计学与应用,2019,008(002):364-369. 赵树然,任培民,赵昕.基于CARR—EVT整体方法的动态日VaR和CVaR模型研究[J].数量经济技术经济研究,2012,029(011): 130-148.
