中国碳金融市场风险度量

摘要：碳金融业务随着低碳经济的深入人心而迅猛发展，然而制约着碳金融服务机构实现创新的是市场风险，因此，将市场风险控制在合理的范围内至关重要。本文选取的数据样本为2013年6月18日至2015年12月31日的碳交易均价和欧元兑人民币汇率数据，用Copula函数构建模型计算中国碳金融市场的风险，并提出政策建议。

关键词：碳金融；市场风险；Copula

1.引言

低碳经济的兴起促进了碳交易市场的蓬勃发展，碳金融业务创新也随之兴起。以兴业银行为主的商业银行主要参与清洁发展机制项目，市场风险受国际汇率影响较大，碳排放交易所交易试点主要交易对象为CCER，主要受碳价波动影响。由此，本文在考虑不同因子之间的相关性后，选取Copula函数构建模型这种非传统度量方法来计算碳金融业务的市场风险。

韦艳华等国内外专家在考虑变量的相关性后，把Copula函数应用到以GARCH构建的金融变量边际分布的模型中，研究变量相依性以及整合后的市场风险。周艳菊等基于贝叶斯网络并利用Copula方法度量了我国商业银行在不同置信水平下操作风险损失的VAR和CVAR值，该成果的发表为更准确的度量操作风险提供了依据。李建平等考虑风险相关性后对商业银行主要面临的三类风险：市场风险、信用风险和操作风险进行了集成，实证显示考虑相关性后的VAR值比直接相加的VAR值要小，为研究金融市场整体风险提供新思路。张晨等根据对商业性银行介入碳交易业务所面临的市场风险构建的以Copula为基础的模型的结果，认为政府监管对减少碳交易风险起到一定的作用。总体而言，Copula的性质是在非线性单调变换下函数不变，因此，可以对非线性、非对称性的相关模式进行刻画，并且实现风险分散。

2.模型构建

本文利用Copula函数对中国碳金融市场的风险进行度量。当使用Copula函数计算市场风险时，主要体现在与VAR度量方法的结合上。Copula将不同的金融资产的边际分布连接起来，得到它们的联合分布，从而据此计算相应的分位数，得到的值也就是市场风险值。假设，F是由Copula函数连接的边际分布的联合分布函数，则对于显著水平的VAR值计算如下：

运用Copula函数构建模型后，拟合不同形式的Copula函数时需要对参数进行估计。本文采用非参数核密度估计法，具体步骤如下：

（1）利用核密度函数得到A、B两类因子的非参数核密度估计为：

（2）Copula函数中均匀边际分布变量是根据密度函数算出的分布函数得到的，即：

由上述公式得到的是Copula函数中的估计值。

（3）不同Copula函数的参数利用极大似然法估计，即：

（4）这样不同的Copula结构可以得到不同的Copula函数，即：

3.实证研究

文章选取2013年6月18日至2015年12月31日的中国七所碳交易试点碳交易均价和欧元兑人民币汇率的收益率数据共579组，作为样本，数据来源于wind。碳交易均价定义为：

上式中角标分别代表北京、上海、深圳、湖北、广州、天津、重庆等地。本文将收益率定义为（i=1碳价，i=2汇率）：

3.1变量的基本统计特征

经过ADF检验，两个收益率序列都是平稳序列，如图1的时间序列图形显示，两个收益率序列围绕着均值上下波动，且其波动性具有显著的“集聚效应”。下表给出两个序列的一些统计特性：

从上表可以看出，两序列的均值和标准差都较小，偏度值比0大，为右偏，峰度值比3大，表现出“尖峰厚尾”的特征。对碳均价和汇率两收益率序列进行正态性检验，得出H=1，即拒绝原假设，认为他们不服从正态分布。

3.2参数估计

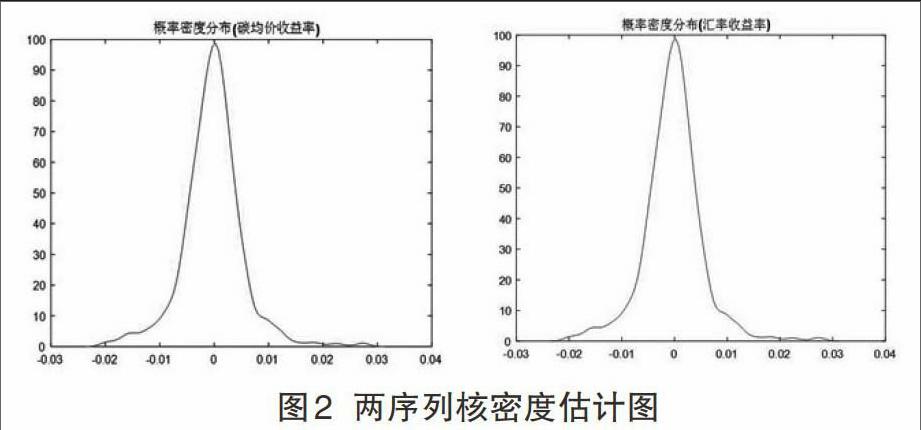
Parzen（1962）的研究结果显示了核密度估计具有渐进相容性和渐进正态性的特征。这里选定正态核函数，由正态核的经验法则选取光滑参数，就可以计算碳均价和汇率收益率的非参数核密度估计的光滑参数分别为，，其图形如下：

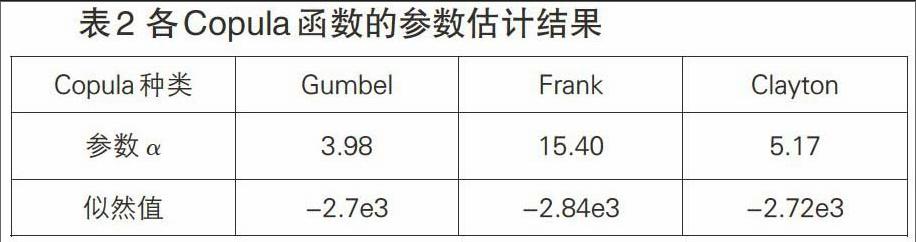
从图2可以看出核密度估计函数基本上拟合了收益率分布的“尖峰厚尾”特征。根据公式可以计算出Copula函数中的估计值。为了验证，是来自上的均匀分布，画出经验分布与均匀分布的累积分布函数图，图形基本重合。由此得出，确实来自均匀分布。接着求出阿基米德 Copula中各参数估计值。结果如下：

对比上表中各Copula函数的参数值和极大似然值，不难看出Frank函数对应的参数较大，因此初步断定Frank Copula能够描述两序列之间的相关关系。

3.3Copula函数选择

本文根据非参数核密度估计方法计算出了不同阿基米德 Copula的参数估计值。但是这些不同的阿基米德Copula函数中是不是Frank能更准确地刻画两序列之间的相关结构，还需要进一步的检验。本文采取三种函数与均匀分布之间的欧式距离比较，得到如下结果：

从上表中我们看出Frank是最优的，而Gumbel和Clayton函数距离相对较远。因此，在显著性水平为5%情况下，认为两序列的相关结构可以指定非线性的Frank函数描述。进一步计算阿基米德 Copula函数的相关性测度的指标：

从表4中我们看出基于阿基米德 Copula函数的相关性测度指标中Frank的Kendalls Tau和Spearmans Rho是最高的。也就意味着Frank对极端事件的尾部相关性能够更好地加以描述，所以它更能恰当地刻画两序列的相关性问题，碳均价和汇率收益率序列整体相关性比较强，与上面的非参数密度实证结果相符。

3.4市场风险VAR

为了得到市场风险的具体数值，对碳均价和汇率收益率进行等权重组合，运用Frank Copula进行蒙特卡罗模拟，计算出不同置信度下的值，结果见下表：

实证结果比较可知：置信度的提高带来VAR的值的增大；碳均价序列的VAR值相比汇率序列的VAR值要大；汇率是受到政府监管的，而碳价监管还未完善；若将两风险的VAR值直接相加要比整合后的VAR值要大，说明不同的风险因子之间的相关性会使市场风险的值变大；而蒙特卡罗模拟的值处于两者之间，市场风险VAR值随着蒙特卡罗模拟模拟的次数增多而增大；由此可知，本文选取的Copula模型很好地将序列间相关性整合在一起，对中国碳金融的市场风险进行了很好的度量。

结论

低碳经济的兴起促进碳金融业务迅速崛起，碳金融服务机构的业务的发展同时也促进经济转型，参与碳金融业务的关键就是有效地实现碳交易市场的风险防控。本文根据研究结果，现提出如下政策建议：

首先，积极构建全国范围内较为完善的碳金融交易平台。一是，统一定价，在全国范围内实现统一制定价格，有明确对的价格制定体系，从而提高碳金融交易的市场效率。二是，统一配额，在全面推进碳金融交易平台建设的基础上，实现全国范围内的总量控制。三是，统一监管，实现自上而下的审慎监管体制，明确各级部门监管范畴，并防止冲突。

其次，健全交易和监管机制。设立碳排放权交易所交易的进入门槛，确保交易主体具有良好的风险防范和控制意识，同时设立风险警示制度，通过保证金制度，实现对交易风险的防范。

最后，与国际碳排放交易体系加强合作。对国内相对分散的碳金融交易平台进行深度整合，重点扶持碳金融交易的第三方机构，加强与国际化程度较深的气候交易所的合作，逐步实现中国碳金融交易的国际化。

参考文献：

[1]韦艳华，张世英.金融市场的相关性分析——Copula-GARCH模型及其应用[J].系统工程，2004，22（4）：7-12.

[2]周艳菊，彭俊，王宗润.基于Bayesian-Copula方法的商业银行操作风险度li量[J].中国管理科学，2011，19（4）：17-25.

[3]李建平，丰吉闯等.风险相关性下的信用风险、市场风险和操作风险集成度量[J].中国管理科学，2010，18（1）：18-25.

[4]张晨，杨玉，张涛.基于Copula模型的商业银行碳金融市场风险整合度量[J].中国管理科学，2015，04：61-69.

[5]柏满迎，孙禄杰.三种Copula-VaR计算方法与传统VaR方法的比较[J].数量经济技术经济研究，2007（02）：154-160.

作者简介：

韦景梅（1989.11- ），女，汉族，河北邢台人，硕士研究生在读，现就读于河北工业大学经济管理学院，应用经济学专业金融学方向。