基于多种群协同进化算法的混合交通流信号优化

陈 娟,荆 昊,方宇杰

(上海大学悉尼工商学院,上海201800)

在我国,由机动车、非机动车、行人形成的混合交通流,是造成交叉口交通拥堵的主要原因之一.研究混合交通流的实时变化性,设计出适合我国混合交通流的优化目标和优化控制方法,对解决我国城市交通拥挤问题有非常重要的现实意义.

随着交通拥堵问题的日益严重,学者们意识到了混合交通流的复杂性,在混合交通流模型方面进行了相关研究.Xie等[1]在Nakayama等[2]的2维最优速度模型的基础上,提出了一种2维跟车模型,用于描述包括机动车和非机动车的混合交通流的特征;Mu等[3]利用元胞自动机模型,对传统汽车和微型汽车组成的混合交通流进行了分析;Luo等[4]研究由不同类型的车辆组成的混合交通流的操作特性,设计了元胞自动机模型,以描述双向道路上的物理特性和不同车型的机械特征;Li等[5]利用元胞自动机建立了交通流模型,研究了在不同延迟概率下混合车流的车辆间隙分布,以及给定车辆密度的不同混合率.以上研究都只对机动车和非机动车进行研究,并未考虑行人的影响.Sharma等[6]指出,人为因素在理解交通流动态以及对混合交通流的有效操作和控制方面起着关键作用,并研究了行人在混合交通流中的作用,但该研究只是从行人的角度出发进行研究,并未综合考虑机动车、非机动车、行人三者之间产生的共同影响.

由于实际交通系统具有动态性、非线性、模糊性等特点,相比定时控制和感应控制,智能控制能表现出更好的效果[7].交叉口智能信号控制方法主要包括专家系统、模糊控制、人工神经网络和进化算法等.但是,模糊控制中模糊规则及隶属度函数选择的难度较大;而人工神经网络需要大量的训练及测试数据,且训练时间长.

混合交通流环境下的信号配时问题,是一个典型的动态、高维、多目标优化问题.进化算法计算速度较快,能较好地保留解的多样性,在该领域得到了广泛的应用.王磊等[8]将总延误时间、总停车次数、总通行能力这3个指标作为优化的对象,将多目标优化问题转换为单目标优化问题,采用单目标方法进行求解,从而使得部分指标实现局部最优,但无法得到在所有目标上同时达到最优的信号配时方案;Shou等[9]建立了非饱和交叉口信号控制多目标动态决策模型,对信号周期时长、绿信比和相序3个信号配时参数同时进行优化,并应用混合遗传算法求解最优决策变量;吴金顺[10]综合考虑信号交叉口通行能力最大、车辆平均延误最小、交叉口停车次数最小这3个指标,建立了一个多目标信号配时模型,采用遗传算法求解在该模型下的最优绿灯配时方案,并与经典Webster模型及不考虑平稳性的基础模型进行比较,结果表明该模型的平均延时略长于Webster延误模型,但平均停车次数和流量均优于Webster.陈娟等[11]提出了一种基于迭代预测非支配排序遗传算法(iterative predictive nondominated sorting genetic algorithm-Ⅱ,IPNSGA-Ⅱ)的多目标相容控制方法,用于处理在过饱和状态下相邻交叉口的信号控制问题,提出的相容控制算法具有鲁棒性、实时性、动态性的特点,能较好地处理有冲突的多目标控制问题,但模型仅考虑了机动车效益指标,没有同时优化非机动车和行人的通行效益;沈峰等[12]将交通流模型嵌入到多目标优化算法中,替代以往传统的目标函数,直接采用静态多目标优化算法NSGA-Ⅱ进行求解,解决信号配时问题,但该算法并没有考虑在动态需求环境下NSGA-Ⅱ算法收敛速度变慢的问题.

目前,有关在混合交通流环境下信号配时问题的研究主要存在如下问题:①在模型研究方面,综合考虑机动车、非机动车、行人三者产生共同影响的模型的相关研究较少,尤其是在非机动车和行人方面的研究更少;②在考虑多目标优化性能指标方面,绝大多数的研究仅考虑机动车性能指标,较少考虑机动车、非机动车和行人的综合性能指标;③在解决方法方面,虽然大多数的研究考虑了多个性能指标,但是采用的解决方法,不是把多个目标进行加权,转化为单目标问题进行求解,就是采用静态多目标优化算法来解决多目标优化问题,而这些方法都只考虑2个性能指标,很少涉及3个及3个以上的目标.而NSGA-II算法在解决高维多目标优化问题的时候,计算效率低,收敛速度慢.

在混合交通流下的信号配时问题,其本质是一个非常典型的动态、高维、多目标优化问题,因此无论是采用单目标优化方法,还是采用常规的静态多目标优化算法,都不能得到满意的效果.

针对以上问题,本工作根据机动车、非机动车、行人延误时间这3个目标,建立了相邻交叉口动态多目标优化配时模型,并且提出了基于多种群协同进化的动态多目标优化算法(multipopulation coevolutionary dynamic-multi-objective genetic algorithm,MPCED-MOGA),对在混合交通流环境下信号配时多目标优化问题进行求解,并在测试函数和仿真环境下进行了验证.

1 多种群动态多目标进化算法

多种群方法属于协同进化理论.协同进化算法分为3种:基于种群间竞争机制的协同进化算法、基于种群捕食机制的协同进化算法和基于种群共生机制的协同进化算法.

1.1 多种群协同进化方式

本工作提出的多种群协同进化算法包含2个种群,即搜索种群和跟踪种群.搜索种群用来寻优,且只在环境发生显著变化时进行目标函数重估.跟踪种群跟踪环境变化,且随环境变化目标函数不断进行更新.在进化过程中,跟踪种群不断把收敛到的较优解分享给搜索种群.图1给出了2个种群间的工作机制.

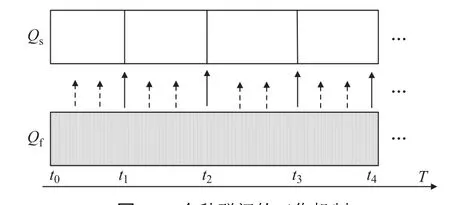
图1 2个种群间的工作机制Fig.1 Working mechanism between two populations

图1中,Qs、Qf分别为搜索种群和跟踪种群,种群规模为pops、popf,种群规模一般设定pops:popf=2∶1.随着时间的推进,跟踪种群不断更新自身的适应度值;只有当环境变化检测因子检测到环境发生显著变化时,Qs才进行目标函数的更新.2个种群的交互机制如下:当进化过程处于2次环境变化之间时,跟踪种群不断把自身的最优解分享到搜索种群中,以增加Qs最优解的质量.如当时间t∈(t0,t1),Qf分享r·popf的个体到Qs中(r为交互比例,本工作设r=0.5).当t=t1时,环境变化检测因子检测到了环境的变化,算法储存此时的Qs解,作为时间t∈t0算法输出的最优解,同时把Qf中的所有解作为Qs在t∈t1时的初始解.随着时间不断的推进,2个种群按上述机制不断进行更新.

1.2 多种群协同进化过程

通常,任何静态多目标算法加上动态多目标协同进化机制都可以解决动态多目标优化问题.本工作提出的MPCED-MOGA算法步骤如下.

步骤1初始化搜索种群和跟踪种群,种群规模分别为pops、popf;进化代数gen=1;环境变化参数为nt,τt;环境变化阈值为δ;最大环境变化次数为Timemax;初始化搜索种群和跟踪种群的时间参数为ts和tf,且ts=tf=0.

步骤2分别对2个种群进行遗传、变异操作,并从跟踪种群中选出r·popf个体加入搜索种群中,对2个种群进行非劣排序后更新.

步骤3如果Time=Timemax,则输出搜索种群中每个环境状态下的最优Pareto最优解为,结束;否则,转步骤4.

步骤4令tf=tf+1/(ntτt),重估跟踪种群的目标函数值.

步骤5在gen为τt的整数倍数的情况下,根据环境变化检测因子判断环境是否发生变化.如果没有发生变化,则转入步骤2;如果发生了变化,则记录下搜索种群中当前最优解,令Time=Time+1,,转入步骤6.

步骤6对跟踪种群进行交叉变异,得到pops规模的种群对搜索种群实现完全替代,转入步骤2.

图2给出了MPCDE-MOGA算法的流程图.

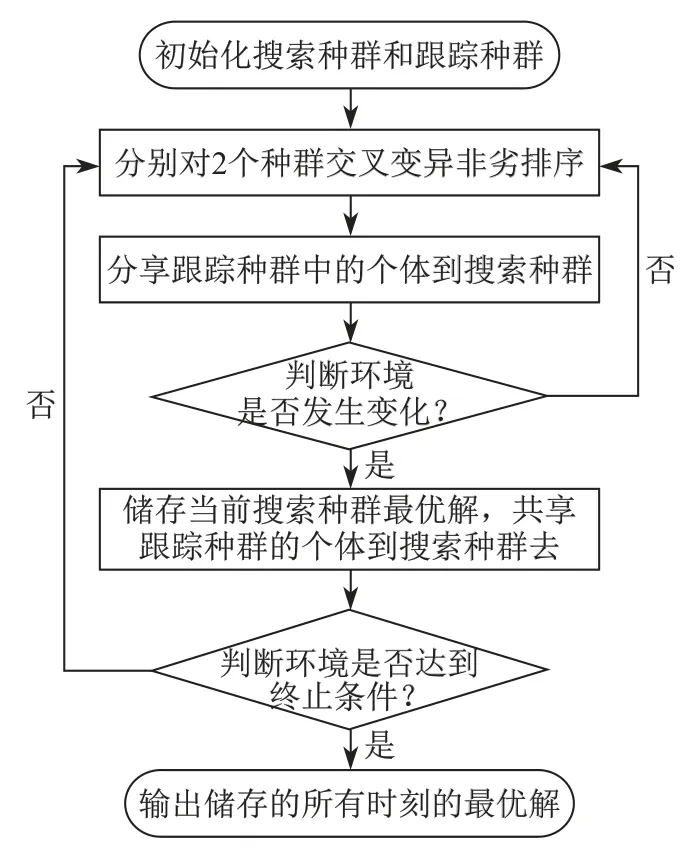
图2 MPCDE-MOGA算法流程图Fig.2 MPCDE-MOGA algorithm flow chart

2 信号配时多目标优化模型

本工作对共信号周期时长、绿信比和相位差进行了优化.优化的性能指标有机动车延误、非机动车延误和行人过街等待时间.

2.1 机动车延误

结合图1,在相邻交叉口协调控制中,机动车延误分为外部进口道延误与内部进口道延误[13].外部进口道延误公式参照《道路通行能力手册》[14]:

式中:d为交叉口每辆车平均信号控制延误;d1为车辆在均匀到达时的信号控制延误;d2为车辆随机到达并引起超饱和情形所产生的附加延误;d3为初始排队附加延误,即在车辆延误计算初期,因上一时段留下积余车辆而使后续车辆产生的附加延误.

本工作采用陈小红[13]提出的模型进行内部进口道延误的计算.车流在驶入下游交叉口时遇红灯受阻,此时分2种情况:①车队头车到达下游交叉口时遇红灯受阻,称为车队头车受阻;②车队头车到达下游交叉口时遇绿灯,由于交叉口信号切换为红灯,使得车队后部车辆交通流受阻,故称为非头车受阻.

(1)车队头车受阻机动车延误.

不考虑下游交叉口积余车辆的影响,如果车队头车在两交叉口a、b间的行程时间大于相位差与绿灯之和,说明在车队头车到达下游交叉口时,信号绿灯时间已结束,车队需排队等待.此时车队头车受阻,根据车队到达规律,延误计算为

(2)车队非头车受阻机动车延误.

当车队头车在两交叉口间的巡航时间小于相位差与绿灯时长之和,且大于相位差时长时,车队头车到达下游交叉口时信号灯为绿,此时车队头车可顺利通过交叉口,但车队非头车部分可能受阻.根据车队到达规律,其车辆延误为

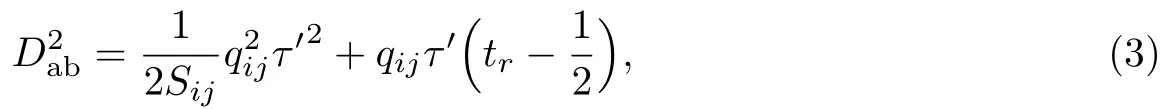
2.2 非机动车延误

设qb为下游交叉口的自行车到达流量;为信号红灯时间;为信号绿灯时间.当下游交叉口绿灯亮起后,车辆以饱和流量驶离交叉口.由于启动波的影响,仍有车辆在队尾继续停下来等待通行,经过M秒启动波追上停车波,之后绿灯时期到达的N辆车辆连续通过交叉口.根据交叉口驶入与驶离的车辆数相等的原理,可得非机动车延误db[13]:

2.3 行人过街等待时间

本工作假设交叉口行人的到达是均匀的,则行人的平均等待时间仅与其所用信号灯的红灯时间有关[13],

式中:tR为行人过街信号红灯时间.

2.4 相邻交叉口动态多目标优化配时模型

上述3项评价指标分别从不同的角度反映了信号配时效果,在混合交通环境下相邻交叉口动态多目标优化配时模型为

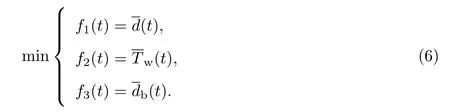
约束条件描述如下:

(1)相邻交叉口相位差不应不大于公共信号周期,即

(2)交叉口周期时长应大于各相位的有效绿灯时间之和为

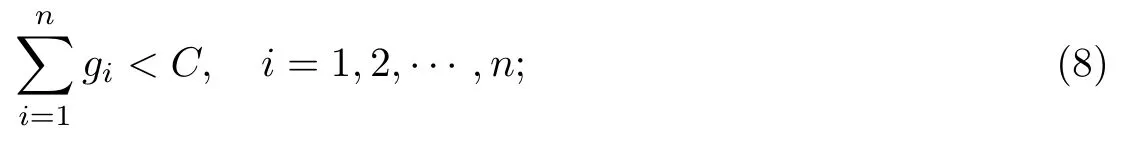
(3)各相位机动车车流量最大饱和度Xi满足

式中:qi为第i相位车辆实际流量;qsi为第i相位饱和流量.

3 实验研究

3.1 测试函数结果分析

本工作在Farina等[15]给出的3个测试函数下进行测试,采用反世代距离(inverted generational distance,IGD)评价指标和空间(Spacing,Sp)分布范围作为算法的收敛性和分布性性能评价指标.将本算法与3种典型动态多目标算法的优化结果进行对比.这3个算法分别为Deb等[16]的动态多目标优化算法DNSGA-Ⅱ-A、DNSGA-Ⅱ-B和Hatzakis等[17]提出的基于简单预测的动态多目标进化算法DNSGA-Ⅱ-PREM.

算法的参数设置如下:种群规模N=150;交叉概率为0.9;变异概率为1/n,n为决策空间的维数.本工作提出的MPCED-MOGA算法的搜索种群规模为100,跟踪种群规模为50,交叉概率和变异概率同上.为了研究在不确定环境下各种算法动态变化的影响,本工作给出了不同的(τt,nt)组合,对每个问题的各种组合都做了20次独立实验,即各种算法统一跟踪20次环境变化,环境变化的阈值设为0.01.

将4种算法在解决不同动态多目标优化基准问题的收敛性和分布性的结果进行对比分析.在分析算法结果时,考虑到不同算法输出的最终满意解的个数不等,为了保证最后进行对比分析的种群数量相等,本工作从DNSGA-Ⅱ-A、DNSGA-Ⅱ-B、DNSGA-Ⅱ-PREM每次变化输出的150个种群中,根据非劣排序与拥挤距离选出100个较优个体进行分析.表1和2分别为4个算法独立运行20次的收敛性指标IGD指标和分布性指标Sp的统计结果.表中(nt,τt)表示为环境变化的频率和幅度;Mean代表各算法当前指标的均值,std为各算法当前指标的标准差.从表1中可以看出,对于3种不同的测试函数,MPCED-MOGA相对于其他算法收敛到不错的结果;从表2可以看出本工作提出的MPCED-MOGA在具有较好的追踪性能的同时,分布性能也是不错的;对于不同的(nt,τt)对,MPCED-MOGA都获得了较好的效果,说明算法在不确定环境下能够对环境的改变做出快速反应,同时能快速地向问题的最优解集靠近.

表1 独立运行20次算法IGD指标Table 1 IGD values of algorithm running independently for 20 times

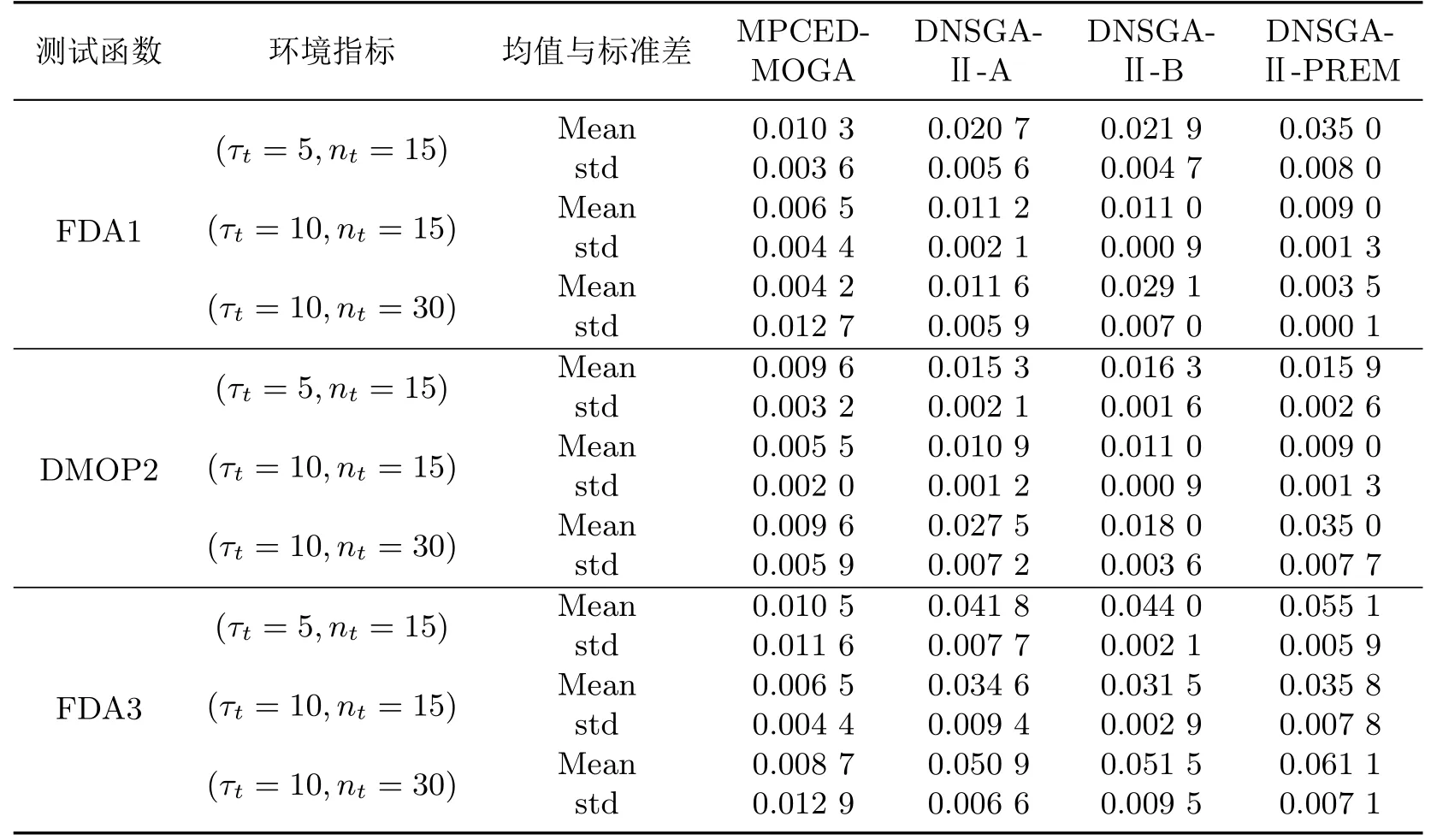
表2 独立运行20次算法Sp指标Table 2 Sp values of algorithm running independently for 20 times

对于FDA1函数,实验结果证明,在不同的环境变化情况下MPCED-MOGA的性能是最好的.图3是测试函数FDA1在(nt,τt)为(5,30)时,环境变化5次的结果.图3给出了4种算法所得的Pareto前沿与其真实Pareto前沿的对比图.由于该测试问题的真实帕累托最优前沿(Pareto optimal front,POF)是不变的,本工作对不同时刻的目标函数值进行了平移.令(F1+t/5,F2+t/5),其中t表示为不同时刻.显然MPCED-MOGA在5个不同的时刻都比其他3个算法的收敛性能优越,其收敛得到的最优解集与FDA1真实解的距离最近.

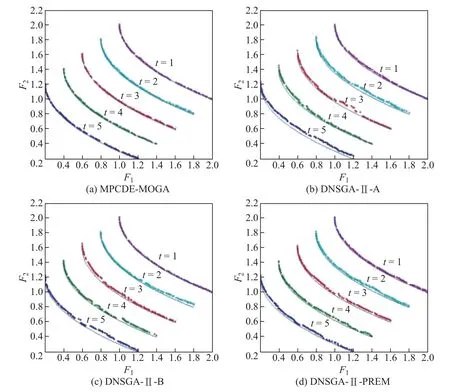
图3 FDA1不同算法Pareto最优解集Fig.3 Pareto optimal solution sets of different algorithms for FDA1

与FDA1不同,DMOP2问题是为了测试算法是否能够找到多样性优良的POF.MPCEDMOGA的收敛性能明显优于其他3种算法,且其分布性也比其他算法好一些,这是由于采用多种群进化策略增加了解的多样性.图4显示了不同算法对于DMOP2的最优前沿与其真实POF的对比情况.为了能更清晰地对比结果,亦采用(F1+t/5,F2+t/5)的方法对不同时刻的最优前沿进行平移,同样MPCED-MOGA得到的结果更靠近真实的问题POF.

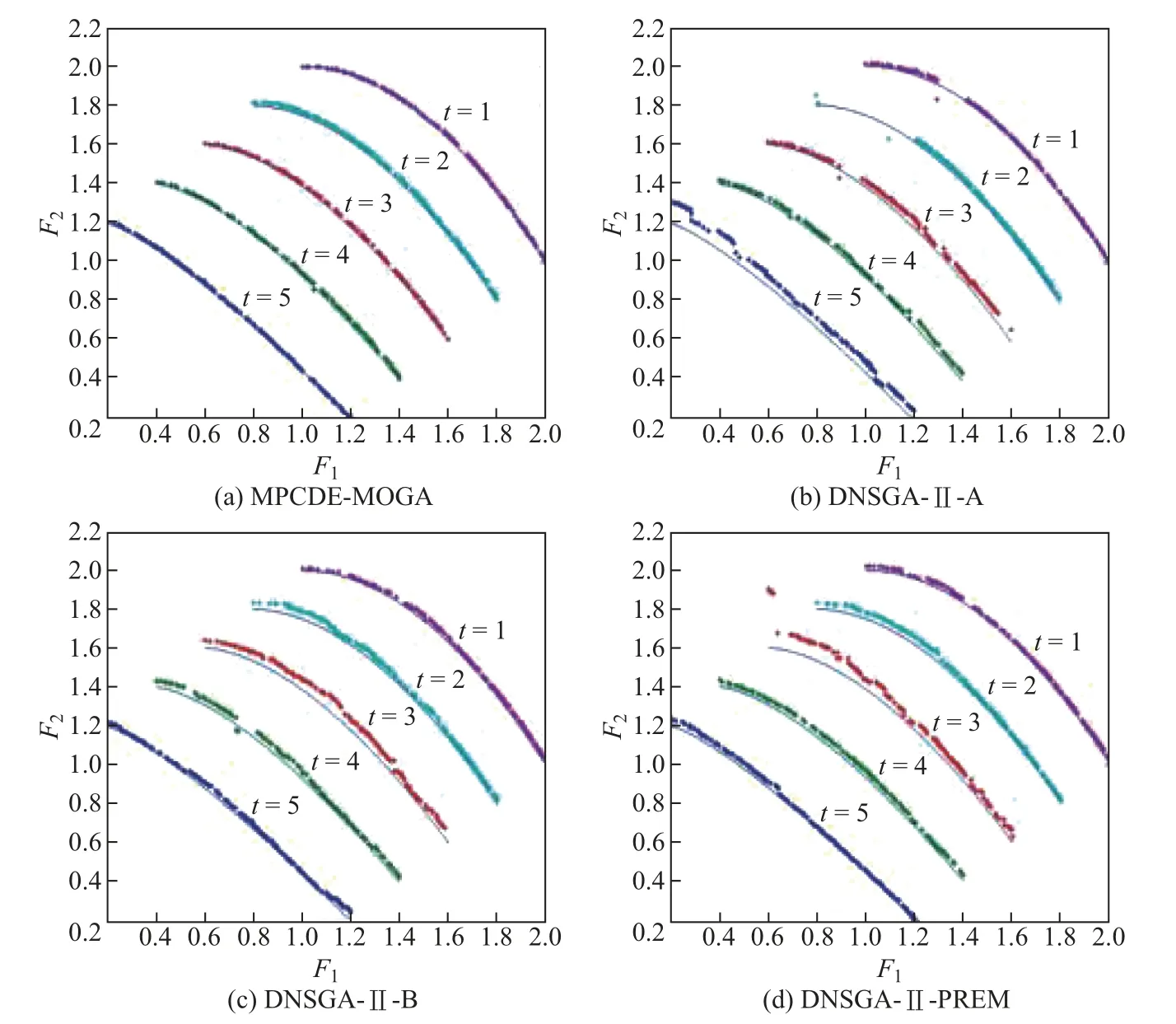
图4 DMOP2不同算法Pareto最优解集Fig.4 Pareto optimal solution sets of different algorithms for DMOP2

对于FDA3函数,FDA3的最优解的某些分量是随着环境(时间)发生改变的,同时其真实POF也随着环境(时间)改变,解的密度也随环境(时间)变化.该测试问题考验算法在搜索最优解的同时,跟踪最优前沿变化的能力,因此对算法的分布性能要求较高.从表1可以明显看出,MPCED-MOGA的收敛性最佳,且分布性能也表现不俗.图5给出了不同算法对FDA3的最优前沿与其真实POF对比情况.从表5可见,在收敛性能和分布性能方面,MPCED-MOGA都明显优于其他算法.

在评价一个多目标算法的过程中,算法复杂度决定了算法的执行效能.在MPCEDMOGA中,时间开销主要由步骤2对2个种群进行遗传、变异操作,对2个种群进行非劣排序,排序算法最坏情况下的时间复杂度为O(mnlogn),计算个体聚集距离的时间为O(mn).因此,步骤2的复杂度为O(mnlogn)+O(mn).单一种群总的算法复杂度为O(mnlogn).考虑到本工作存在搜索种群和跟踪种群这2个种群,算法的时间复杂度为O(m(n1+n2)log(n1+n2)),其中m为目标数,n1为跟踪种群个体数目,n2为搜索个体数目.

3.2 混合交通流信号配时多目标优化仿真分析

3.2.1 相邻交叉口基本信息

本工作以上海天目西路为交通主干道,进行相邻信号动态配时分析.2个交叉口相邻仅230 m,高峰期交通负荷大.采用定周期4相位机制行信号控制,公共周期时长为126 s,不考虑进口道坡度影响.2个交叉口采用同周期相同信号配时方案,各相位黄灯信号时长同为3 s.通过实地调查获得2个交叉口在一周内的早高峰期的交通流数据,此相邻交叉口外进口道的机动车交通流数据[18]和内进口交通流数据由外进口道进入内进口道的流量决定.表3给出了此相邻交叉口非机动车和行人流量数据.

图5 FDA3不同算法Pareto最优解集Fig.5 Pareto optimal solution sets of different algorithms for FDA3

表3 相邻交叉口非机动车及行人流量数据Table 3 Non motor vehicle and pedestrian flow data at adjacent intersections

3.2.2 算法运算结果分析

根据3.4节中提出的相邻交叉口动态多目标优化配时模型,采用本工作提出的MPCEDMOP算法对其进行求解,确定相邻交叉口的最优协调优化控制方案.这里,MPCED-MOGA算法搜索种群规模为100,跟踪种群的规模为50,单个时间窗最大迭代次数取100,其他参数同4.1.

(1)优化目标间的冲突关系分析.

图6为3个目标Pareto解集两两间对比的结果.图6(a)中,随着机动车延误的减小,行人过街等待时间随之增加,2个优化目标相互冲突;从(b)中可以看到,机动车延误与非机动车延误也是相互冲突的目标;(c)表明,对于相邻交叉口而言,非机动车延误与行人过街等待时间表现出近似的线性关系,表明二者之间不具有冲突性.

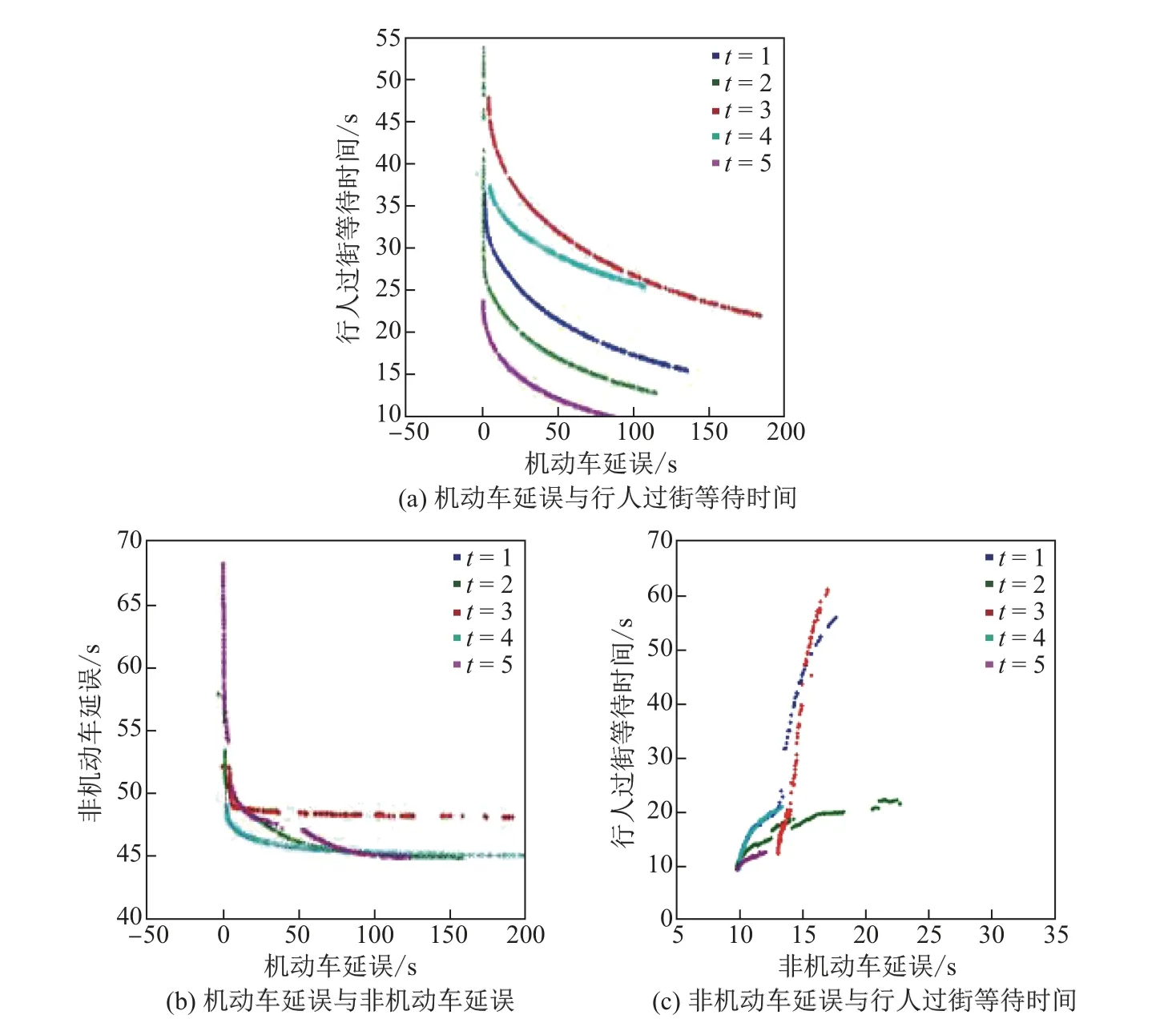
图6 各个性能指标的Pareto前沿Fig.6 Pareto fronts of each performance index

(2)配时方案决策及对比

利用Topsis决策方法[19],从MPCED-MOGA得到的候选配时方案集中选出最满意配时方案,并分别与其他3个算法(DNSGA-Ⅱ-A、DNSGA-Ⅱ-B和DNSGA-Ⅱ-PREM)的结果进行比较.表4给出了不同算法在不同的时间窗下得出的最优方案所对应的性能指标.从表4可以看出,相对于其他算法,MPCED-MOGA优化了决策方案,机动车平均延误、非机动车平均延误、行人过街等待时间这3项指标都有不同程度的降低,即减少了各种交通流滞留在交叉口处的时间.

(3)Matlab与Vissim仿真平台结果分析.

首先,在Vissim平台上搭建在混合交通环境下相邻交叉口路网,本工作建立了相邻交叉口Vissim、Matlab集成仿真平台.

为了验证本工作提出的相邻交叉口实时协调控制的优化效果,首先对比基于不同算法的动态控制方法的控制效果.当2个交叉口流量变化值大于150 pcu/h时,认定交通状态发生了变化,此时启用动态多目标优化算法优化出实时最优配时方案.为清楚地表达仿真结果,设置仿真时长为2.5 h.通过比较交叉口车辆平均延误时间、停车次数以及行人过街等待时间来证明本算法的先进性.

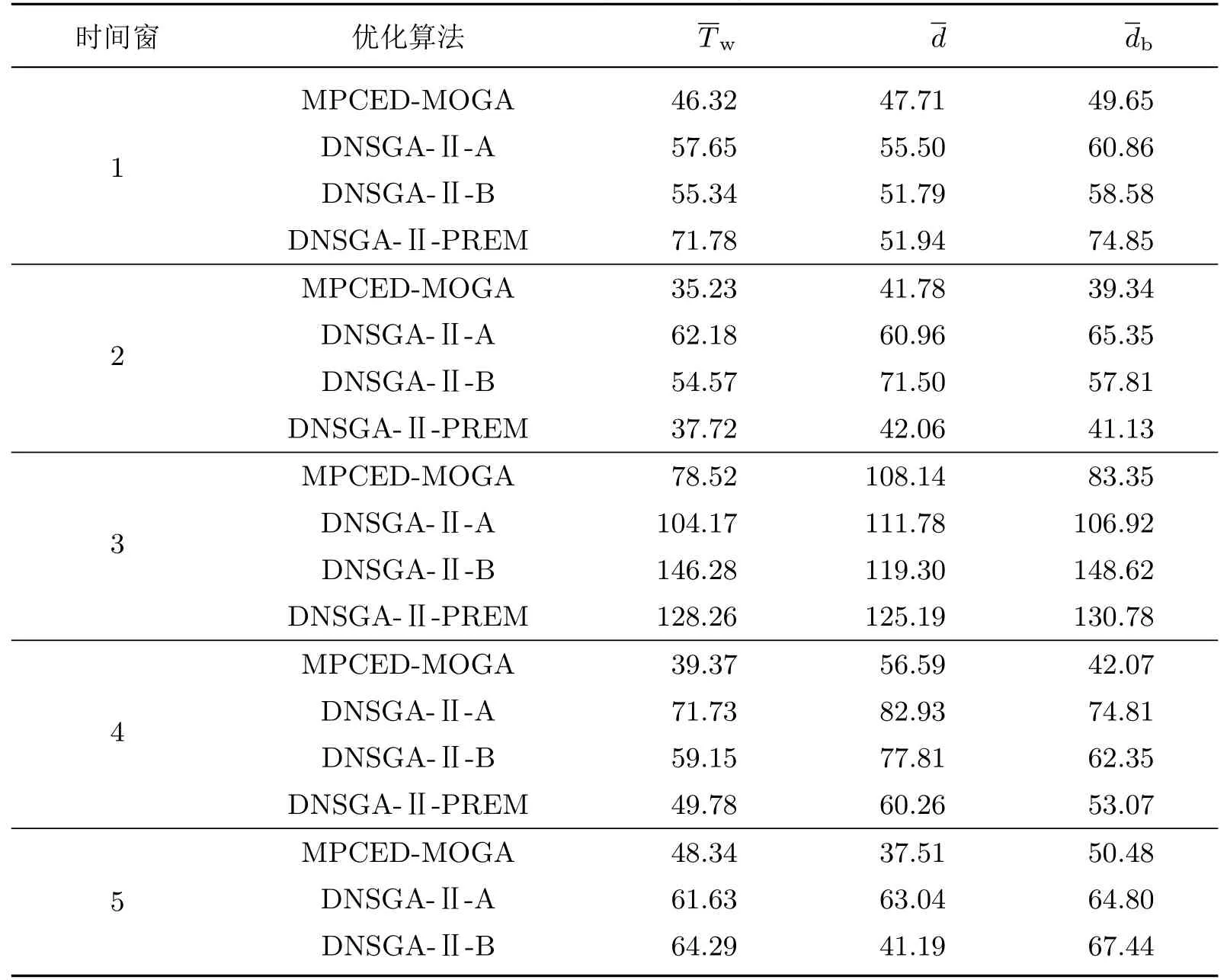
表4 相邻交叉口优化配时方案对比结果Table 4 Comparison results of signal timing at adjacent intersections

表5给出了基于不同算法的信号配时方法的配时效果对比.从表中可以看出,与DNSGA-Ⅱ-PREM算法相比,本工作提出的MPCED-MOGA算法得到的配时方案中,机动车和非机动车停车次数较多,但是机动车延误降低了3.8%,行人等待时间减少了2.6%.同时,表5也对比了本算法和Wester[20]提出的单点配时方法TRRL算法.从表5也可以看出,在本算法下机动车延误降低了34.5%,非机动车降低了25.9%,行人等待时间减少了30.7%,机动车和非机动车的停车次数也分别减少了42.4%和21.8%,提高了交叉口的服务水平.

表5 相邻交叉口不同算法配时效果对比Table 5 Signal timing comparison results of different algorithms at adjacent intersections

4 结束语

针对考虑机动车、非机动车、行人的混合交通流的拥堵状况,本工作根据机动车、非机动车、行人三者的滞留时间均最短为目标,建立了动态多目标优化配时模型;设计了一种基于NSGA-Ⅱ的MPCED-MOGA算法,该算法能更好地解决动态多目标优化问题,与DNSGA-Ⅱ-A、DNSGA-Ⅱ-B、DNSGA-Ⅱ-PREM算法相比,MPCED-MOGA算法的收敛性能和分布性能均更好,且计算时间更短.从仿真实验也可以看出,MPCED-MOGA算法对于机动车、非机动车、行人这3个目标建立的模型,能够更好地求解,并保留解的多样性,从而缩短交叉口的延误时间,提高了道路的通行效率.