PSAT应用于风电系统暂态稳定性研究

辛文成，姚森敬，陈浩敏，于力，席禹

（南方电网数字电网研究院有限公司，广州510663）

随着化石能源等传统能源的日益减少，风力发电作为一种新能源发电技术迅速崛起。然而，随着风电装机容量在电网总装机容量的比重不断提高，风力发电对电网的稳定性带来严重考验。不同类型的风电机组对电网暂态稳定性的影响不同，为了深入地了解各风力发电机组特性以及不同风机对电力系统暂态稳定性影响程度，对风力发电系统进行仿真分析是十分必要的。风电系统的暂态稳定性研究这一课题已被很多科研工作者和电网工作人员青睐，他们也做出了一定的成果。但是对这一课题的研究大都是针对单一类型风机的发电系统，本文将双馈发电系统、直驱发电系统、恒速恒频发电系统对比进行研究，得出了相关结论。另外本文所用的电力系统仿真软件PSAT是近年兴起的电力系统仿真软件，具有小信号稳定分析和时域仿真、潮流计算、连续潮流计算、最优潮流求解等模块，为用户进行电力系统仿真提供了极大的便利。

1 PSAT软件简介

PSAT 是一种新的电力系统分析软件，其命令行版本也是GNU Octave 兼容的。它的核心是潮流计算，会对状态变量进行初始化处理。一旦求出了系统潮流，就能执行后续的静态或动态分析。PSAT 包含计算模块有：小信号稳定分析和时域仿真、潮流计算、连续潮流计算、最优潮流求解等等。

PSAT 具有良好的适用于电力系统仿真的界面，和普通交互界面一样，由菜单栏、状态栏、控件栏等组件。在进行电力系统计算时，在Data file 文本框输入原始计算数据，在Perturbation file 栏录入动态更细数据，在Command line 写入命令以便执行。计算边界条件实时显示在主界面右端，包括计算基准容量、频率、仿真开始及结束时间，收敛门槛等。实时计算结果包括潮流计算结果、最优潮流结果，收敛结果等显示在主界面的右边。

2 电力网络元件的数学模型

风速的模型在很多文献已有详细讨论，这里不作介绍，只介绍各风力机组的和相关换流器数学模型。

2.1 双馈风力发电系统

双馈风力发电系统结构图如图1所示。

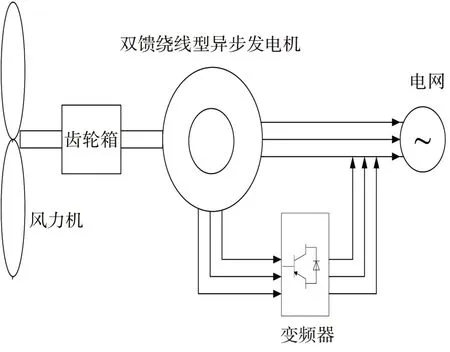
图1 双馈风力发电系统结构图Fig. 1 Double-fed wind power system

为了更好分析问题得出结论，在分析双馈风力发电系统前须作出以下假设：

（1）三相绕组在空间上以120°角对称分布，产生的磁动势以正弦波形式沿圆周分布；（2）各定子绕组转子绕组自感和互感线性对称，不考虑磁饱和；（3）转子绕组阻抗已换算到定子绕组侧，换算完成后，每相匝数相同；（4）不考虑铁芯损耗，绕组电阻不受温度和频率变化的影响。

作出以上假设后，就可以在同步旋转坐标系（-）下建立双馈风力发电机的数学模型，双馈风机的数学模型在很多资料中都有介绍，这里引用中的模型，其中定子侧采用发电机惯例，转子侧采用电动机惯例。

电压方程如下：

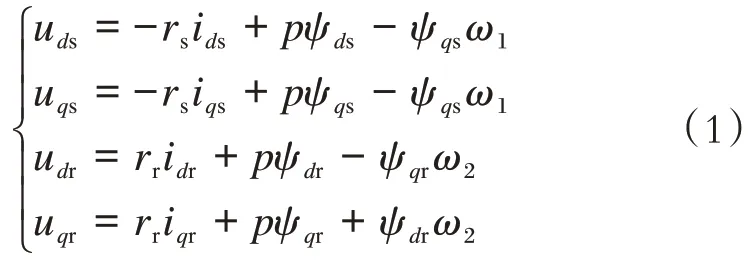
磁链方程如下：

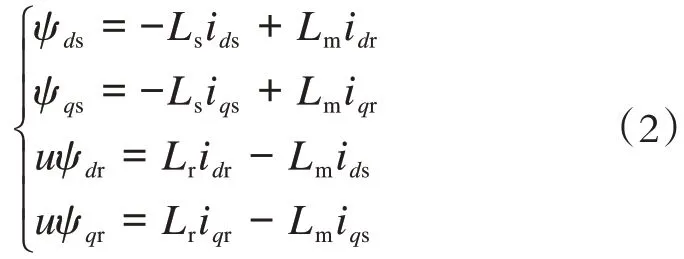
式中：、为定、转子每相电阻（Ω）；、、为定、转子等效电感和互感（H）；i、i、i、i分别为定子-轴和转子-轴电流（A）；为同步转速（r/min）。

换流器的存在使得双馈风力机组的机械部分与电气部分被解耦，本论文的换流器模型没有分为定子侧换流器和转子侧换流器来分别介绍，只是把换流器看成一个整体，与发电机电磁暂态过程相比，换流器的动态过程快很多，因此，换流器可以用一个理想电流原来代替。如文献［7］介绍。将转子电流按-轴分解为i和i，分别用于控制转速模块与电压模块，用方程描述如下：

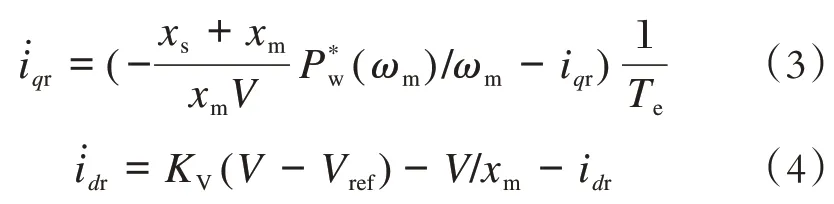
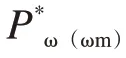
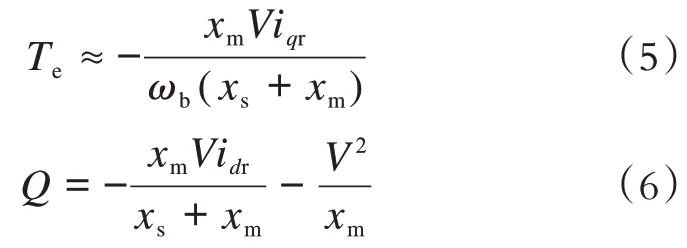
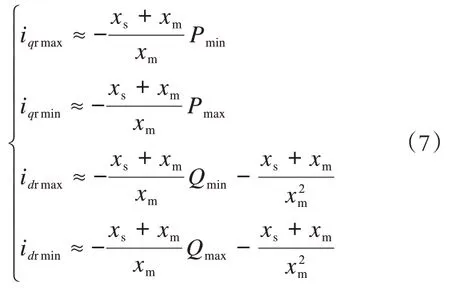
由于电磁转矩和有功密切相关，由以上两式可以看出流过换流器的电流i和i与发电机发出的无功和有功正相关。因为换流对流过它的电流有较高的要求，因此可以设定发电机发出的有功和无功的极值来限制i和i的大小，方程如（7），即设置有功无功的最大值和最小值来限制流过换流器的电流。

2.2 直驱同步风力发电系统

直驱同步发电系统见图2。

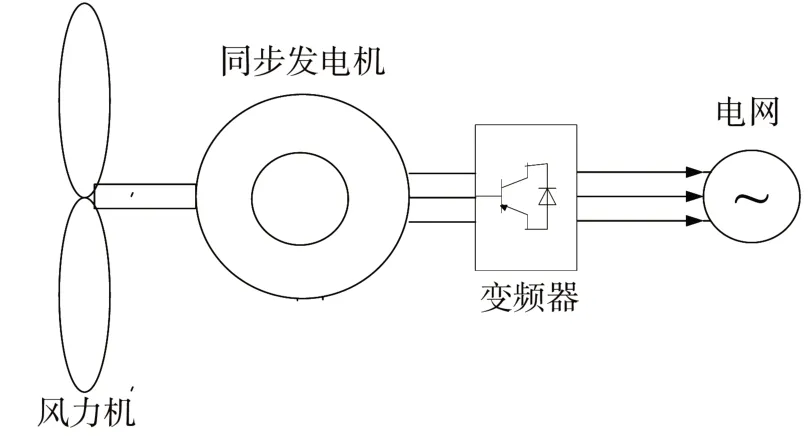
图2 直驱风力发电系统结构图Fig. 2 Direct drive wind power system

在建立同步发电系统方程时，为了计算方便可以假定电机处于电气稳态，因为定子和转子的磁链变化比电网的变化快，因此同步机组的机械部分和电气部分完全解耦。则可以得出如下方程：

电压方程如下：

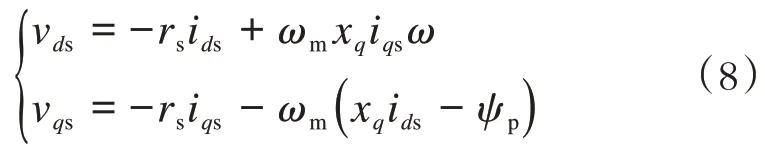
磁动势方程如下：

将换流器看作是理想电源，定子交轴电流i，定子直轴电流i和定子直流电流分量i是状态变量，将他们分别用于转子速度控制，功率控制和电压控制，由于电机速度和电压都有一个限值，因此判断机组是否失稳的标准是看控制电流是否越限。控制电流的限值方程如下所示：

式中：为同步电机的励磁磁动势，其余变量含义和双馈发电系统的一致。

3.3 恒速风力发电系统

恒速风力发电系统如图3所示：

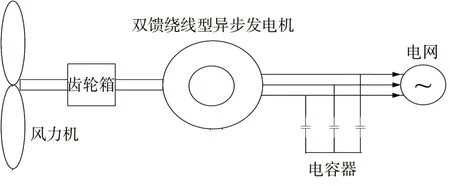
图3 恒速恒频风力发电系统结构图Fig. 3 Constant speed constant frequency wind powersystem

恒速恒频发电系统中元件的模型相对较简单，可以直接在直角坐标系中建立，以网络平衡节点为参考点。可得方程如下：

电压方程如下：

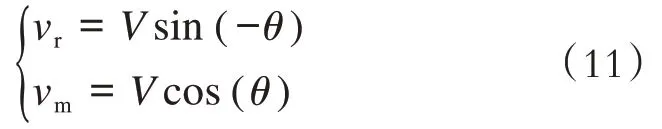
功率方程如下：

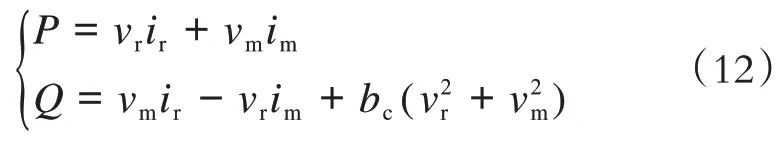
电磁转矩方程如下：

3 算例分析

本论文采用的仿真模型为WSCC 的三机九节点模型，见图4。

图4 是以双馈风机为例，在对其它类型的风电系统进行仿真时，只需将BUS2 上的双馈风机改成其它类型的风机即可。BUS8 处设置的为三相短路故障。论文研究在三相短路故障和甩负荷两种情况下，各风电系统的暂态稳定情况。关于暂态稳定分析的数学原理，即功角方程解法在相关文献［8］中有介绍，本文只给出系统仿真图。

3.1 三相短路故障时风电系统稳定性

在BUS8 处，将短路故障的开始时间设置为1秒，故障持续时间分别为120 ms、246 ms和625 ms。可得出如仿真图5。

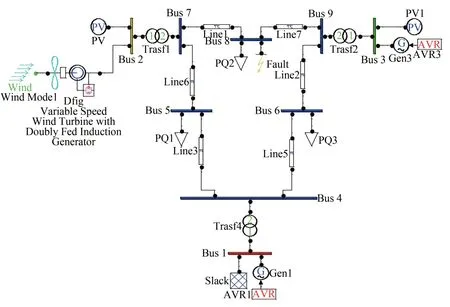
图4 三机九节点系统图Fig. 4 3-genreator 9-node power system

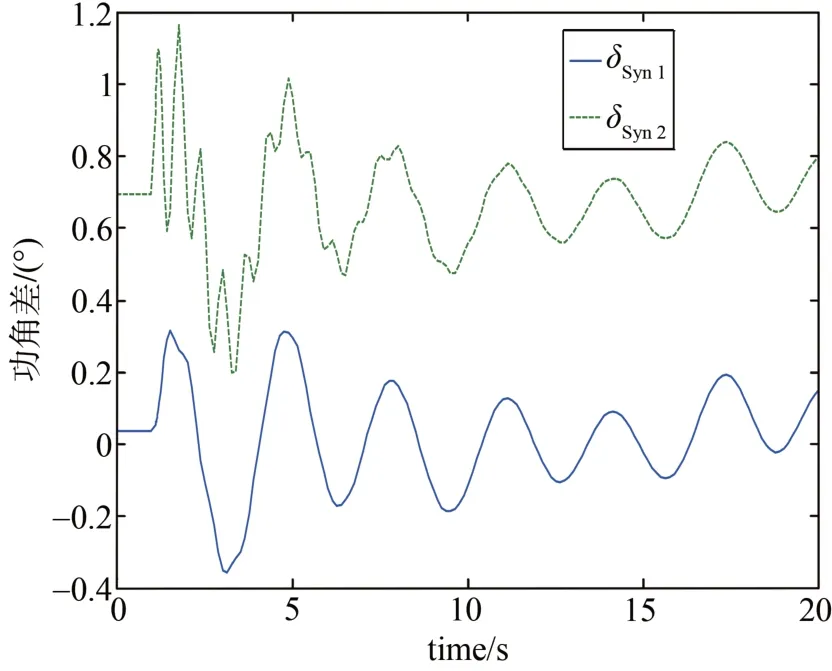
图5 故障持续120 ms时直驱风电系统同步电机的σ-t曲线Fig. 5 The σ-t figure of direct drive wind power system in 120 ms fault duration

从图6 可以看出，在故障开始后，恒速风机的转速急剧变化，但在故障清除后，转速开始回稳，大约在4 s时趋于稳定，即恒速风机本身是稳定的。

当故障持续时间为246 ms时，含双馈风机的电力系统能保持暂态稳定，但转子电流越限，如图7所示，因此机组本身不能保持稳定；含直驱同步电机的电力系统的功角变化是同步的，转子电流不越限，因此它们也都保持稳定；含恒速机组的电力系统保持稳定，但功角比故障前的功角大。

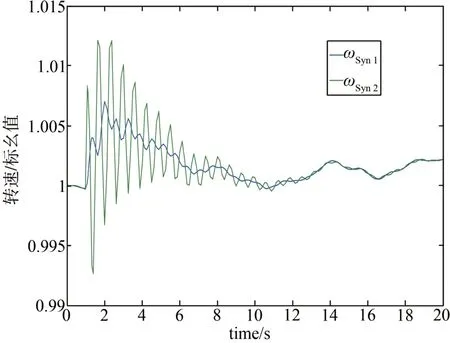
图6 故障持续120 ms时恒速机组的转速曲线Fig. 6 The rotate speed figure of constant speed wind power system in 120 ms fault duration

当故障持续时间为625 ms时，含双馈风机的电力系统仍然能保持稳定，但转速和功角都比原来大很多，已接近不稳定状态，转子电流继续越限，双馈机组本身不能保持稳定；含直驱风机的电力系统不稳定，机组也不稳定，仿真不能完全结束；含恒速风机的风电系统不稳定，恒速机组本身也不稳定，仿真结果不收敛。

通过以上分析，将三种发电系统以及机组本身的暂态稳定性结果填入表1。

同时，为了研究三种风电机组在故障持续时间为625 ms 时的低电压穿越能力，得到BUS7 处电压曲线如图8～图10所示。

图7 故障持续246 ms时双馈风机的转子电流曲线Fig. 7 The rotor current figure of double-fed wind power system in 246 ms fault duration

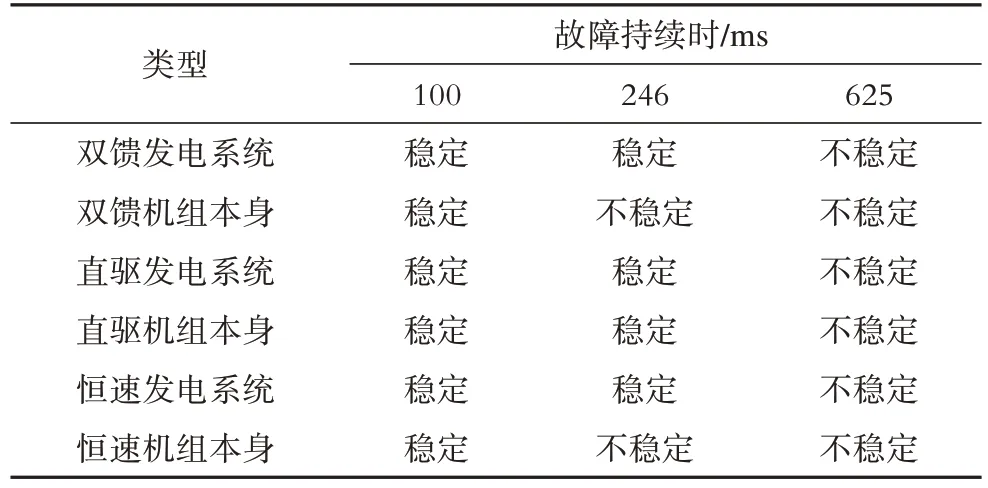
表1 三种风电机组及系统稳定性对比Tab. 1 Contrast of the stability between wind plants

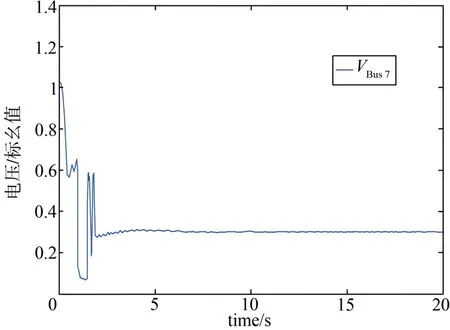
图8 故障持续625 ms时恒速风电系统BUS7处电压Fig. 8 The voltage of BUS7 of constant speed wind power system in 625 ms fault duration

以上图形表明，当故障持续时间为246 ms时可明显看出直驱风机的低电压穿越能力较好，当故障时间达到625 ms时，尽管三种风电机组都有一定的低电压穿越能力，但系统最终仍然失去稳定性。

3.2 系统无功补偿时，各风电系统暂态稳定性

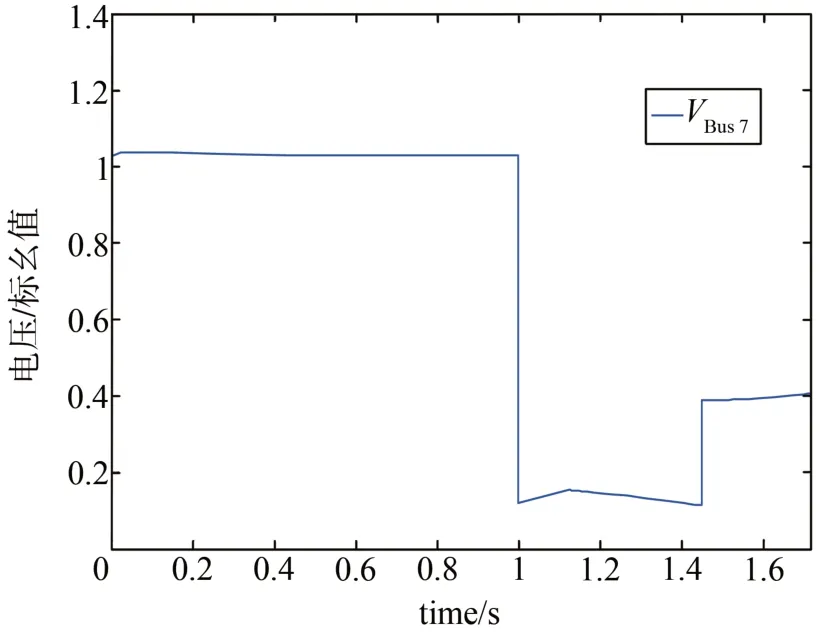
图9 故障持续625 ms时直驱风电系统BUS7处电压Fig. 9 The voltage of BUS7 of direct drive wind power system in 625 ms fault duration

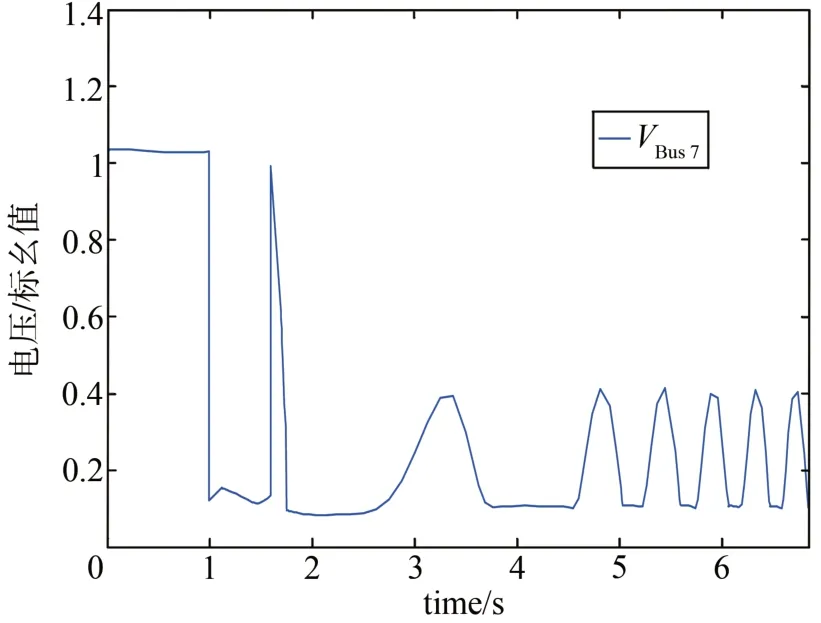
图10 故障持续625 ms时双馈风电系统BUS7处电压Fig. 10 The voltage of BUS7 of double-fed wind power system in 625 ms fault duration

当短路故障持续时间较长后，尽管低电压穿越能力对系统有一定积极作用，但不能使系统恢复稳定。此时，考虑在系统中加入无功补偿，容量取为风机容量的40%，为40 MVar。本算例在故障点BUS8处集中加入静止无功补偿器，仿真图形如图11～图13所示。

由以上图形可看出，SVC 加入对恒速风电系统的作用仍然不明显，但对双馈风电系统和直驱风电系统有较明显作用，使得BUS7 处的电压能较好的恢复。但由后续分析可知，当故障持续时间继续增加时，尽管有无功补偿容量，但上述三种风电系统仍然不能保持稳定。

3.3 负荷急剧变化时，各风电系统暂态稳定性

当无功负荷分别由0.45、0.5和0.45个标幺值减少到0.05、0.05 和0.05 个标幺值，经过仿真后可以看出各风电系统都能保持稳定性，只是系统稳定时的功角和转速与初始值差距比较大，如图14 所示；双馈风机的转子电流越限，即机组本身不稳定，如图15所示。

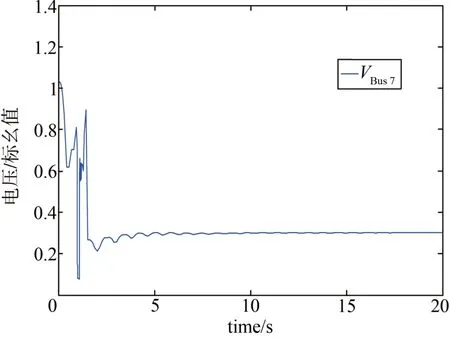
图11 故障持续625 ms加入SVC后恒速风电系统BUS7处电压Fig. 11 The voltage of BUS7 of constant speed wind power system in 625 ms fault duration with SVC

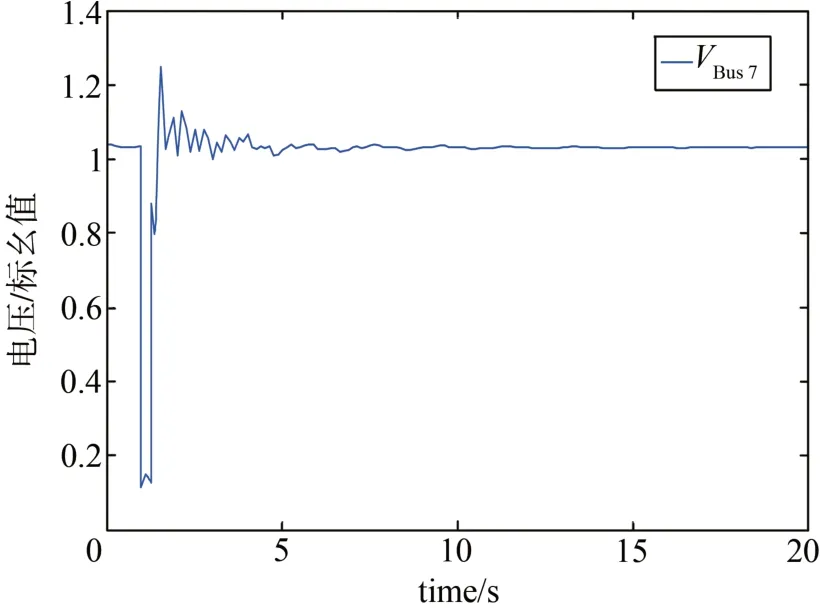
图12 故障持续625 ms加入SVC后直驱风电系统BUS7处电压Fig. 12 The voltage of BUS7 of direct drive wind power system in 625 ms fault duration with SVC

图13 故障持续625 ms加入SVC后双馈风电系统BUS7处电压Fig. 13 The voltage of BUS7 of double-fed wind power system in 625 ms fault duration with SVC

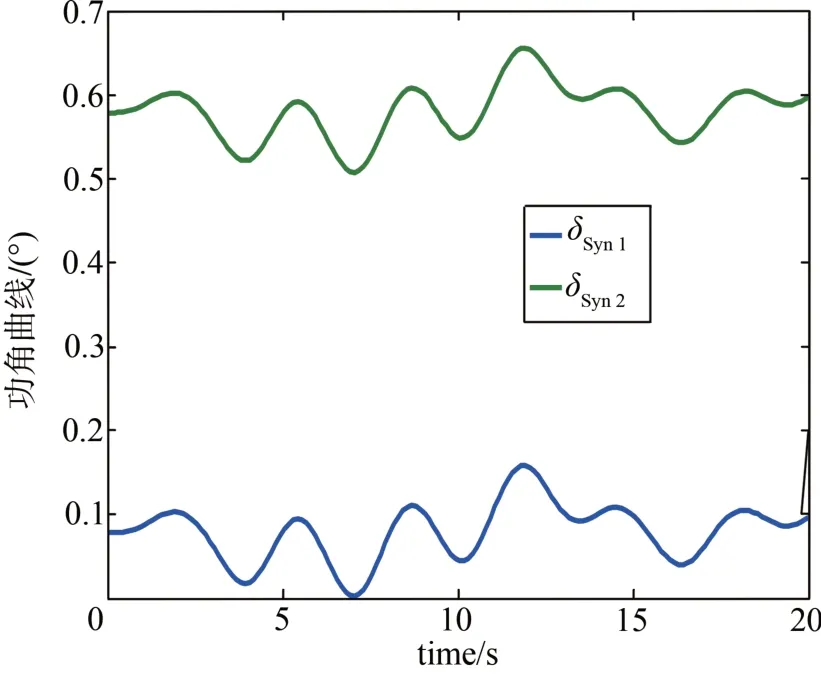
图14 无功负荷减少时电力系统功角曲线Fig. 14 The power angel with reduce of reactive load

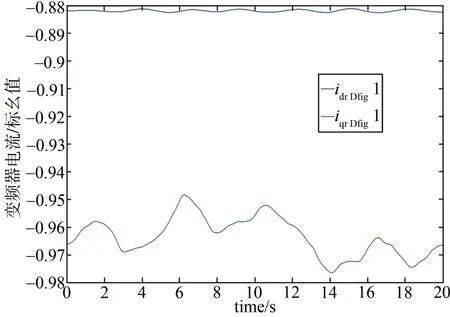
图15 无功负荷减少时双馈风机的转子电流曲线Fig. 15 The rotor current of the double-fed wind power system with reduce of reactive load

在有功负荷减少的过程中，含双馈风机的电力系统由稳定变为不稳定，机组本身也慢慢失稳，直驱风电系统和恒速风电系统也慢慢失稳。如图16描述的是在有功负荷由0.9、0.9和0.9个标幺值减少到0.6、0.6 和0.6 个标幺值时，双馈电力系统电压曲线。

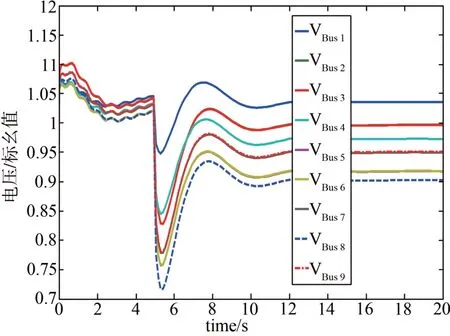
图16 有功负荷减少时系统电压变化Fig. 16 The change of the voltage with reduce of reactive load

4 结论

本文在PSAT 上建立了几种风机的数学模型，并进行了暂态稳定仿真，在比较的基础上得出了如下结论：

1）故障持续时间越长，系统越容易失稳；在短路情况下，双馈机组本身的稳定性较难保持，但系统稳定性保持较好。

2）双馈机组和直驱机组低电压穿越能力要好于恒速机组。

3）无功补偿容量的加入使得双馈风电系统和直驱风电系能较好的恢复稳定，但随着故障时间进一步增加，无功补偿的作用将不会很明显。

4）突然甩负荷对各风电系统的稳定性都有较大的影响。

5）同传统电力系统相比，含双馈风力发电机的电力系统受负荷影响较大，突然甩负荷使得双馈风电系统和机组本身很容易失稳，即双馈系统对负荷变化非常敏感。相对来说直驱风电系统和恒速风电系统的稳定性能较好保持，但机组本身也较容易失稳。

6）由于换流器的解耦作用，双馈风机和直驱风机暂态稳定性受发电机转速影响较小，受换流器电流大小较大的限制。因而变速风机的稳定性与换流器本身的特性有密切关系。