《图形中的规律》两次听课的思考

【摘要】本文简述两位老师执教的《图形中的规律》课堂教学片段，结合调查得到的结果进行分析，提出实现数学课堂“过程与方法”目标的策略，从过程与方法目标的外化实践、重视数学思想方法的培养两个方面，提升数学教学成效。

【关键词】过程 方法 体验 思考 《图形中的规律》

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）33-0110-02

过程与方法是数学课堂教学的三维目标之一。很多教师在备课时对过程与方法进行了预设，但在教学实践中很难有效落实，这就导致了就题论题的现象，使学生知其然却不知其所以然。笔者对同一内容不同教法的过程比较和课后调查发现，教师在教学时对“过程与方法”目标重视与否，会影响学生学习的效率，而达成这一目标的有效策略之一是教给学生探究的方法，并且从注重“过程与方法”目标的外化实践、重视数学思想方法的培养、加强学习过程的体验和内化三个方面去努力。

那么，如何在数学教学中给予学生充分理解感悟的机会，让学生逐步掌握一定的数学方法呢？笔者听了两位教师执教北师大版数学五年级上册《图形中的规律》一节课后，就此问题谈谈个人的思考。

一、案例描述

（一）甲老师的教学片段

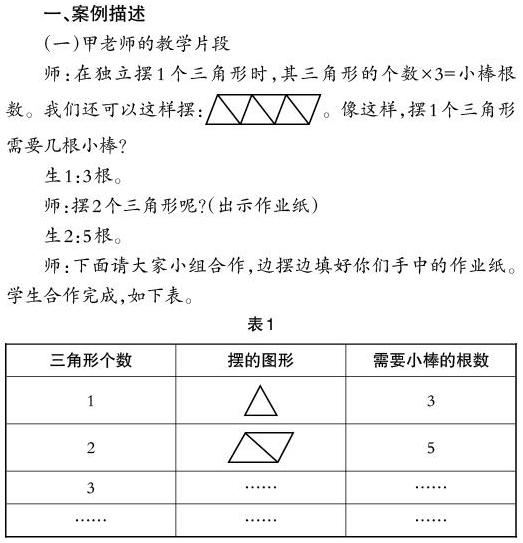
师：在独立摆1个三角形时，其三角形的个数×3=小棒根数。我们还可以这样摆：像这样，摆1个三角形需要几根小棒？

生1：3根。

师：摆2个三角形呢？（出示作业纸）

生2：5根。

师：下面请大家小组合作，边摆边填好你们手中的作业纸。学生合作完成，如下表。

师：观察表格，你发现了什么规律？（学生陷入思考中）

生3：每多摆1个三角形就需要多2根小棒。

师：还有没有其他发现？

生4：我发现小棒的根数是三角形个数的2倍加1。

师：这位同学找到了三角形的个数与小棒之间的关系，你能不能结合图形再找一找规律？

……

师：那么，摆放100个三角形需要几根小棒呢？

生5：201根。

（二）乙老師的教学片段

师：独立摆放三角形时，三角形个数×3=小棒根数，现在我们知道还可以这样摆：<P：＼广西教育＼2021-9A＼图片＼广教第9期30.tif>。猜一猜，摆放100个这样的三角形需要几根小棒？

生1：300根。

生2：不对，肯定比300根要少，我猜大概是270根。

生3：我猜是200根。

……

师：那我们动手试试看吧。

（学生操作，摆放了十几个三角形之后发现桌面摆不下了，有的学生一时不知道该怎么办，有的干脆把旁边的桌子拉过来并在一起继续摆，可是没摆多久又满了）

生4：老师，我摆不下去了。

师：这可怎么办？怎样才能知道摆放100个三角形需要几根小棒呢？

生5：一定是有规律的，我们去找规律！

生6：对！先摆3个、4个、5个，看看各需要几根小棒，就能发现规律了。

师：你们说这里有什么规律？怎样去发现或验证规律呢？

生7：可以多摆几次。

师：万一在摆的时候忘记前面的根数了呢？

生8：那很简单，我只要把每次摆放的情况都记录下来就不会忘记了。

师：你是说用列举的方法把结果记录下来，再来找规律是吧？真好，我们在发现或验证规律时，通常会用到这样的方法。下面就请同学们分小组来试一试，看看到底有没有规律，或者有什么规律。

（学生操作、记录、讨论）

师：哪些小组有了新发现？

（各小组争相发表自己发现的过程和结果）

二、课后调查

甲乙两位教师都给了学生一定的思考空间，让学生“自己得出图形中的规律”，开始关注学生的学习过程，整节课显得生动、热闹。然而，学生在课后对“图形中的规律”到底收获多少呢？对此，笔者对两个班级学生进行课后调查，出示图1，问题如下：

（1）搭4个房子图形需要多少根小棒？

（2）搭100个房子图形需要多少根小棒？

（3）你是怎样发现这个规律的？

调查结果如下表2。

从上表2不难发现，两个班级的学生在回答第（1）题时差异并不明显。但是在寻找规律、提炼规律、应用规律上，乙老师班级的学生明显会自己选择策略进行有序探索，呈现出从简单例子找规律、从直观图中找规律、从猜想验证找规律等不同的策略，规律的归纳也有“5+99×4，1+100×4，2×100+2×100+1”等多样化的模型。可见，乙老师班级的学生对规律的探究更加有法有序、高效多样。

为什么会出现这样的教学效果呢？笔者对比发现，甲乙两位教师执教的两节课都体现了动手操作、实验探究等学习方式，学生摆得开心、学得投入。相比之下，甲老师的课虽然让学生按照一定的方法找到了规律，但学生对这些方法体验并不深，其目标定位还停留在得出图形中的规律，重在“规律”的结果;而乙教师的课更注重学生对学习方法的讨论和体验探索的过程，教师关键性的引导语有“你们说这里有什么规律”“那要怎样去发现或验证规律呢”等，学生体会并获得探究规律的过程与方法。这样的教学，让学生在找规律的任务驱动下调动所有的感官参与，特别是思维参与，在亲身经历中体会到了找图形规律的必要性、学习了找规律的一般方法及经历了提炼规律的过程。教师把探究空间留给学生，目的是让学生亲身经历探索的过程，把“如何探索归纳出图形中的规律”作为核心目标再落实。

三、听课反思

细细剖析两节课，可以发现两位教师最大的不同在于教学追求上，甲教师主要教给了学生“图形中的规律”，乙教师主要教给了学生“如何找到图形中的规律”。显然，从学生的发展角度而言，教师教给其方法要比教给结果有价值得多。而之后的调查更是给了笔者很深的感触，在实际教学中，教给学生单纯的知识是不够的，还应该教给学生探究数学的方法，也就是授予学生真正意义上的“渔”。要做到这点，笔者认为最关键的是做到以下两个方面：

（一）数学课堂应注重“过程与方法”目标的外化实践

理解并掌握一定的思考方法，关键在于学习的过程。那么，如何在课堂教学中体现过程与方法目标，如何将过程与方法目标外化为教学实践呢？我们需要多做出一些案例分析和课后反思。很多教师有了这个意识，也去实践了，但在具体实施过程中总是容易偏离目标轨道。

在《图形中的规律》教学中，规律的寻找其实只是一个任务，这个规律只能在这一道题中得以应用。但是，寻找规律的过程可以让学生积累数学活动经验、体会发现规律的思考方法、感悟直观模型与抽象表征的相互转化。这有助于培养学生的数学思维能力，在遇到新问题时能主动激活思维，有意识地运用一定的方法去发现隐含着的规律。由此可见，教师在具体实践操作中应当长期关注“过程与方法”的目标，并寻找行之有效的教学策略，促进该目标的落实。

（二）数学课堂应注重教给学生数学思想方法

“找规律”的内容贯穿整个小学阶段，从低年段简单地寻找数字之间的规律，如：2，4，6，8，（  ）等;到中年段寻找简单图形中的规律;再到高年段找更复杂的数形规律，如：一条线段能把一个长方形分成两部分，4条线段最多能把一个长方形分成几部分？n条线段呢？这些内容看似出现在不同的年段，方式也各不相同，但从根本上而言，其思维方式异曲同工。这值得教师思考如何在“找规律”的过程中，逐步教给学生数学思想方法，如果哪些思想方法是可以贯通的，就不要重复教;不同的阶段有哪些思想方法需要强化，在教学时就要有所侧重。教师不仅要让学生真正理解找规律的必要性，而且使他们自主掌握找规律的一般方法。

对《图形中的规律》一课的分析讨论只是一个引子，数学课应该避免只教知识、不重方法。当学生真正转变意识，在操作中开始行动，把达成过程与方法的目标作为行动准则时，他们的数学思维能力就能得到有效的培养。久而久之，学生的视野更加开阔，他们的思维也更加灵活。

总之，小学阶段是学生学习抽象数学思维的关键时期，需要教师注重培养学生的数学思维能力。教师在小学数学课堂中需要给足学生主动探究的空间，让学生充分经历猜测、试验、列举、观察、归纳、推理等学习过程，逐步提升数学学习成效。

【作者简介】葛敏辉（1982— ），男，浙江东阳人，大学本科学历，高级教师，现就职于浙江省金华东阳市吴宁第五小学，主要从事小学数学教学与研究。

（责编 楊 春）