磁脉冲压缩电路的仿真分析

杨银辉，郑义军，谭荣清，李庆轩

(1.中国科学院 空天信息创新研究院，北京 100094;2.中国科学院大学 电子电气与通信工程学院，北京 100049;3.中国电子科技集团公司 光电研究院，天津 300308)

引 言

近年来,随着激光技术的发展与成熟，激光的应用领域也越来越广泛，同时对于激光器的要求也在不断的提升，其中比较重要的几个因素为激光器的寿命、体积和重复频率。以横向激励大气压二氧化碳激光器为例，影响其寿命的主要因素是其放电开关，传统常用的放电开关主要以气体放电开关为主，其开关速度快,但工作寿命偏短。1968年，PERKINS从磁性材料的磁滞回线B-H(其中，B是磁感应强度，H是磁场强度)这一的特征参量出发，对磁开关(magnetic switch,MS)进行了理论上的分析，自此奠定了磁开关的理论基础[1]。20世纪80年代起，以磁开关为代表的固态开关开始被用于脉冲功率技术领域[2]，进一步提升了开关的效率，降低了开关的损耗，延长了开关的寿命，磁开关极其有望成为替换气体放电开关的关键器件[3]。同时磁开关脉冲的重复频率的进一步提升，也大大提高了脉冲形成单元的性能[4-6]。近年来随着磁芯材料制造工艺的不断成熟，磁开关的体积也越来越小更加适合应用于气体激光器中，而磁开关的效率及其运行时的稳定性对于激光器向更高频率的发展有着很大的影响，磁开关的稳定性对于激光器的正常运行来说更是至关重要。

因此,本文中结合PSPICE仿真软件[7-8]从理论上分析了影响磁开关效率及其稳定性的主要因素,并且采用控制变量法逐一分析了复位电流、负载电阻对于磁开关效率的影响，分析了复位电路对于电路稳定性的影响，并且最终以纳米晶磁芯为例进行仿真，取得了最优的复位电流的大小以及负载电阻的大小。

1 磁脉冲压缩电路的工作原理及总体积的计算

磁脉冲压缩电路中的关键器件为磁开关，而磁开关设计的核心是软磁材料的磁感应强度变化的特性[9-10]。可以将磁开关比作一个会随着电压变化的电感，当磁开关两端的电压值没有达到其饱和值时，其电感值很大，相当于断路。当磁开关达到饱和时，其相当于很小的电感，比作一个开关的话相当于闭合状态。正常工作时磁开关通过两种状态之间的转换，结合储能元件储存的能量可以在更短时间内得到释放，从而达到脉冲压缩的目的[11-14]。在磁场中，软磁材料中的磁感应强度与磁场强度的关系可以用磁滞回线[15-16]表示，如图1所示。图1中曲线上每个点的斜率表示磁芯的磁导率即μ=dB/dH。磁滞回线所包围的面积表示经历一个周期过程后铁磁体损耗的能量，面积越小损耗越小。

Fig.1 Hysteresis loop

如图1所示,磁滞回线上的点Bs和Br表示为饱和磁感应强度和剩余磁感应强度，Hc和Hs表示矫顽磁场强度和饱和时的磁场强度，ΔB表示磁通量变化量的最大值。从图1中可以看出,磁场强度大于Hs后，即磁开关饱和以后，磁导率急剧减小，因此实现了磁开关从高感抗到低感抗的跳变。设计时磁芯两端的电压需要满足伏秒积平衡方程式：

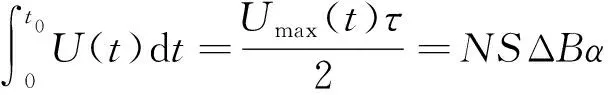
(1)

式中,Umax(t)为磁开关两端所加的最大电压值，τ为磁芯达到饱和所需要的时间，α为磁芯叠片系数，N为磁芯绕组匝数，S为磁开关磁芯有效截面积。根据(1)式可知，磁开关达到饱和所需要的时间τ与磁开关两端的电压最大值Umax，磁芯绕组匝数N，磁芯有效横截面积S，磁通密度变化量ΔB以及磁芯的叠片系数α有关。在进行实验仿真之前,经对相关文献的调研，仿真所用磁芯为纳米晶磁芯，在磁芯确定之后，其磁通密度变化量的最大值ΔB也就为确定的值。

图2所示为典型多级磁脉冲压缩电路的原理图。其中C0为初始储能电容，C1～Cn为中储电容，R为无感电阻。开关J闭合后，能量从C0经L0对C1进行充电，在能量刚好完全谐振传输到C1时，磁开关MS1刚好达到饱和状态，设计时饱和时MS1的电感远小于L0,从而保证能量可以传输至C2，当能量从C1完全传输至C2时，MS2刚好达到饱和，从而继续往后级传递，后级饱和时的电感都要小于前级饱和时的电感，这样才能保证能量逐级往后传递，同时达到脉冲压缩的目的。根据参考文献[17]可知，在各中储电容容值相等时传输效率最大，因此设置时使各级电容容值均相等。以第n级磁开关MSn为例进行分析，当磁开关MSn达到饱和导通时其对后级谐振的传输时间为:

Fig.2 Schematic diagram of multistage magnetic pulse compression circuit

(2)

式中,Ln为饱和时的电感值，其值为:

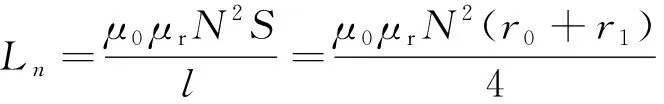
(3)

式中，μ0为真空中磁导率，μr为饱和时相对磁导率，r0为磁芯的内半径，r1为磁芯的外半径。

单级压缩比及总压缩比为可以表示为:

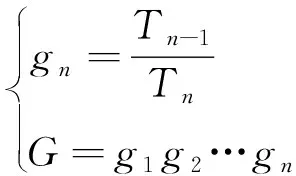
(4)

第n级磁芯体积可以表示为[18]:

(5)

式中,V0为理想状态下的磁芯体积，γ为传递系数，β为填充系数，μsat为磁芯饱和时磁导率，E为脉冲传输总能量。由上式可知,在磁芯类型确定后，理想状态下体积只与E和gn有关，结合(4)式和(5)式可知，磁脉冲压缩电路的总体积可以表示为：

(6)

由(6)式可知，磁芯总体积为压缩比与压缩级数的函数，在总压缩比一定及各级磁芯大小相同的前提下，对于任意的压缩级数当各级压缩比相同时其总体积可以获得理论最小值，可根据伏秒积平衡方程式推出磁芯的半径大小。但是在实际电路中当压缩级数增加，相应的中储电容以及复位电路等都在增加，复位电路和电容的体积不可忽略，级数增加后在其上的损耗也将会明显增加。因此在实际的电路中可以适当地减少压缩级数，根据实际情况计算实际的体积与效率。通常情况磁脉冲的压缩级数不会超过4级。对于应用到激光器的脉冲来说一般需要从几微秒量级压缩到几十纳秒量级，所以压缩比在一百左右，仿真中以总压缩比为100，采用两级压缩进行仿真分析以取得该情况下最大效率。

2 磁芯建模及磁滞回线的仿真

非线性磁芯的建模利用PSPICE中的模型编辑器，使用模型编辑器可以对磁芯的B-H线进行相应的修改和调整，从而得到所需的磁芯。然后根据参量提取得到Jiles-Atherton模型参量，最后进行磁芯型号的选择。目前常用的磁芯材料[19]有硅钢片、软磁铁氧体、坡莫合金、非晶合金以及纳米晶合金。其中硅钢片具有较高饱和磁感应强度，但是其矫顽力较大、电阻率较低，高频下损耗急剧增加，且磁导率较低。软磁铁氧体具有较高的电阻率、高频损耗较小，但其矫顽力较大，磁导率较低，饱和磁感应强度较低。坡莫合金初始磁导率较高，矫顽力较小，但其饱和磁感应强度不够高，电阻率较低，且在频率大于20kHz时，损耗较大。非晶合金与纳米晶合金都具有较高的饱和磁感应强度，较低的矫顽力，电阻率相对其它金属磁性材料较高，并且最大磁导率较高，损耗较低，综合性能较好。因此可饱和变压器磁芯选择为铁基非晶合金，磁开关所用磁芯材料为纳米晶合金磁芯。

下面以厂家提供的实际纳米晶磁芯的磁滞回线为准，对磁芯进行建模和参量提取。实际纳米晶磁芯磁滞回线如图3所示，其中横轴单位为Oe，纵轴单位为Gs。

Fig.3 Hysteresis loops of actual nanocrystalline magnetic cores

(1)首先打开模型编辑器并选择File-New，新建并进行保存，然后选择Model-New新建磁芯模型，对其进行命名然后选择Magnetic Core，单击OK后进入如图4所示界面。

Fig.4 Model editor interface

(2)在如图4中的Initial Permeability中输入初始磁导率100000。

(3)进行坐标设置。

(4)对Jiles-Atherton进行参量提取，各参量取值如表1所示。

Table 1 Magnetic switch core model parameters table

后续的仿真将会在此基础上对磁滞回线的横截面积及平均磁路长度做相应调整以取得体积最小值。图5为各参量确定后得到的磁滞回线。采用试错法对所建立的磁芯模型进行检验后符合要求。

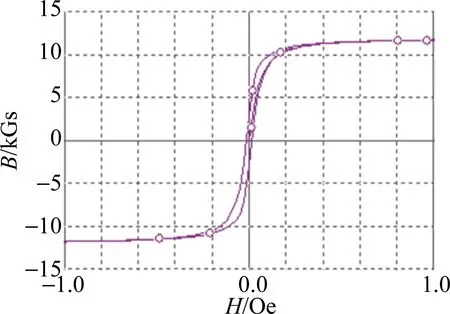
Fig.5 Hysteresis loops obtained by modeling

3 磁脉冲压缩电路的仿真

根据如图6所示的磁脉冲压缩电路原理图使用PSPICE搭建电路进行仿真分析。设计中脉冲变压器及两级磁开关所用磁芯的具体参量如表2所示。按照上述磁芯模型的建立步骤分别设计好脉冲变压器磁芯模型以及磁开关的磁芯模型。在对电路中电容值进行计算首先设置电容C0=4μF，根据能量守恒定律可计算出电容C1=10nF，因此将C2和C3均设置为10nF。

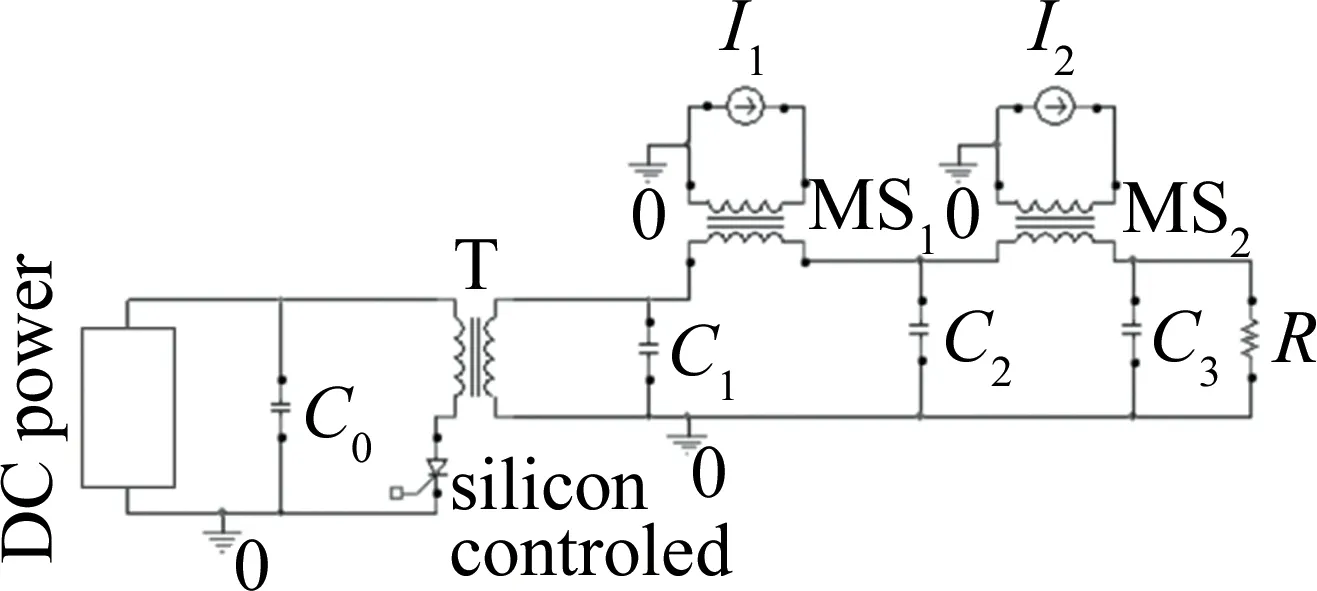
Fig.6 Schematic diagram of magnetic pulse compression circuit

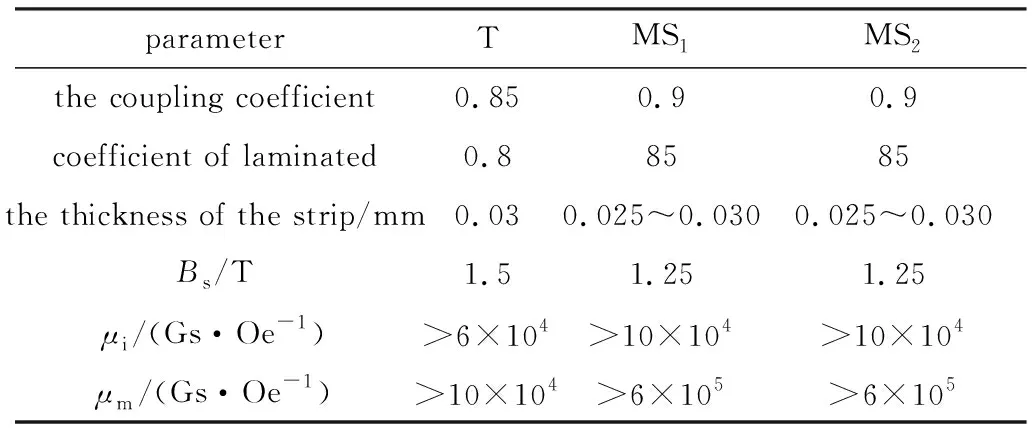
Table 2 Pulse transformer and magnetic switch core parameters

T为可饱和升压变压器，MS1和MS2为一级和二级磁压缩开关，其中直流电源为可调节直流电源。控制开关选用的是可控硅控制开关，其具有体积小、效率高、稳定性好、工作可靠等优点，实验中可通过控制可控硅的开启和关断控制电路脉冲的产生，其控制频率为输出脉冲的频率。

在各参量均设定完成后，为增加磁开关在工作时的稳定性，以及在重频条件下使磁开关能够快速恢复到初始状态，设计中给磁开关添加了复位电路。采用的复位方法是外加直流电流源，复位电路中流过复位绕组的直流电流可以提供一个反向磁场，使磁芯的工作点可以回到初始的负向饱和区域。由参考文献[10]可知，为了使磁芯进入深度的反向饱和区复位电流I必须大于此值，即：

(7)

式中,ra为磁芯平均半径，Hs是负向饱和时的磁场强度，Nr是复位端的绕组匝数。由图4中的磁滞回线可知，在磁场强度大于24A/m时磁芯开始饱和，结合上述公式可以计算出，在一级复位绕组为9匝时磁开关复位电流理论最小值为I1=1.09A。在二级复位绕组为3匝时磁开关复位电流理论最小值为I2=3.27A。负载电阻初始设定值为200Ω，在PSPICE中将两个复位电流设置好后对整体电路进行仿真，并将探针放置在电容C1，C2，C3高电平端测试其电压波形的变化，仿真结果如图7所示。其中红色为C1两端电压变化曲线，中间绿色为C2两端电压变化曲线，蓝色为C3两端电压变化曲线。从图中可以明显看出压缩效果，未压缩时脉冲上升时间约为6.7μs，经过一级磁压缩后脉冲上升时间约为0.67μs，两级压缩后脉冲上升时间为67ns,两级压缩比均为10。C1两端电压约为20.5kV，C2两端电压约为19.8kV，C3两端电压约为18kV，因此第1级压缩效率为93.3%，两级总压缩效率为81.0%。图8为一级和二级压缩后电流脉冲波形图，绿色曲线为C1点脉冲电流变化曲线，蓝色为C2点脉冲电流变化曲线。

Fig.7 Comparison of pulse rise time before and after compression

Fig.8 Current pulse waveform of primary and secondary compression

在上述基础上改变负载电阻大小进行仿真，图9所示为电阻变化时电容各点电压变化的情况。最上方浅蓝色线为C1两端电压变化情况，中间黄色曲线为C2两端电压变化情况，最下方灰色曲线为C3两端电压变化情况。仿真发现在磁开关以纳米晶作为磁芯，总压缩比为100，两级压缩总体积最小的情况下，负载电阻为250Ω时总压缩效率达到最大，为81.9%。在负载电阻小于250Ω时，电路中少量的漏电压很快的消耗在负载电阻上，不能在导通之后与脉冲电压形成累加，导致电阻过小时有一定损耗。随着阻值的增加，漏电压减小，损耗减小。在电阻大于250Ω时，漏电压不再减小，损耗不变导致输出电压不再变化。实际选择负载电阻时考虑体积因素负载电阻不宜过大。

Fig.9 Capacitance voltage changes when resistance changes

图10和图11所示为在不加复位电流和复位电流过小时的各点电压波形图。从图中可以看出，未加复位电流以及一级复位复位电流小于1.09A、二级复位电流小于3.27A时，都会导致在电压未达到设定值时磁开关已经导通，大大降低了压缩效率。同时仿真发现复位电流也不宜过大，在一级复位电流大于9.80A、二级复位电流大于时14.50A时，输出效率在随着复位电流的增加而减小。表3所示为一级复位电流为1.5A时，二级复位电流变化与两级压缩电路效率的关系。其中V1，V2和V3分别表示电容C1，C2和C3两端电压值。图12所示为一级复位电流为15A、二级复位电流为20A时仿真结果图。其中红色为C1两端电压变化曲线，绿色为C2两端电压变化曲线，蓝色为C3两端电压变化曲线。图中可以明显看出一级和二级磁开关饱和时间均增加，且C2两端电压在达到最大值时二级磁开关没有及时导通造成损失。另外由于磁芯中磁畴在无外加磁场时会产生的无规则排列，由磁滞回线可知，在不加复位电路时，磁感应强度值在0值左右是一个不确定的量，导致每次运行时产生的脉冲波形均不相同，影响了电路的稳定性。

Fig.10 Voltage waveform without reset current

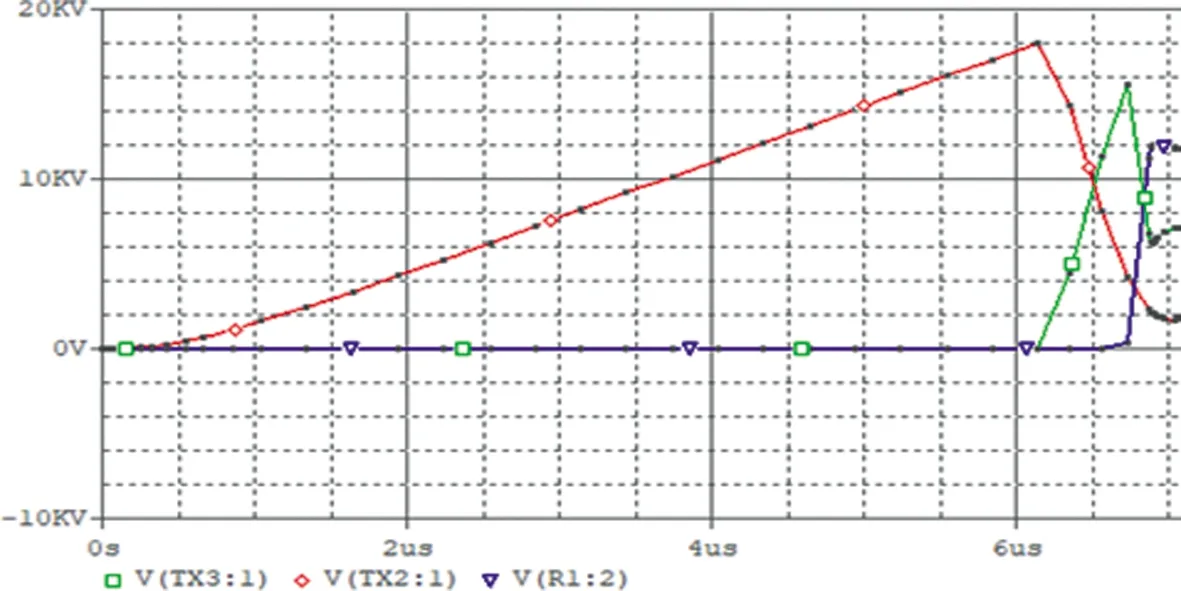
Fig.11 Voltage waveform with small reset current

Table 3 Relationship between total efficiency and secondary reset current

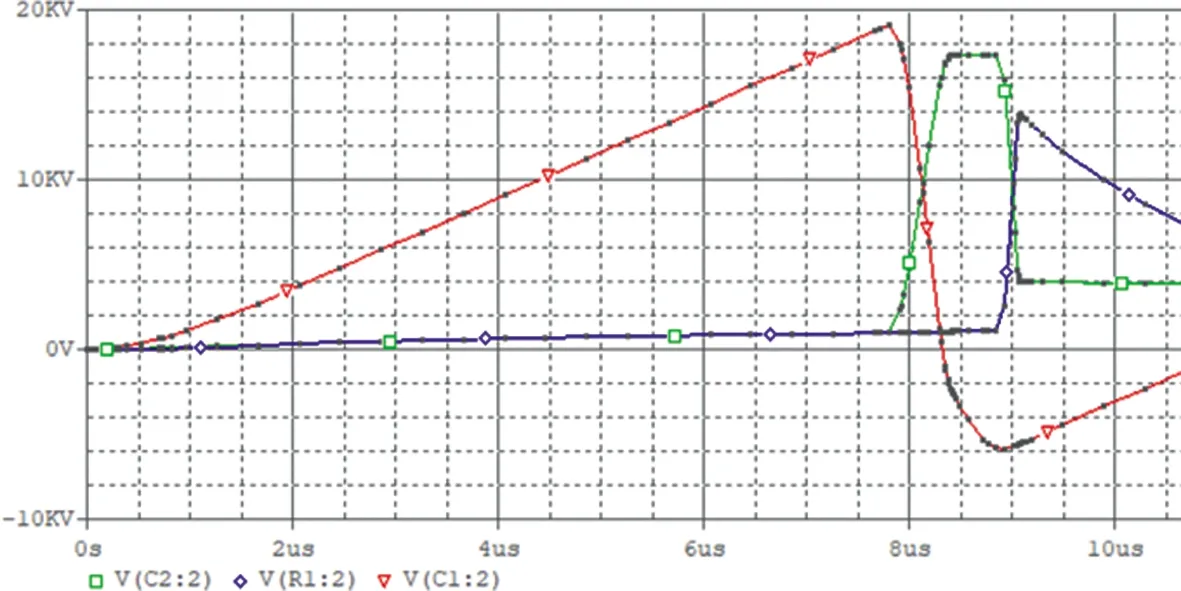
Fig.12 Voltage waveform when the reset current is large

4 结 论

磁芯是磁脉冲压缩电路的核心元件，通过使用PSPICE软件中的Model Editor进行模型的建立和编辑使仿真结果可以更接近实际值。通过相关计算及仿真分析发现，在确定磁芯类型的情况下，不同的压缩比效率不同，磁压缩系统的总体积与各级压缩比相关。在确定磁芯类型以及压缩比的情况下，通过使用PSPICE软件对两级磁脉冲压缩电路的仿真分析发现，在负载电阻较小时系统的效率较低，当大于一定数值时，可取得最大效率。同时分析发现复位电路影响着电路的稳定性及其效率，过小或者过大的复位电流均可以使输出效率降低，因此合适大小的复位电流对磁脉冲压缩电路至关重要。