基于MEEMD-ARIMA 模型的波浪能发电系统输出功率预测

吴 峰，王 飞，顾康慧，周能萍

（1.河海大学能源与电气学院,江苏省南京市211100；2.国网江苏省电力有限公司南京供电分公司,江苏省南京市210019）

0 引言

海洋约占地球总面积的70.8%,蕴藏着巨大的能源。海洋能种类多样,主要有波浪能、潮汐能［1］、盐差能、海风能、温差能［2］等。当前,对潮汐能的开发已大大超过其余海洋能并已进入商业运行阶段,但潮汐电站的建立受地理位置限制较大［3］。相比于其他能源,波浪能发电形式更为灵活,波浪能作为未来化石燃料可行的替代品［4］,能有效缓解因人类生产生活而引发的全球变暖现象［5］。中国的海岸线长达1.8×104km,波浪能储量高达7～17 TW·h［3］,其中,渤海、东海、黄海地区波浪能储量所占比例最大［6］,这在清洁的可再生能源中具有得天独厚的开发潜力［7］。

波浪发电主要依靠波浪的动能通过不同的物理过程产生电能。例如波浪冲击、波浪振荡和波浪越顶等［8］。波浪能虽然有巨大的开发价值,但其随机波动特性的特点给大电网调度和控制带来一定的难度［9］。因此,有效地预测波浪能发电系统的输出功率是进一步开展波浪能电站建设的前提。当前对波浪能发电系统输出功率的研究主要有2 个方向,分别是基于测量波浪能发电系统的实际输出功率来预测未来功率的直接法和基于海浪要素波高和周期进而预测波浪能发电系统输出功率的间接法。由于中国尚未建成波浪能电站,且多数波浪能装置均在试验阶段,缺乏实际运行数据,对波浪能的预测大多采用间接法。一种针对海浪要素预测的方法是采用数值计算,即根据气象部门提供的天气预报作为预测模型的输入,现阶段主要的模型有波浪模型（wave model）、模拟近岸波浪（simulation waves nearshore）模型、稳态波谱（steady-state spectral wave）模型等。上述模型主要作为海洋灾害预报模型,其所需计算的数据量大,有些数据跨度时间长,不适用于电力系统的实时调度。另一种方法根据海浪波面的实时数据建立数学模型,从而对海浪要素进行预测。文献［9］建立了基于风-浪经验模型和灰色模型GM(1,1)的组合预测方法,实现了海浪波高和周期的短期预测,将其代入建立的波浪能发电系统模型得到了系统的预测输出功率。文献［10］建立了自回归滑动平均（ARMA）预测模型,对海面波高进行了超短期预测。文献［11］建立了基于风浪耦合的预测模型,提高了波浪要素的预测精度。

海浪要素难以预测的关键在于海浪波高和周期的随机波动性,这与风电场的输出功率具有相似性。文献［12］基于离散小波变换（DWT）,将风电场输出功率分解为趋势分量和扰动分量,分别采用稀疏贝叶斯理论构建预测模型。但DWT 分解效果取决于小波基函数的选择,对高频分量分辨率较差。经验模态分解（empirical mode decomposition,EMD）方法对数据的分解不需要基函数的选择［13］,线性和非线性序列应用效果较好,能提取序列的局部特征［14］。例如,文献［15］建立了EMD 和人工神经网络（EMD-ANN）的风电场功率的短期预测模型,采用EMD 方法对风电场功率序列进行分解,对高频分量采用神经网络组合预测模型。但EMD 方法分解原始数据时,较易出现模态混淆的现象。文献［16］建立了总体经验模态分解（ensemble empirical mode decomposition,EEMD）和声搜索优化的支持向量机（EEMD-HS-SVM）组合预测模型,EEMD 方法是指在进行EMD 时添加正态分布白噪声,通过EEMD 方法将原始风功率序列分解成一系列本征模态函数（IMF）分量,减少了模态混淆现象。但EEMD 方法计算量大,添加的白噪声不能完全被中和,完备性差［17］。因此,文献［18］提出了改进的EEMD（MEEMD）方法,依据分量排列熵的大小,剔除异常分量,该方法在减少计算量的同时能有效地抑制EMD 方法分解过程中的模态混淆现象。

MEEMD 方法将随机波动特性强的波高数据分解成一系列从高频到低频的分量,差分整合移动平均自回归（ARIMA）模型能根据各个分量的固有趋势分别进行预测。 所以本文提出了基于MEEMD-ARIMA 方法的组合预测模型。基于海浪计算原理,计算混合浪的每小时平均波高与周期。采用MEEMD 方法对混合浪的平均波高与周期进行分解重构,得到一系列特征互异的IMF 分量和余量,分别建立各分量的ARIMA 预测模型。将各分量预测叠加,得到平均波高与周期的预测值。在此基础上建立了直驱式波浪能发电系统的波高-功率转换模型。最后,通过算例对比表明所提方法具有较高的预测精度。

1 海浪理论

1.1 海浪功率谱密度

在海洋中,海浪经常以风浪与涌浪并存的混合浪形式存在［19］。风浪由风直接作用产生并一直处在风的作用下,风浪周期较小、波峰尖削、频率较高。涌浪是当地风停止后或风速突变时,海区内剩余的波浪或其他海区传来的波浪［20］,涌浪周期较大、波峰平缓、频率较小。

由上述内容可知,海浪是由不同频率的风浪与涌浪组成。本文采用数值计算的方法加以区分,文中引入海浪功率谱密度（power spectrum density,PSD）,将时域中海浪的波动特性表示为频域中的能量密度,如式（1）所示。

式中:FFT（·）为快速傅里叶变换；x（l）为海浪的第l 个离散采样序列；N 为海浪样本的个数；Δf=fs/N,fs为样本点采样频率；E（·）为取均值函数。

附录A 图A1 为某次采样的海浪数据计算的功率谱密度,谱中出现明显的2 个峰值,其中分割频率f 为0.157 8 Hz。高频部分为风浪,低频部分为涌浪。关于风涌浪分离的具体细节可参阅文献［19］,此处不再赘述。

1.2 海浪要素计算

直驱式波浪能发电系统输出功率的大小取决于前端一级转换装置所受波浪力的大小,波浪力的大小与波高和周期关系密切。

依据海浪的统计特性,常见的主要有平均波高Ha、有效波高Hs、最大波高Hm。其中,平均波高是采样时间内波高的平均值,有效波高是采样时间内前所有波高数值最大的1/3 的平均值,最大波高是采样时间内最大的波高。本文选取海浪每小时平均波高Ha和平均周期Ta对波浪能发电系统的输出功率进行短期预测,即

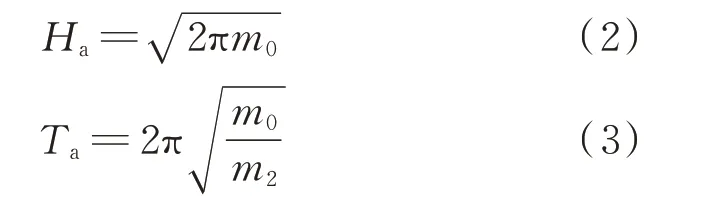
式中:m0为海浪频谱0 阶矩,m2为海浪频谱2 阶矩,m0和m2表达式如式（4）所示。

式中:ω 为海浪的角频率；r 为阶数。

依据上述公式,给出分离后海浪平均波高Ha表达式为:

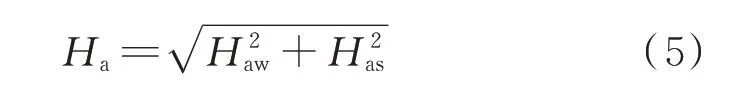
式中:Haw为风浪的平均波高；Has为涌浪的平均波高。

2 MEEMD 和ARIMA 方 法 及 理 论

2.1 MEEMD 方法

MEEMD 方法的实质是在原始信号中成对添加符号相反的白噪声,使原信号极值点的分布更均匀,之后再进行EMD［17］能有效克服EMD 方法存在的模态混淆等问题,MEEMD 方法步骤如下。

步骤1:在初始序列X（t）中,分别添加符号相异的白噪声信号ni（t）和-ni（t）得到新的序列,如式（6）和式（7）所示。

式中:ai为白噪声信号的幅值,i=1,2,…,n,其中,n为添加的白噪声的对数,一般不超过100。

步骤5:对剩余的H（t）进行EMD,最终将所有得到的IMF 分量按从高频到低频排列。

DWT 分解采用基函数db4,MEEMD 和DWT分解结果如图1 和图2 所示。图1 中,IMF1至IMF6表示IMF 分量,RS7表示分解后的余量；图2 中,s1至s5表示DWT 分解分量。可以看出,MEEMD 得到的分量比DWT 分解多,但DWT 分解对高频分量的分解不彻底,对数据的平稳化处理低于MEEMD,分解的分量的波动性强于MEEMD。相比于DWT 分解,MEEMD 的子序列更适用于ARIMA 预测模型。

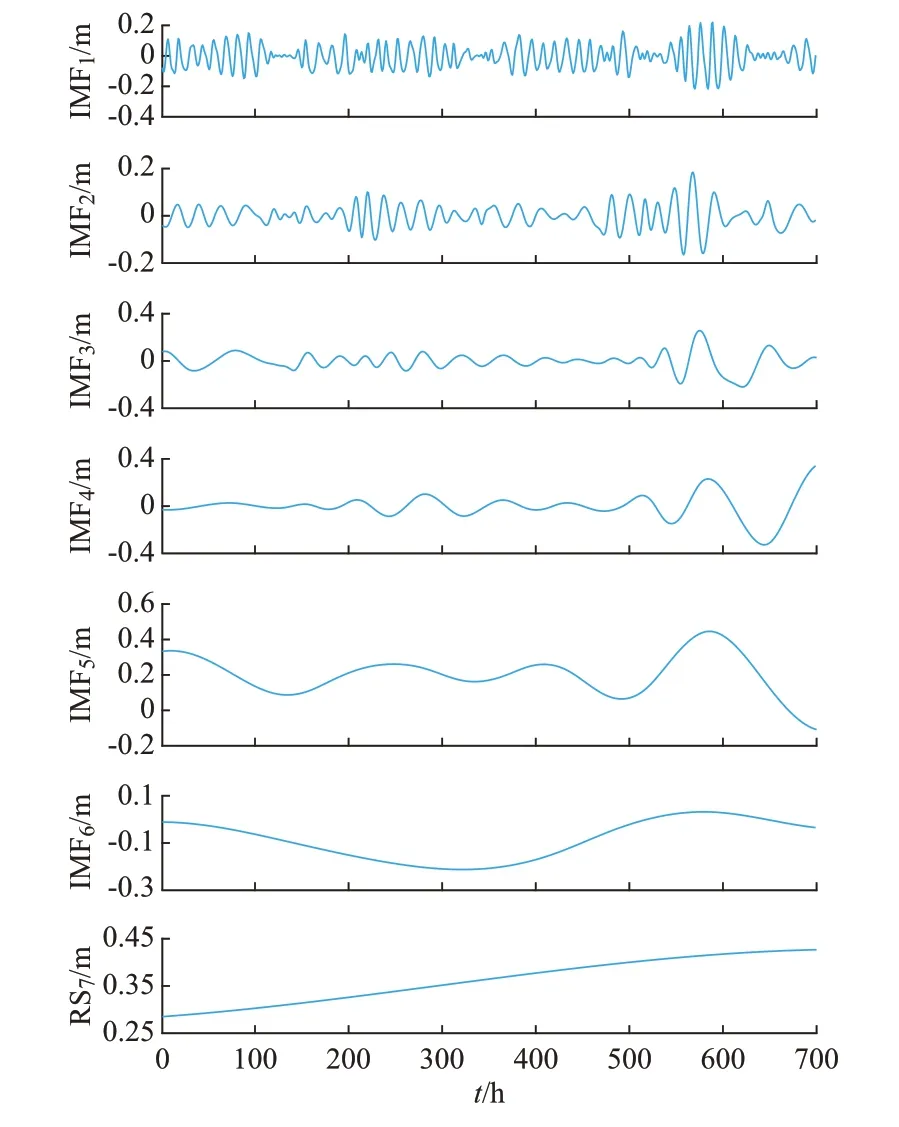
图1 平均波高的MEEMD 结果Fig.1 MEEMD results of average wave height

图2 平均波高的DWT 分解结果Fig.2 DWT decomposition results of average wave height

2.2 ARIMA 预测方法

时间序列分析法广泛应用于电力系统负荷预测、气象预报、经济预测等重要领域。主要有:自回归（AR）模型、滑动平均（MA）模型、ARMA 模型以及ARIMA 模型。时间序列分析法的主要思想是将波动的时间序列平稳化,接着用AR 模型、MA 模型和所选样本的自偏相关函数等数据对平稳化过后的序列进行识别、建模和预测。

由于波浪序列是非平稳的波动序列,本文采用ARIMA 模型,首先将经MEEMD 方法分解后的波动子序列进行差分处理,辨识差分后子序列是否平稳,如不满足平稳要求,则须再次差分,直到满足平稳要求后,用ARMA 模型进行预测。最后,将各子序列的预测结果叠加,得到平均波高与周期的预测值。子序列{ yt}的ARMA 模型具体形式如下［21］。

式中:φ1,φ2,…,φp和θ1,θ2,…,θq为待定系数；p 为AR 模 型 的 阶 数；q 为MA 模 型 的 阶 数；εt为 白 噪 声序列。

3 阿基米德浮子式波浪能发电装置输出功率转换模型

阿基米德浮子式（AWS）波浪能发电装置由二级能量转换装置组成,分别为AWS 与直线式永磁发电机。AWS 装置的结构原理如附录A 图A2 所示,主要由浮子和固定在海床上的空心圆筒组成。当浮子上方经过波浪时,波浪力带动浮子做上下往复运动,从而带动发电机动子切割磁感线产生电能。

AWS 波浪能发电系统的简化机械模型如式（10）所示。

式中:mtot为系统所有运动部件的质量总和；βg为直线式永磁发电机的阻尼系数；βw为AWS 装置的水动力阻尼系数；ks为AWS 装置的弹性系数；x 和v 分别为浮子的位移和直线式永磁发电机动子的速度；Fwave为发电系统浮子所受的波浪力。

文献［22］表明,只有当AWS 装置与波浪产生共振时,才能最大限度地捕获波浪能量,此时βg=βw,本文采用其提出的周期T 内所捕获的总波浪能Ew的计算公式,即

式中:pw为波浪能发电装置的实时功率；Fmax为周期内最大波浪力。

文献［23］详细分析了波浪力的模型,计算公式如下。

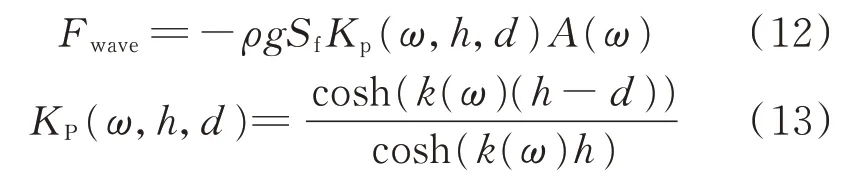
式中:ρ 为海水密度；g 为重力加速度；Sf为浮子的受力面积；h 为海水深度；d 为浮子到海面的距离；A（ω）为波面数据；KP（⋅）为水深d 的压力系数；k（ω）为波数,k（ω）=ω2/g。

将式（12）代入式（11）中,可得到波浪能发电装置的平均功率为:

式中:η 为波浪能装置的转换效率,本文取值为0.5。

4 实例分析

本文的波浪数据来源于中国江苏大丰外海的波浪观测站,收集数据的OSB-M3Ⅱ水文气象浮标系统位于外海10 m 深处。该系统对波浪的采样频率为2 Hz 或4 Hz,每小时进行一次数据采集,每次记录1 024 s。全部数据包含了2013 年3 月至12 月的实时波浪数据及风速。本文选取2013 年9 月每小时平均波高与周期数据进行建模预测。具体的波浪数据如附录A 图A3 所示。

首先用MEEMD 方法对混合浪波高进行分解,得到6 个IMF 分量和1 个分解下来的余量,分解结果如图1 所示。再对IMF 分量和余量依据最优拟合准则如贝叶斯信息准则（BIC）,选择合适的p 和q 值进行建模预测后,将预测的结果叠加得到最终的预测值。本文采取多步预测的方式,利用2013 年9 月前28 天共672 个数据来预测第29 天的波高。当预测的步长选取为6 时,预测的结果较好,也符合电网短期负荷调度的要求。混合浪每小时平均波高预测结果如图3 所示,不同预测模型的预测误差如表1 所示。表中,MAPE 表示平均绝对百分误差,RMSE表示均方根误差。

图3 2013 年9 月29 日预测与实际波高值对比曲线Fig.3 Comparison curves of predictive and actual values of wave height on September 29，2013

表1 预测误差分析Table 1 Analysis of prediction errors

从图3 和表1 中可以看出,直接采用ARIMA 模型对每小时平均波高数据进行预测的误差较大。随着对平均波高数据解耦,进行风涌浪分离、DWT 分解与MEEMD,数据的波动性进一步降低,预测的精度逐步提高。MEEMD-ARIMA 模型的预测数据走势与实际值相近,预测值与实际值相匹配,预测误差在可接受范围之内。MEEMD-ARIMA 模型相比于其他3 种模型在精度上有了较大的提高,这是因为MEEMD 将波动剧烈的波高序列解耦成较为平稳的子序列,减少了由于序列波动剧烈对ARIMA模型的影响,分解的子序列更适用于ARIMA 模型。MEEMD-ARIMA 模型能基本预测出一天中波高的变化情况,能满足实际电力调度的需求。

对混合浪每小时平均周期采用的预测方法与每小时平均波高相同,其中MEEMD-ARIMA 模型的预测效果优于DWT-ARIMA 和ARIMA 模型,RMSE 为0.184 7 s,MAPE 为3.91%,具体模型对比结果见附录A 图A4 和表A1。

将计算结果代入波高-功率转换公式,即可得到AWS 波浪能系统的输出功率预测值。

功率的预测值与实际值相近,与一天中功率的变化基本相符合,如图4 所示,其中RMSE 为39.54 W,MAPE 为11.59%。浪能装置功率的变化与一天中波高的变化情况相近,说明了波高较大程度地影响了波浪能装置的输出功率。

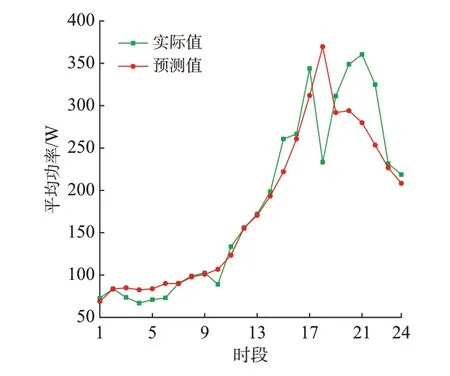
图4 波浪能发电系统输出功率预测曲线Fig.4 Prediction curves of output power for wave energy generation system

5 结语

本文采用间接预测的方法,对波浪要素进行预测。提出了基于MEEMD-ARIMA 方法的波浪能系统短期功率预测模型,预测出平均波高及周期,并将预测数据代入AWS 波浪能发电系统功率转换模型,得到最终功率预测值,并通过实际算例表明该模型预测精度的有效性。

需要指出的是,由于中国尚未建成波浪能电站,波浪数据的选取来源于有限的资料,波浪功率预测的准确性有待于今后实践的检验。随着国家对海洋能的大力开发,数据的积累会不断增加,选取的数据更符合实际波浪情况,波浪功率的预测精度会提高,甚至可以直接对波浪能装置输出功率进行预测。同时本文中的功率预测针对的是单一波浪能装置,可以考虑对尾流效应和时滞效应影响下的大规模AWS 波浪能发电场的输出功率预测。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。