基于组轨迹模型及其研究进展*

张晨旭 谢 峰 林 振 贺 佳 金志超△

【提 要】 在医学研究中存在许多随时间推移动态变化的变量。传统数据处理方法通常取变量在某时点的值或某段时间的均值进行研究和比较，但是这种做法存在一些不足，如数据信息利用不充分、结果难以反映动态过程。基于组轨迹模型是近年来提出的研究变量随时间变化的发展轨迹的一种方法，它在处理纵向数据中具有一些独特优势。本文阐述了基于组轨迹模型的基本原理及其具体形式，并介绍了模型的最新进展及其在应用中的一些误区，在此基础上对模型的研究趋势进行探讨。

在医学研究领域，有许多随时间变化的变量，它们遵循不同变化过程。发展轨迹(developmental trajectory)可描述变量随时间的变化，动态反映变量特征。传统分析发展轨迹的典型方法有分层建模(hierarchical modeling)及潜在曲线分析(latent curve analysis)，它们通过连续分布函数对发展轨迹进行建模，得到变量的总体平均轨迹并揭示预测因素与个体关于平均轨迹的变化之间的联系，但它们对总体内包含不同发展轨迹的情形难以处理，而基于组轨迹模型(group-based trajectory model，GBTM)能够识别总体中不同的发展轨迹，研究轨迹与预测因素或结果间的联系。

基于组轨迹模型最早出现于犯罪学领域。Nagin[1]等应用非参混合泊松模型对犯罪生涯进行建模。他们随后对模型进行了改进，包括扩展可用数据类型、将变量与组成员概率关联及提出确定最优组数量的方法，得到半参基于组的模型[2]。模型假定总体内存在一些遵循相似发展轨迹的成员集群，即“组”，用不同“组”的分布集合近似总体分布，进而用“组”间差异来反映成员特征的差异。

轨迹模型在处理纵向数据方面有独特优势。首先，它能充分利用时依变量信息；其次，模型使用正式统计结构，能够区分随机变异和真实差异；同时，模型可以以图形化的方式呈现，既易于理解又方便不同领域间的交流[3]。

近年来，轨迹模型在医学领域的应用不断丰富，包括探索总体中可能存在的亚组[4]、按基线指标分层研究分组与结果间的联系[5]、揭示分组与基线协变量及预后结果之间的关联[6]、研究协变量与分组对结果影响的交互作用[7]、应用基于组多轨迹建模(group-based multitrajectory modelling)根据多种指标识别分组[8]、依据病人分组进行预测研究[9]等。

基于组轨迹模型

1.基本模型

基于组轨迹模型有两个基本成分：(1)每组的预测轨迹；(2)总体中随机选择的成员属于每个组的概率。

用Yi={yi1，yi2，…，yiT}表示成员i在T时间内指标的纵向测量值。假定总体中存在j个相互离散的组。以P(Yi)表示Yi的概率，有：

(1)

式中πj表示总体中随机选择的成员属于组j的概率，Pj(Yi)表示成员在组j时得到Yi的概率，即Yi的概率分布函数。

基于组轨迹模型假定变量值在时间线上具有条件独立性(conditional independence)，即轨迹组j中的成员在t时间的变量值yit独立于其在之前时间的值yit-1，yit-2，…，因此：

(2)

式中pj(yit)为给定成员在组j时yit的概率分布函数。进行条件独立假定可简化建模过程。

模型的参数通常由极大似然估计法(maximum likelihood estimate，MLE)估计得到。实际应用时，式(1)中Pj(Yi)的具体形式一般由数据类型决定。

(1)似然函数的具体形式

在建模之前，需要对数据的分布形式加以指定，模型处理不同类型数据时需要两个关键成分：(1)描述数据分布特性的函数；(2)变量值与年龄(或时间)的函数，即链接函数(link function)。

(3)

(4)

Smin和Smax分别为数据的最小值与最大值。由正态分布累积密度函数可得：

(5)

当数据服从泊松分布时，链接函数为：

(6)

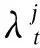
相应的概率分布函数为：

(7)

式中pj(yit)表示yit取任意非负整数值的概率。每种可能结果的概率取决于t时间所有成员的事件平均发生率λjt。

对于遵循二分类逻辑分布(logit distribution)的数据，同样借用潜变量处理：

(8)

(9)

除上述三种数据类型外，其他数据也可用基于组方法来处理，Elmer[10]等探讨了将基于组轨迹模型应用于不服从正态分布但符合β分布的定量数据。结果表明，数据得到良好的拟合。这类研究拓展了基于组轨迹模型的应用范围。

(2)组成员概率

式(1)中组成员概率πj表示总体中属于组j的成员比例，即随机选择的成员遵循组j轨迹的概率，通常以如下形式指定：

(10)

其中θj，j=1，2，3，…，J为要估计的参数，这种形式可以保证πj取值在0和1之间且所有πj总和为1。

2.组数量及多项式阶数选择

基于组轨迹模型目的是识别遵循不同轨迹的组。在建模之前，通常需要选择模型组数及链接函数的多项式阶数。常用的选择过程分为两步，首先为所有组指定固定的多项式阶数，依据标准判断最优组数，然后固定组数选择最优多项式阶数。

判断组数的标准有客观标准和主观标准。用于判断混合模型中最优成分数量的客观标准很多。包括假设检验、信息标准、分类标准、最低信息比率标准[11]。目前轨迹模型尚无公认最优客观标准，但已发表文献中贝叶斯信息准则(Bayesian information criterion，BIC)应用较多：

BIC=log(L)-0.5klog(N)

(11)

BIC平衡了组数增加时模型复杂性的增加及拟合性能的改善。通常选择BIC值最大的组数及多项式阶数，对不同BIC值的备选模型进行判断时，可根据量表选择最优模型[12]。

通常情况下客观标准可作为建模依据，但主观判断亦必不可少。当BIC值随组数增加单调递增时用客观标准难以作出判断，可结合专业知识指定组数或多项式阶数。最终模型应在充分呈现数据特征的同时兼具简洁性[3]。

许多学者针对模型组数选择及数据分布假定作了深入研究。Klijn[13]等基于R软件开发了一种图形化的工具——拟合标准分析图(fit-criteria assessment plot，F-CAP)。它可简化备选模型的分类列举过程并图形化地呈现不同组数下各指标值的变化，从而辅助选择最优组数。Elsensohn[14]等提出了用包络图(envelope plot)来评估模型分布假定的方法。他们对四种不同分布情形进行了模拟分析，结果表明通过检查包络图中变异区间宽度及上下限线条平行程度可以直观地验证残差的方差齐性假定。Shah[15]等提出了两种模型判别指标：判别指数(discrimination index)和修正熵(modified entropy)。它们可以快速有效地识别模型结果中可能不属于某组的成员。

轨迹模型通常作出条件独立性、组间方差齐性及方差的时间稳定性假定。Davies[16]等探索了违背上述假定情形下模型的性能。他们对潜在分类增长分析(latent class growth analysis，LCGA)、增长混合建模(growth mixture modelling，GMM)和多元高斯混合建模(multivariate Gaussian mixture modelling，MGMM)3种建模方法下的18种情形进行了模拟研究，结果表明在违背假定的情形下应用基于传统假定的方法如LCGA及MGMM进行建模会产生较大的误分类，这时应用GMM进行建模可能更好。

3.组成员后验概率

组成员后验概率(posterior probabilities of group membership)表示具有某些特征的成员属于轨迹组j的概率。后验概率有重要意义，它不仅为组分配提供了客观依据，也可以用来创建轨迹组成员描述(profile)及评估模型的数据拟合质量，还可作为权重计算轨迹组成员结果期望值或探索协变量与分组间的联系。

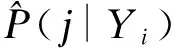
(12)

4.模型的扩展

(1)包含协变量

变量特征不同的成员可能遵循不同的发展轨迹。模型通常可纳入两种协变量：普通协变量和时依协变量。普通协变量是模型建立前就存在且固定不变的变量，时依协变量值可随时间而变。二者在模型构建过程中有所区别。

在模型中纳入协变量常用三步法[3]。首先，在基础模型中确定最优组数和多项式阶数。其次，识别协变量对分组的影响是否显著，可以通过基于z分数的检验及Wald检验判断协变量系数是否有意义及组间差异是否有意义。最后，联合估计参数，得到最终模型。

除三步法外，也有学者进行了其他方法的探索。Block[17]等提出了“一步法(one-step approach)”，这种方法解决了三步法可能低估协变量与组成员间关联的问题。Davies[18]等使用Mplus模拟比较了6种纳入协变量的方法，结果表明所有方法中一步法偏倚最小，但由于计算的复杂性会随协变量增加而加大，一步法有时难以实现，其他方法中，I3S方法的表现较好。在应用中可根据研究目的和数据特点进行方法选择。

(2)双轨迹模型和多轨迹模型

在医学研究中，经常会遇到需要探索纵向数据变量之间关系的情形，双轨迹模型(dual trajectory model)和多轨迹模型(multi-trajectory model)可处理此类问题。

双轨迹模型可以研究两变量间的关联。它通常为每个单独的变量建立轨迹模型，然后通过两变量不同组的两两关联概率将两模型相联系。与基础模型相比，它能够探索两变量关联的具体形式。

当研究两个以上变量间关系时，可应用多轨迹模型，它与双轨迹模型在形式上有所区别。双轨迹模型在变量组数较多时关联概率数量庞杂且难以解释，而多轨迹模型可以构建包含所有变量的模型，模型每个轨迹组都由多条轨迹构成，每条轨迹对应一种变量。这种建模形式可以简化模型并提高可解释性[19]。

Nagin[20]等构建了多轨迹模型的似然函数并用实例呈现了建模过程。首先为每个指标变量分别建立轨迹模型，观察每个模型的组数及特点，然后按照能够呈现变量数据特征及使拟合指标达到最优的原则，在模型充分性指标的约束下，确定最终模型。

5.模型实现

目前主流的统计软件SAS、R及stata均可实现基于组轨迹模型。其中SAS中Traj过程步的应用比较常见[12]，Stat常用Traj包进行建模[21]，R中也可通过扩展包实现(表1)。

表1 三种统计软件对基于组轨迹模型的实现

模型应用误区

基于组轨迹模型在处理纵向数据时有许多优势，但在应用中也存在一些误区。

首先，对模型中“组”的理解。“组”是一种统计虚构，而非客观事实，模型分组信息要和具体事实相区分。例如临床研究中针对某项指标建立模型并给予病人分组并不意味着病人一定属于疾病某个亚型。轨迹模型是数据驱动的，它更倾向于呈现数据特征，且模型中组的数量并非固定不变[22]。

其次，根据后验概率分组存在不确定性。在建模过程中，每个成员都依最大后验概率分配到某个组。虽然模型诊断指标有组均后验概率不小于0.7的限制，但同一组中以不同概率分配到该组的成员间分组确定性不同。忽视不确定性直接进行分析会带来诸多问题[3]。将分组作为变量进行分析时，应对这种不确定性加以考虑。

小结与展望

基于组轨迹模型由于其对纵向数据处理的优势，目前正在医学领域得到越来越广泛的应用，相比传统数据处理方法，它可以从纵向数据中识别出不同的发展轨迹进而为临床诊疗提供参考，因此对模型理论体系及其应用进行深入探索非常有意义。本文阐述了基于组轨迹模型基本理论及其最新进展，并在此基础上讨论了模型应用中容易陷入的误区。

目前，基于组轨迹模型在应用中仍然存在诸多问题。首先，组数选择尚缺乏统一的最优判断标准。其次，现有关于模型结果报告的可用指南较少[23]，对模型在医学领域中应用的指导有待完善[24]。同时，模型对缺失数据的处理方法不够成熟，已发表文献探索了模型在非随机缺失机制下的实现[25]，但在其他类型缺失机制方面仍待探索。此外，模型扩展形式，如多轨迹模型，在选择组数时操作复杂且缺少客观标准，尚需深入研究。