依时ROC分析方法学综述*
2021-01-09中国医学科学院基础医学研究所北京协和医学院基础学院统计学教研室100005王子兴申郁冰姜晶梅
中国医学科学院基础医学研究所/北京协和医学院基础学院统计学教研室(100005) 王子兴 申郁冰 姜晶梅
医学中常常需要评价某种标志物、影像指标或评分工具对疾病发生、诊断和预后的预测性能[1]。受试者工作特征(receiver operating characteristics,ROC)曲线分析是面向上述研究目标的一类统计学方法,其基于“金标准”将疾病状态进行二分类,进而综合分析待评价指标各阈值所对应的灵敏度、特异度信息。然而疾病状态与时间有关,可经历“从无到有”的变化过程[2]。这种依时间而改变的结局变量给预测性能的评价带来两方面问题:①基于不同时间截面的分析会有不同的疾病状态分布;②疾病状态可发生删失,且删失比例随研究时间的延长而增高[3-4]。为实现对该类含删失的时间-状态数据的预测性能评价,经典ROC曲线和生存分析方法进行结合产生了依时ROC(time-dependent ROC)分析方法[5]。依时ROC在过去20年内得到了极为迅速的丰富和发展,并应用于疾病预防、药物治疗等领域。
本文从非参、半参角度总结依时ROC分析的方法学研究及其对应的软件实现方式,以便增进读者对依时ROC方法的了解并在临床转化中的应用提供参考。
基本定义
1.病例和对照的三种定义
依时ROC除标志物X阈值c外,还需结合时间阈值t进行分析(图1),由此产生三种依时ROC的“病例”和“对照”定义,这些定义最早由Heagerty和Zheng于2005年总结[6]并得以沿用。

图1 依时ROC三种定义示意图
累积/动态(cumulative/dynamic,CD)定义下,累积病例为研究起始点到t时刻期间经历事件的个体(图1中的A、B和E),动态对照为t时刻仍未发生事件的个体(图1中C和F)。可见CD定义下病例和对照集均随着时间变化而改变,某个体可能在前后分别作为对照和病例,故存在信息被重复利用的问题[7]。然而CD定义具备鲜明的临床意义,可用于预测个体是否在指定时间内发生感兴趣结局,故得到了最大程度的方法学发展和应用[2]。
时点/动态(incident/dynamic,ID)定义下,时点病例为指定时点t上恰好发生事件的个体(图1中的A),而动态对照同前。ID定义可利用其与生存分析中风险集概念的对应关系得到一些简化估计方法。
时点/静态(incident/static,IS)定义下,时点病例同前,而静态对照为在某固定随访期(O,t*)内未发生事件的个体(图1中的C),其中t*需足够长来观察终点事件。IS定义主要面向筛查研究。
2.符号定义
以n表示观测总数,Xi(i=1,…,n)表示第i个观测的标志物取值(不失一般性,假设标志物值越高事件发生时间越短)。Ti(i=1,…,n)表示第i个观测的结局事件理论发生时间。Zi=min(Ti,Ci)为观察时间,其中Ci为删失时间。δi=1(Ti≤Ci)为删失指标,其中1(·)为示性函数。
分析方法
1.问题转化
灵敏度Se(c,t)和特异度Sp(c,t)是依时ROC的决定因素。以CD定义为例,定义个体标志物X取值大于阈值c为阳性,则依时ROC下的灵敏度和特异度可分别表示为
Se(c,t)=P(X>c|T≤t)
(1)
Sp(c,t)=P(X≤c|T>t)
(2)
上式利用了贝叶斯定理进行变换,目的在于将问题转化为给定X取值下的事件发生时间分布,以便更容易依据生存分析方法进行估计(尤其是对删失的处理)。可见对依时ROC指标计算的关键在于估计X和T的联合分布[8],下文从非参、半参方法两个角度进行总结。
2.非参方法
(1)Kaplan-Meier法
由Heagerty等人于2000年[5]提出。将式(1)和(2)改写为生存函数形式
(3)
(4)
其中,S(t)为生存函数,S(t|X>c)是X>c时的条件生存函数,FX(c)是标志物X的经验分布函数,FX(c)=∑1(Xi≤c)/n。
对生存函数S(t)采用Kaplan-Meier法估计
(5)
Tn为观察时间Zi值的集合。
Kaplan-Meier法简单易理解,但其获得的灵敏度和特异度不具有单调性且不能确保落在[0,1]区间,违背上述指标的基本特征。另外,生存函数的估计建立在删失独立于标志物的条件下,该条件不满足时会使得对结果的估计不稳定。
(2)最近邻估计法
考虑Kaplan-Meier法的上述问题,Heagerty等人[5]同时提出了基于二元生存函数的最近邻估计法(nearest neighborhood estimation,NNE)。假定删失基于标志物X条件独立,从而采用S(t|X)而不是S(t)进行灵敏度和特异度的估计。以NNE估计(X,T)的二元分布,条件生存函数的计算式为
(6)

于是,灵敏度和特异度为
Se(c,t)=P(X>c|T≤t)
(7)
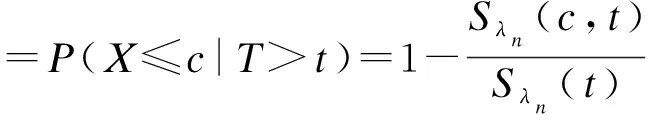
(8)

(3)风险集递归算法
Chambless等人[9]于2006年基于生存分析中风险集的概念提出了一种类似于Kaplan-Meier法的递归算法。首先对观察时间从小到大排序,令tk为排序后第k个观测的观察时间,tm为时刻t前的最后一次观察到的事件的观察时间。Blanche[10]等人在此基础上给出了灵敏度和特异度更加直观的表达。
(9)
(10)
其中,d(k)是在tk时发生事件个体的指标,I(Xd(k)>c)=P(Xi>c|tk-1 与最近邻估计法相比,风险集递归算法不涉及任何平滑参数直接得到生存函数,亦可保证灵敏度单调且范围为[0,1],但其特异度不单调且应用于大型数据集时计算量大,故应用并不广泛。 (4)非条件/条件逆概率删失加权法 逆概率加权的思想最早由Uno等人[11]于2007年引入依时ROC分析,经Hung等人[12]于2010年发展,以非删失概率的倒数(即逆概率)作为权重,故称非条件逆概率删失加权法(inverse probability censoring weighting,IPCW)。进一步,Blanche等人[10]于2013年改用条件删失逆概率作为权重,称为条件IPCW。非条件IPCW的灵敏度为 (11) 其中,SC(Zi)是在观察时间Zi上的删失生存函数(即非删失概率)。特异度为 (12) 将式(11)中的SC(Zi)更换为SC(Zi|Xi),可得到条件IPCW的灵敏度估计 (13) 而此时的特异度也需做条件生存函数的转化,为: (14) 其中,SC(t|Xi)=P(Ci>t|Xi)。 删失生存函数和条件生存函数均可采用KM估计,后者的优势在于其兼容不独立于标志物的删失,即删失与标志物取值有关的情形。 (5)个体信息条件加权法 Li等人[13]于2016年提出一种容易理解且高效的加权算法。将研究对象在时刻t的状态划分为四组:对照(Zi>t)、病例(Zi≤t且δi=1)、此刻删失(Zi=t且δi=0)、已经删失(Zi Wi=P(Ti≤t|Zi,δi,Xi) 其中,S(t|X)=P(T>t|X)为条件生存函数,可用核加权KM估计。 灵敏度、特异度分别为: (15) (16) 该方法的优势在于:灵敏度和特异度关于阈值c单调;自动解释了删失时间C与标志物X之间可能存在的相关性;核加权KM估计对带宽的选择不敏感。 (6)加权平均秩法 基于ID定义和风险集个体得分的排序思想,Saha-Chaudhuri等人[14]于2013年提出加权平均秩法。该法的特点为不需计算灵敏度和特异度,而直接基于给定t时刻的局部一致估计得到依时ROC曲线下面积(area under curve,AUC): (17) (18) 其中,Nt(hn)=(tj:|t-tj| (19) 其中,Khn是标准化的核函数,满足∑jKhn(t-tj)=1。式(19)是式(18)的平滑形式。该方法的假设为删失时间C独立于事件发生时间T。 (7)二元核密度估计法 CD定义下的灵敏度和特异度: (20) (21) ID定义下的特异度与式(21)相同,而灵敏度: (22) 3.半参方法 非参方法对函数形式假设条件较少,使用灵活,但逐点拟合过程计算量大。半参数法通过一定假设条件减少计算量,同时避免了参数法严格的条件限制[1]。 (1)非等比例Cox模型 ID定义与Cox比例风险模型中的风险函数直接对应。由此Heagerty等人[6]2005年提出将比例风险回归参数γ引入Cox模型,为了放宽Cox模型中等比例的假设条件,将固定比例γ扩展为依时协变量系数γ(t)。 则灵敏度为: (23) 特异度为: (24) (2)Cox平均生存概率法 一般而言阈值取值较大时对应的样本量较少,影响对条件生存函数S(t|Xi)估计稳定性。Chambless等人[9]2006年针对该问题提出了基于Cox模型“得分”的估计方法。其通过Cox比例风险模型估计风险因素的系数,进而估计生存函数。其灵敏度和特异度分别为: (25) (26) 其中M=XTβ是生存函数的得分。该方法产生单调的敏感度和特异度,且删失可以不独立于标志物取值。 (3)条件绝对风险函数法 Viallon等人[15]于2011年阐述了预测曲线与AUC的对应关系,进而提出一种基于条件绝对风险函数(conditional absolute risk function)直接估计依时AUC的方法,其通式为: (27) 其中,F(t;Xi)=P(T≤t|X=Xi)为条件绝对风险函数,Xi表示排序后第i个观测标志物的值,可采用Cox比例风险模型、Aalen可加模型等方法进行估计。 (4)分数多项式估计法 基于ID定义,Shen等人[1]2015年提出一种采用分数多项式直接估计AUC(t)的方法。令η(·)为连接函数,如logit函数,利用K阶分数多项式进行建模 (28) (5)贝叶斯半参估计法 Zhao等人[16]2016年采用线性相关的狄利克雷过程(the linear-dependent Dirichlet process,LDDP),基于MCMC抽样估计标志物的分布函数和给定标志物取值下的事件发生时间的条件分布。假设事件发生时间已经转换为对数形式。 CD和ID定义下灵敏度分别为: (29) (30) 其中,f(t|Xi)为条件密度函数,F(t|Xi)为条件累计分布函数,可通过LDDP混合模型计算得到。 CD、ID定义下的特异度均为: (31) 其中,S(t|Xi)=1-F(t|Xi)为条件生存函数。 依时ROC分析可通过多种软件实现。以R语言为例,依时ROC相关package见表1,读者可在https://cran.r-project.org检索并查阅相应帮助文档。此外,DIVAT网站(http://www.divat.fr/en/softwares)也提供了一系列用于特殊目的的依时ROC分析R package,如用于生物微阵列数据预后标志物分析的ROC632。 表1 依时ROC分析方法R语言软件包 近年来,依时ROC分析方法不断与医学研究数据和应用需求结合,其方法学研究领域随之不断拓宽,包括但不限于以下发展趋势: 1.重复测量数据纵向标志物的依时ROC分析[17-19]; 2.考虑竞争风险的生存分析评价[10,20-23]; 3.除常见的右删失外,左删失和区间删失的依时ROC分析[23-24]; 4.标志物存在缺失时性能的评价[25-26]; 5.特殊设计类型,如病例队列研究、巢式病例对照研究下依时ROC分析[27-28]; 6.多标志物的综合评价[29-30]。 由于扩展了经典ROC曲线的时间维度,依时ROC在临床应用方面蕴藏着巨大的价值[7]。阳性预测值等指标的估计方法[31],及以最大化患者效用值为目标的精准分层方法[32]探讨,一定程度上促进了依时ROC方法向临床应用的转化过程。然而,依时ROC分析方法的快速发展在一定程度上超过了医学研究者的应用速度,国内研究中的应用尚且较少[3,33-34]。如何针对所研究的问题在众多依时ROC分析方法中进行选择,仍需要开展比较统计学研究。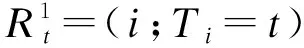

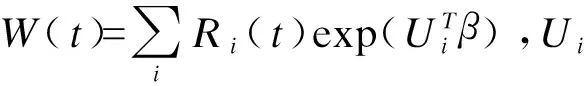

软件实现

趋势和展望
