决策树模型与logistic回归模型在生活饮用水水质影响因素分析中的应用*

渭南市疾病预防控制中心(714000) 焦莉萍 郭晶晶 杨云云 魏明敏 刘 玮 张系忠 沈 托 苗美荣

【提 要】 目的 使用决策树中的分类方法CHAID模型和logistic回归模型分析影响生活饮用水水质的相关因素，并比较两种模型分析结果的异同。方法 采用分层随机抽样的方法对渭南市2015-2017年452座集中式供水水厂的相关因素进行分析，并用受试者工作曲线(ROC)评价两种预测模型的效果。结果 logistic回归分析结果显示，消毒方式、正式运营时间、总投资和供水覆盖人口是水质不合格的影响因素，工程不消毒、工程运营时间越长，水厂规模(总投资和供水覆盖人口)越小，水质不合格率越高。决策树CHAID模型分析结果显示，消毒方式、总投资、供水覆盖人口、正式运营时间、监测点类型是水质不合格的影响因素，工程不消毒是水质不合格的主要影响因素。决策树模型ROC曲线下面积稍大于logistic回归模型(0.725 vs 0.701，Z=3.623，P<0.001)。结论 CHAID决策树模型在水质影响因素风险评估方面有一定的应用价值，与logistic回归模型结合应用可从不同方面对水质影响因素进行分析预测，为后期饮用水的监管工作提供一定的科学依据。

决策树法(decision tree)可以弥补传统统计学分析方法的缺陷和不足[1]。决策树方法能自动检测并估算出众多自变量之间的交互效应，且不受多重共线性的影响，还可以更好地处理极值和缺失值[2]。本文用logistic回归分析法和决策树CHAID法对水质结果的影响因素进行分析，对渭南市水质监测结果现况调查数据建立决策树模型与logistic回归模型，并对两者分析结果进行比较。

对象与方法

1.研究对象

采用分层随机抽样的方法，选取2015-2017年渭南市临渭、澄城、合阳、大荔、蒲城、富平、白水、华阴、华洲、潼关10个县(市、区)108个乡镇的452座农村集中式供水水厂进行分析，这些水厂均为监测点，分别在丰水期和枯水期取1份出厂水和1～2份末梢水进行监测，共2539份水。检测项目包括感官指标、一般化学指标、毒理学指标和微生物指标。

2.研究方法

依据GB 5749-2006生活饮用水卫生标准，对生活饮用水常规项目及氨氮进行检测并判定结果，水质监测结果设置为因变量，合格赋值0，不合格为1。本文收集了影响水厂水质的因素：水源类型、水期类型、消毒方式、监测点类型、正式运营时间、总投资、日供水能力、供水覆盖人口数、卫生许可、水样类型，将这些因素设为自变量，根据自变量与因变量的特征，选择决策树CHAID法与logistic回归分析法对影响因变量的因素进行分析。

3.统计分析原理

根据饮用水检测结果及其相关因素分别建立决策树CHAID模型和logistic回归模型，比较分析结果的异同。CHAID即chi-squared automatic interaction detector，卡方自动交互探测[3]。CHAID法会产生多个树节点，在每一个节点会有不同数目的分支来分割数据，用来建立决策树；其分类的原理则利用卡方检验进行检测分支，根据得到的P值来决定是否仍继续进行分支。logistic回归属于传统型统计学分析方法，属于概率型非线性回归[4]，它研究自变量和因变量之间的依存关系，通过回归分析进行变量的分类与预测。

4.统计分析

本文以水质监测结果为因变量(合格为0，不合格为1)，对自变量进行量化赋值，采用SPSS 17.0统计软件对资料进行CHAID算法分析和logistic逐步回归分析，检验水准α=0.05。根据分析结果找出影响生活饮用水水质的重要因素。利用Medcalc 15.8软件对两种预测模型生成的预测值进行比较，以水质分析结果为状态变量绘制logistic回归模型和CHAID模型生成的受试者工作特征曲线(receiver operating characteristic curve，ROC)，以此曲线判断模型优劣，P<0.05为差异有统计学意义。

结 果

1.基本情况

2015-2017年共选取452座农村集中式供水水厂，根据相关因素对自变量进行赋值，水质监测结果设置为因变量。将水源类型、水期类型、消毒方式、监测点类型、正式运营时间、总投资、日供水能力、供水覆盖人口数、卫生许可、水样类型设置为自变量，并对变量进行相应的赋值，见表1。

表1 饮用水水质影响因素赋值表

表2 饮用水水质影响因素单因素分析结果

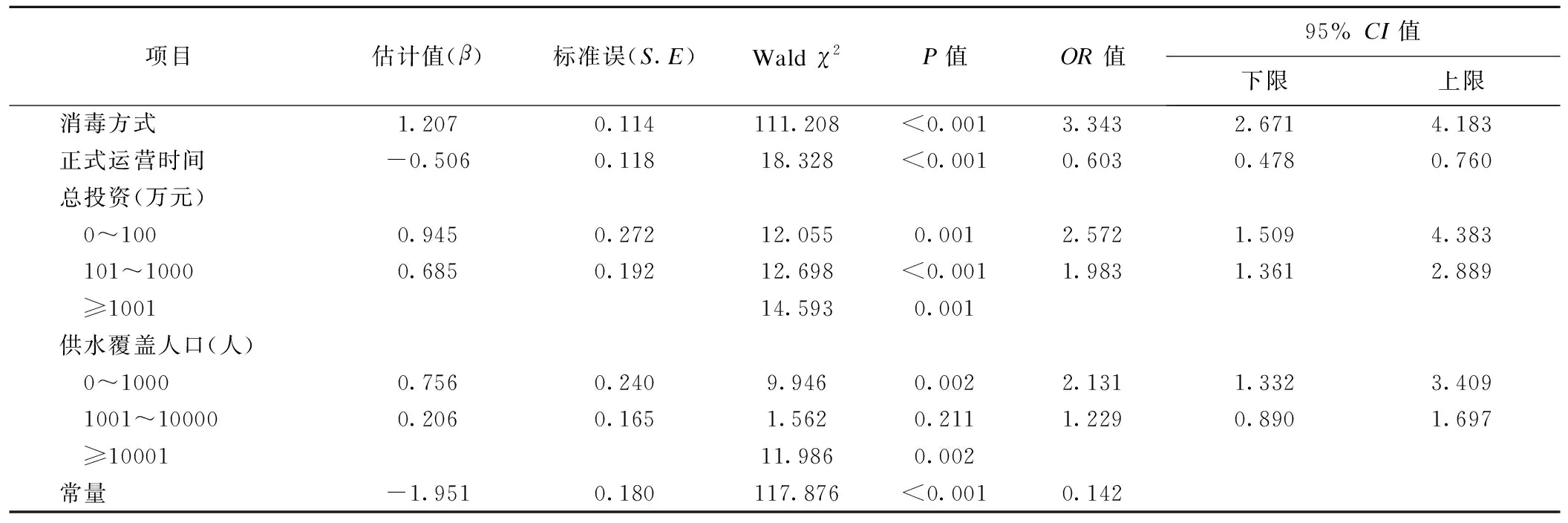
表3 饮用水水质结果和多因素logistic回归分析

2.单因素分析

单因素分析结果显示，消毒方式、监测点类型、正式运营时间、总投资、日供水能力、供水覆盖人口等6个自变量对水质结果的影响有统计学意义，将这6个自变量纳入logistic回归模型和CHAID模型中。水源类型、水期类型、卫生许可、水样类型共计4个自变量对水质结果的影响差异无统计学意义，予以排除，见表2。

3.多因素logistic回归分析

将影响水质结果的6个相关因素用最大似然估计的向前逐步回归法进行分析，在α进入=0.05，β剔除=0.10的条件下进行，通过回归模型检验χ2=239.352，P<0.001，表明回归方程有统计学意义，分析结果见表3。该模型错误分类率为27.8%，分类效果较好。由表3可见，有4个因素进入回归方程，渭南市生活饮用水水质受到消毒方式、正式运营时间、总投资、供水覆盖人口的影响(P<0.05)，监测点类型、日供水能力被剔除。其中消毒方式对水质的影响程度最大。通过分析得知工程不消毒、工程运营时间越长，水厂规模(总投资和供水覆盖人口)越小，水质不合格率越高。

4.决策树CHAID模型分析

如果在某节点不存在有统计学意义的进一步划分，则在此节点停止分支成为叶节点[5]。该决策树模型最大树深度为3，父节点为100，子节点为50，产生的终末决策树模型见图1。水源类型、水期类型、卫生许可、水样类型、日供水能力被剔除出该模型。

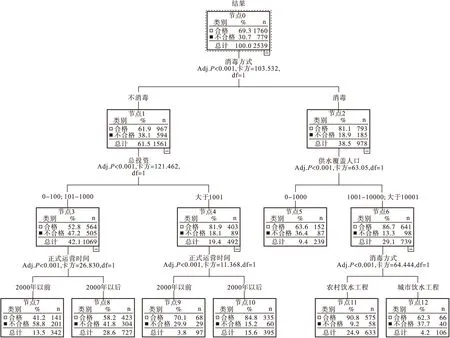
图1 CHAID方法对饮用水水质结果影响因素分析的分类树型图

通过分析得出决策树模型错误分类率28.3%，分类能力较好。影响水质结果的有消毒方式、总投资、供水覆盖人口、正式运营时间、监测点类型。决策树第一层为消毒方式，表明消毒方式与水质结果的相关性最高，消毒后水质合格率(81.1%)比不消毒的水质合格率(61.9%)高；在消毒饮水工程中供水覆盖人口大于1000人的工程水质合格率(86.7%)高于少于1000人的饮水工程(63.6%)。在大于1000人的供水工程中农村饮水工程水质合格率(90.8%)高于城市饮水水质合格率(62.3%)；在不消毒的饮水工程中总投资大于1000万的工程水质合格率(81.9%)高于总投资小于1000万的饮水工程水质合格率(52.8%)。在所有供水工程中运营时间越久的工程水质合格率越低。

5.两种模型预测能力评估

两种模型的分析结果显示，水源类型、水期类型、卫生许可、水样类型在两方法中均被排除，均显示此四种因素均不是水质结果的影响因素。logistic回归模型中的影响因素包括日供水能力，然而在决策树模型中被剔除。决策树类型中有监测点类型，而在logistic中被剔除，显示了两模型的不同之处。

logistic回归模型预测准确率为72.2%，灵敏度为64.83%，特异度为67.95%，约登指数32.8%，ROC曲线下面积为0.701(95%CI0.682～0.718)。决策树模型的预测准确率为71.7%，灵敏度为81.13%，特异度为55.57%，约登指数36.7%，ROC曲线下面积为0.725(95%CI 0.707～0.743)。决策树模型曲线下面积高于logistic回归模型，两个模型的ROC曲线下面积之间的差异有统计学意义(Z=3.623，P<0.001)。两模型的预测效果为中等(0.7～0.9)(图2)。

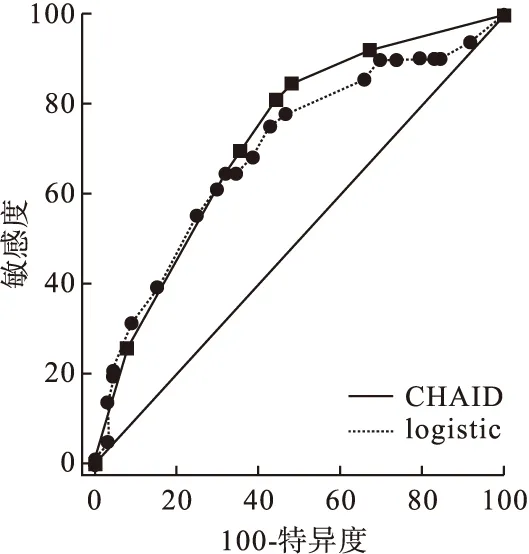
图2 logistic回归与CHAID模型的ROC曲线对比图

讨 论

决策树是一种通过树状图来表现数据受各变量影响情况的分类预测模型，不但可以筛选主要影响因素，还能清晰展示变量之间交互作用的功能，并可以根据对目标变量产生效应的不同而制定分类规则，它是建立在信息论基础之上对数据进行分类的一种方法[6]。从统计学角度来说，决策树属于非参数统计，其打破了传统的线性处理方式，消弥了变量间的共线性，避免了复杂参数估计来解释变量间关系而不能用函数表达的分类问题[7]。本文将决策树模型与多因素logistic回归模型互为补充，以此来充分解释变量间的关系。

本研究首次使用CHAID模型与logistic回归模型对2539份饮用水进行分析研究。通过研究发现应用logistic回归和决策树两种方法对水质相关因素进行分析，两种方法分析结果较一致，消毒和水厂规模为主要影响因素。在两种模型中消毒方式都是影响水质结果的首要因素，消毒后的水质合格率81.1%，远高于不消毒的水质合格率61.9%。可见消毒与否是影响水质的首要因素。由于农村条件参差不齐，部分农村集中式供水的消毒设备因经济因素无投资，考虑到消毒方式的重要影响，相关部门应将专项资金拨款用于进一步完善消毒设备配备及使用情况，购买消毒剂及设备、管道更新和配备，提高水质合格率。

在决策树CHAID模型的构建过程中，总投资、供水覆盖人口作为连续变量进入模型，软件自动将研究对象分割为两部分，总投资分为1000万内和超过1000万两个子群，说明以1000万为分割点；覆盖人口分为小于1000人和大于1000人，说明以1000人为分割点，这样能最大限度提高决策树模型信息增益率，实现分类效率最大化[8]。决策树模型的第二层显示，水厂规模(总投资和供水覆盖人口)越小，水质不合格率越高。在不消毒的供水工程中，总投资越小水质不合格率越高，其原因可能是总投资高的水厂规模大，各项设备设施和人员管理方面都比较规范，相对于大投资水厂，低投资水厂各方面比较欠缺，更容易导致水质不合格。在消毒供水工程中，供水覆盖人口越大，水厂规模就越大，水厂管理更规范，水质合格率就高。决策树模型的第三层显示，运营时间越久的工程水质合格率越低。调查中发现渭南市集中式供水工程制水工艺比较陈旧，供水管网老化，输水管网的管材以金属为主，管网腐蚀和金属析出现象严重，是造成水质微生物、金属等指标超标的一个重要原因[9]。大于1000人的消毒供水工程中，农村供水工程水质合格率高于城市供水工程。一个原因是城市饮水工程基数(样本)较少，导致水质合格率低；另一个原因可能是城市管网复杂、老化，施工或材料的问题加上使用时间过长，造成水质差。

logistic回归的优势是在分析水质的合格率与各自变量的依存关系时，是在控制其他变量的情况下来分析某种变量的作用，主要反应某变量的主效应，而在自变量对因变量变化关系方面的信息比决策树模型充分。但logistic回归在反应变量间的交互作用上不如决策树模型的效果好。而决策树模型表现出大量的交互作用后，却无法反映因素的主效应和叠加效应[10]，有研究表明[11-13]，在实际应用中应将两者结合，可以最大限度地发挥决策树与logistic回归两种模型的优越性；利用决策树的直观效果、易解释、生成部分分类规则的优点，结合logistic回归模型给出每个变量的参数估计值以及假设检验结果的优点[14]，通过logistic回归模型筛选主效应变量，再利用决策树模型进一步研究变量间的交互作用[15]。

在本项研究中两种预测模型的准确率均达到70%以上，模型效果较好。决策树模型的灵敏度、约登指数高于logistic回归预测模型；logistic回归预测模型的特异度、准确度高于决策树模型。ROC曲线一般位于机会线的上方，因此AUC在0.5到1之间，面积越接近1，说明模型的判别效果越好[16]。logistic回归模型ROC曲线下面积为0.701，决策树模型ROC曲线下面积为0.725。两模型比较Z值为3.623，P<0.001，表明二者差异有统计学意义，说明决策树模型的评价效能优于logistic回归预测模型。logistic回归和决策树的不同算法各有优势[17-18]，决策树模型灵敏度较高，logistic回归模型的特异度较高，两者结合，将更加有助于找出影响干预效果的因素[19]。

本研究纳入的影响水质合格率的个别变量结果无统计学意义，如水源类型、水期类型、卫生许可、水样类型未纳入预测模型。本文旨在为水质影响因素的研究提供新思路，水质好坏的影响因素众多，CHAID决策树模型在生活饮用水水质影响因素风险评估方面有较高的应用价值，其与logistic回归相结合应用，能够互相补充，从不同方面描述影响水质合格率的因素及作用，为进一步制定相关政策和方案提供依据和参考。