小波变换与CNN 相结合的视频加密算法

信阳农林学院 信息工程学院,河南 信阳464000

在通信技术和网络技术快速发展的同时，视频信息以其生动形象、视觉冲击力强等优点迅速成为人们进行交流的重要方式[1,2]。随着人们对其安全性的要求不断提高，视频加密算法的研究也已成为热点[3,4]。由于视频的数据量较大，传统的加密方法已经不能满足视频加密的需要，故基于混沌的加密算法不断被提出。文献[5]提出基于幻方变换的HEVC熵编码加密方案；文献[6]提出基于LCD模型的LCU选择性视频加密算法，此法针对于HEVC格式的视频，采用Arnold变换进行加密；文献[7]针对于H.264/AVC格式的视频，提出了基于量子细胞神经网络超混沌的视频加密方法。以上文献均基于特定的视频编码标准，具有一定的局限性。文献[8]提出基于细胞神经网络超混沌系统的视频加密方法，文献[9]提出基于混沌键控的视频加密方案，但文献[8]和文献[9]为了提高加密效率，舍弃了置乱加密过程，只保留了替代加密过程，

安全性能有所下降。文献[8,9]的算法虽然具有通用性，但加密后的视频文件数据量是原视频数据量的四倍，造成信息传输和存储的负担。因此，本文设计了小波变换与细胞神经网络相结合的视频加密方案。细胞神经网络的并行性和稳定性良好，易于超大规模集成电路实现，适合应用于视频加密系统中[10]。由于视频帧的大部分信息都集中在低频部分[11,12]，故该算法无论是置乱加密还是替代加密，都只针对于低频部分。优点是使需要处理的数据量和加密所需的超混沌值都大幅度减少，在克服高维超混沌系统产生密钥时间较长，不能满足视频加密实时性要求的同时，也使加密后的视频数据量变小，安全性和加解密效率有所提高。

1 细胞神经网络和小波变换

1.1 五维细胞神经网络超混沌系统

细胞神经网络Cellular Neural Network（简称CNN）的n阶动态模型如下[13,14]：

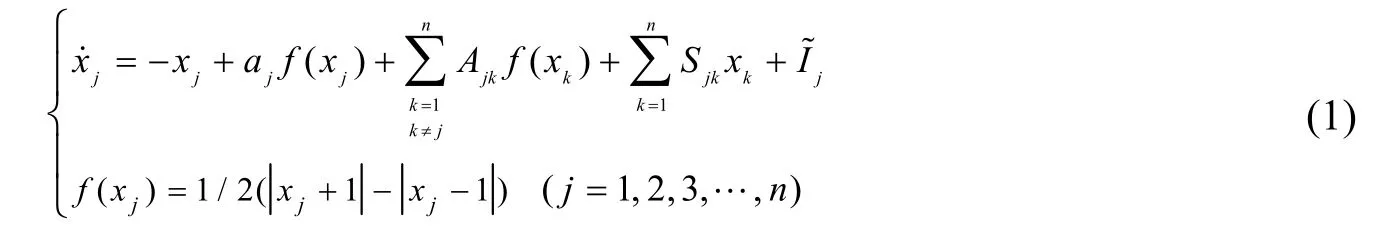
上式中j为细胞记号，aj、Ajk、Sjk和为细胞参数，f(xj)为细胞的输出。若n=5、S11、S23和S33为1，S13、S14、S45和S55为-1，S22为3，S31为11，S32为-12，S41为92，S44为-94，S53为15，a4为202，其余参数均为0 时，则五维CNN 超混沌系统的数学模型如式(2)所示：

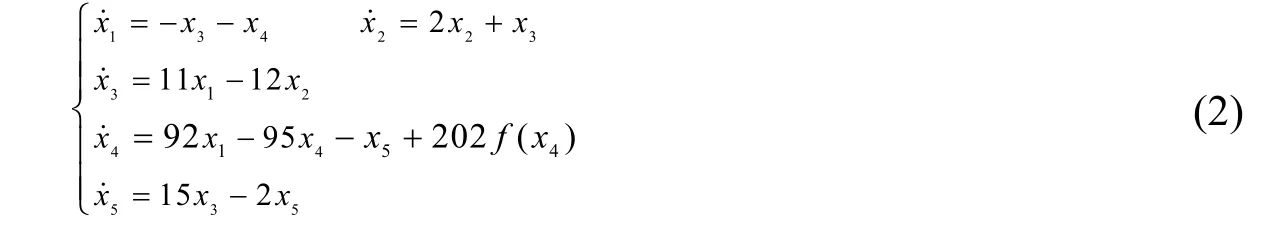
Lyapunov 指数是描述初始值受到微扰后混沌轨道的分离量，具有两个以上正Lyapunov 指数的系统是超混沌系统。上述五维CNN 系统的Lyapunov 指数分别为0.5285、0.1264、0.2953、-3.9205和-17.4382，有三个是正数，故该系统为超混沌系统。本文采用Matlab 2013 作为实验仿真平台，使用M 语言进行程序编写。当初始值x1(0)=0.1，其它初始值均取值0.2 时，使用四阶Runge-Kutta 算法求解式(2)，则五维CNN 系统x3、x4和x5序列所产生的超混沌吸引子如图1 所示。

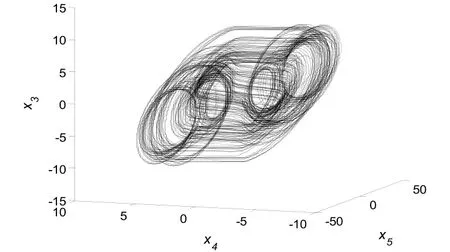
图1 五维CNN 系统x3,x4,x5 超混沌吸引子Fig.1 Hyper chaotic attractors for five-dimensional CNN systemsx3,x4,x5

使用密钥变化率KCR(Key Change Rate)对上述系统的初始值敏感性进行分析。KCR 的值越大，表示敏感性越强，反之越弱。初始值x1(0)=0.1，其它初始值均取值0.2。若将x1(0)的取值增加le-17，其它初始值不变，则五维CNN 系统的KCR 为0.9980；对其它初始值的KCR 进行测试，实验结果分别为0.9991，0.9993，0.9984，0.9981。从以上数据可以得出，五维CNN 超混沌系统对初始条件是极为敏感的，适合将其应用于视频加密系统中。

1.2 小波变换

小波变换的基本思想是用基本小波函数通过平移或拉伸得到的一族函数表示或逼近某一信号。可将原始视频帧图像进行二维离散小波变换，则二级小波变换过程如图2 所示。

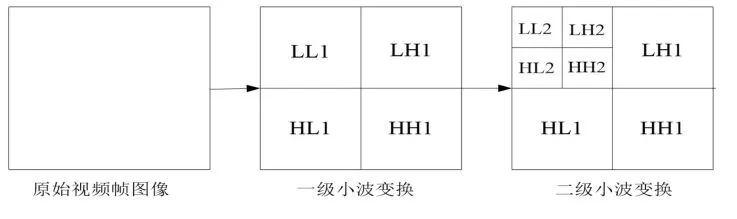
图2 二级小波变换Fig.2 Second-order wavelet transform

从图2 可以看出，原始视频帧图像经过第一次小波变换后，被分为LL1、LH1、HL1 和HH1。其中LL1 为低频分量，保存着原始视频帧图像的基本信息，是其主要能量的集中地；而LH1（水平方向）、HL1（垂直方向）和HH1（对角方向）为高频分量，保存着原始视频帧图像的边缘、轮廓等信息。二级小波变换是将LL1 再分为LL2、LH2、HL2 和HH2，三级小波变换是将LL2 再次分为LL3、LH3、HL3 和HH3，呈现出金字塔状的分解方式。小波变换结束后，视频帧图像的主要能量集中在最高的LL 分量中。

可使用Matlab 中的dwt2 函数对原始视频帧图像进行二维离散小波变换，idwt2 函数进行二维离散小波反变换。

2 加密算法描述

2.1 超混沌系统初始值的选取

选取初始值：

上式中的R、G和B分别表示明文视频帧所有像素的红色、绿色和蓝色分量的异或值，⊕为异或操作，ki为初始值调节参数，xi(0)为选取的初始值。

2.2 超混沌序列的处理

每1 路超混沌序列将产生P个值，P=Max(M,N)/2，M为视频帧的高，N为视频帧的宽，Max 取最大值。使用下列公式对超混沌序列进行处理，x(i,j)为最初生成的超混沌值，y(i,j)为经过处理后的超混沌值，fix为向0 靠近取整，abs为取绝对值操作。

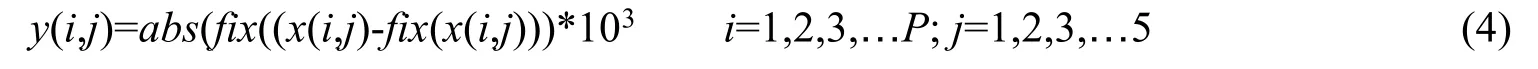
2.3 选择加密密钥

由公式(5)来决定加密密钥，选择Rank1和Rank2路超混沌值作为置乱加密密钥，Rank3、Rank4和Rank5路超混沌值作为像素替代加密密钥。其中VidXor为明文视频帧所有像素所有颜色分量的异或值，mod 为取余操作。

2.4 置乱加密

2.4.1 小波变换 将原始视频帧图像进行一级二维离散小波变换，取其低频部分信息，只对低频部分的数据进行处理。

2.4.2 行置乱 使第i行和第rowi行的数据互换位置。

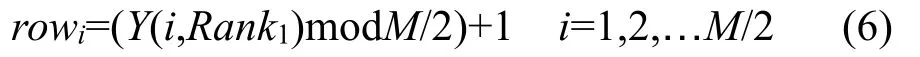
其中Y(i,Rank1)表示选取处理后的超混沌序列中第i行，第Rank1列的密钥值，Rank1的值由公式(5)计算得出。M为视频帧的高，mod 为取余操作。

2.4.3 列置乱 使第j列和第colj列的数据互换位置。

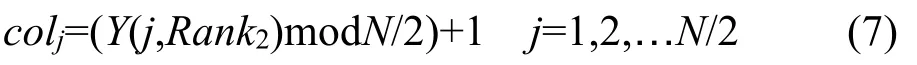
其中Y(j,Rank2)表示选取处理后的超混沌序列中第j行，第Rank2列的密钥值，Rank2的值由公式(5)计算得出。N为视频帧的宽，mod 为取余操作。

2.4.4 像素置乱 使像素(i,j)和像素(rowi,colj)互换位置。

公式(8)中的变量同公式(6)和公式(7)。

为了使置乱效果更好，可以将2.4.2～2.4.4 迭代k次，k可取任意的正整数。

2.4.5 像素替代加密 对于置乱后的加密视频帧，采用如下公式进行像素替代加密：

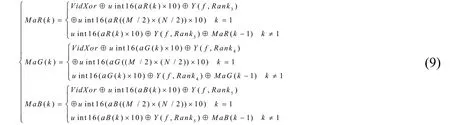
上式中的f=(i×j)modP+1，i和j分别为视频帧像素的行号和列号，P为每1 路超混沌序列产生的密钥数；Rank3、Rank4和Rank5的值由公式(5)计算得出；Y为加密密钥；uint16 将数据转换为16 位的无符号整数；aR(k)、aG(k)和aB(k)分别为置乱加密后第k个像素的红色、绿色和蓝色的值；MaR(k)、MaG(k)和MaB(k)分别为像素替代加密后第k个像素的红色、绿色和蓝色分量的值；VidXor为明文视频帧所有像素所有颜色分量的异或值；M为视频帧的高，N为视频帧的宽；⊕为异或操作；mod 为取余操作。

2.4.6 解密 解密过程是加密过程的逆过程。

3 仿真实验和性能分析

3.1 加解密效果分析

将由摄像头采集的视频信息存储到AVI 格式的视频文件中，采用上述算法对其进行加解密处理。初始值密钥调节参数k1、k2、k3、k4和k5分别取0.1、0.2、0.3、0.4 和0.5，小波基函数选取db1，则加密算法的部分代码如下：

图3 为视频的加解密效果，图3(a)为明文视频，图3(b)为加密后的视频，图3(c)为解密后的视频。

图3 视频的加解密效果Fig.3 Encryption and decryption effect of video

从图3 可以看出，在视觉感观上，加密后的视频与明文视频毫无关联，而解密后的视频与明文视频又并无差异，说明该视频加密算法的加解密效果良好。

3.2 敏感性分析

3.2.1 密钥敏感性 当解密的初始值密钥x′1(0)=x1(0)+10-16，其它密钥不变时，图3(d)为其解密视频。从图中可知，即使只有一个初始值密钥发生了微小变化，其解密结果也会完全错误。对其它初始值密钥进行测试，得到的实验结果类似。在5 个初始值密钥中，敏感性达到10-16的有3 个，达到10-15的有2 个。文献[15]和文献[16]的初始值密钥敏感性均为10-15。本算法的初始值密钥敏感性优于上述文献，具有良好的初始值密钥敏感性。对其它密钥的敏感性分析与此类似，不再赘述。

3.2.2 明文敏感性 使用NPCR（Number of Pixels Change Rate）和UACI(Unified Average Changing Intensity)对算法的明文敏感性进行分析。NPCR 的理想值约为0.996，UACI 的理想值约为0.333，表1 为明文敏感性的仿真实验结果。

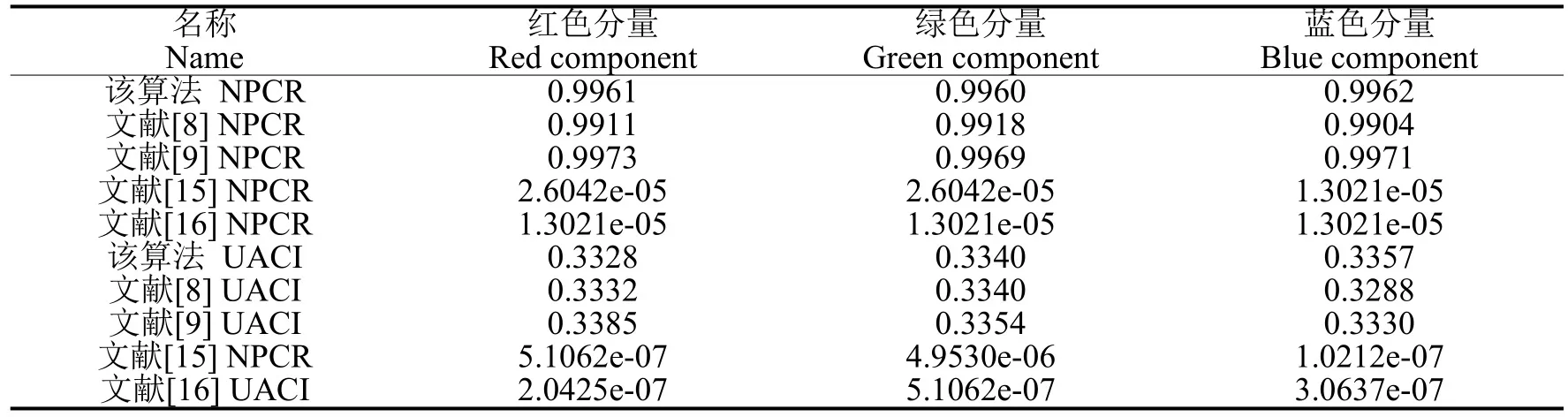
表1 明文敏感性NPCR 和UACI 的仿真实验结果Table 1 Simulation results of plaintext sensitivity NPCR and UACI

从表1 可知，文献[15]和文献[16]的NPCR 和UACI 值和理想值的差距较大，明文敏感性不强。而本算法NPCR 和UACI 的平均值分别为0.996 和0.334，比文献[8]和文献[9]更接近于理想值。仿真实验数据表明该算法的明文敏感性优于上述文献。

3.3 密钥空间分析

五维CNN 超混沌系统有55 个模板参数和5 个初始值，共计60 个密钥。采用16 位有效数字作为计算机浮点数的计算精度，则该算法的密钥空间为10960。另外5 个初始值调节参数密钥也使其密钥空间变得更大。文献[9]的密钥空间为10880，文献[15]的密钥空间为1032，文献[16]的密钥空间为10144，该算法的密钥空间比上述文献大，可有效地抵抗穷举攻击。

3.4 统计特性分析

3.4.1 直方图 图4(a)为明文红色分量的直方图，图4(b)为密文红色分量的直方图。

从图4 可以看出，明文视频帧的直方图呈现高低错落的山峰状，取值在200 左右的像素极少，取值在[220～255]的像素几乎没有；而密文视频帧的直方图则分布均匀，每个取值等级上的像素个数均在70 个左右，明文的统计特性被完全打破。

3.4.2 相关性 相关系数越接近于1 或-1，相关度越强；相关系数越接近于0，相关度越弱。相关系数在0.8～1.0 之间为极强相关；0.6～0.8 为强相关；0.4～0.6 为中等程度相关；0.2～0.4 为弱相关；0.0～0.2为极弱相关或无相关。表2 为明文视频和密文视频相邻像素相关性的仿真实验结果。

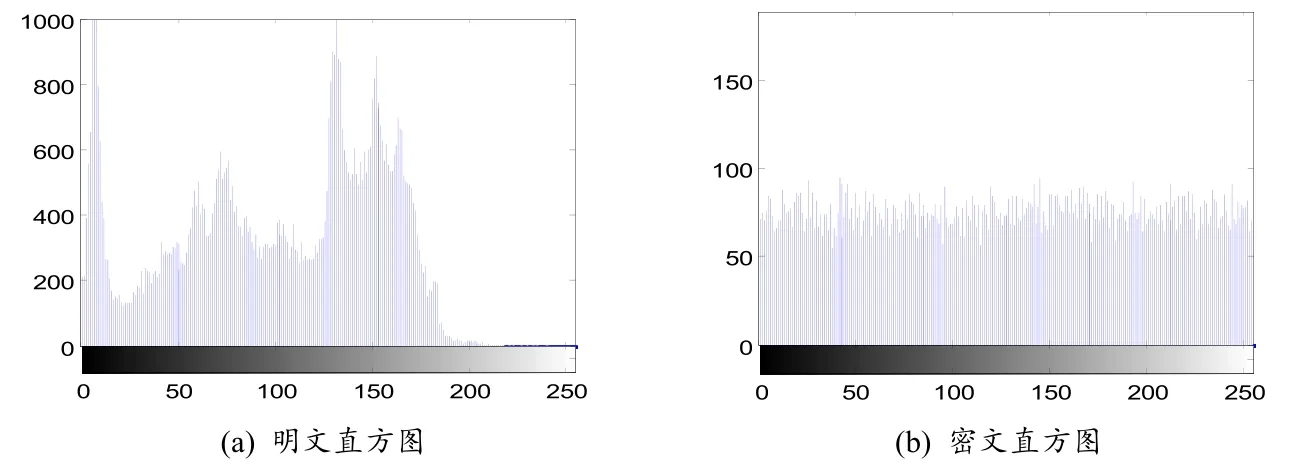
图4 红色分量直方图Fig.4 Red component histogram

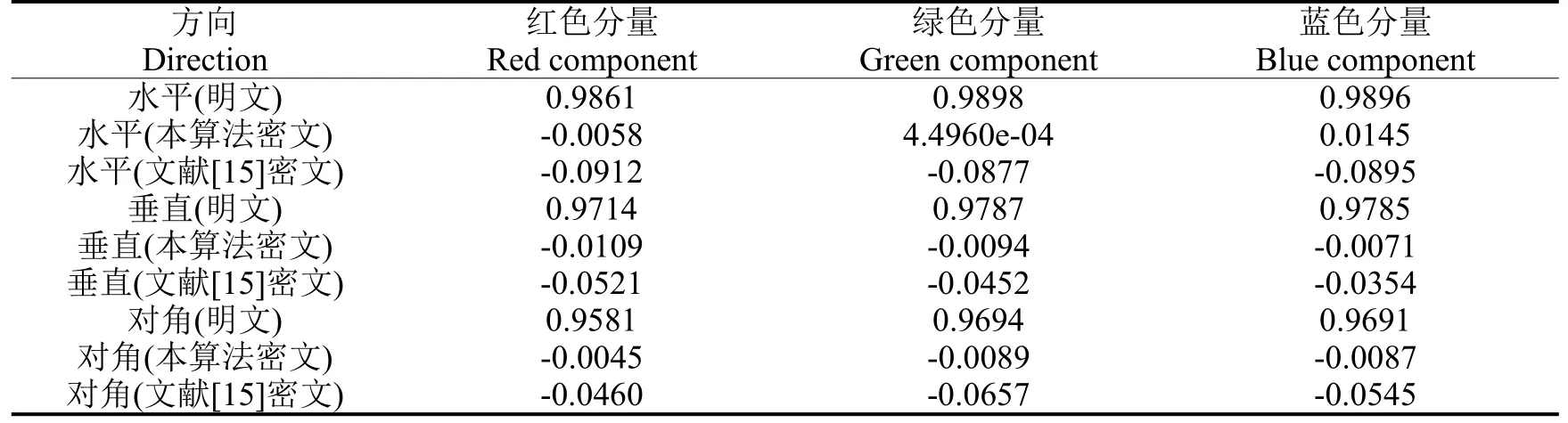
表2 相邻像素相关性的仿真实验结果Table 2 Simulation results of correlation between adjacent pixels

从表2 的实验数据可知，明文视频的相关性接近于1，相邻像素点之间为极强相关；而密文视频的相关性接近于0，相邻像素点之间为极弱相关或无相关。且该算法的9 个相关性值均比文献[15]小，其相关性方面优于文献[15]。

3.4.3 信息熵 密文视频帧信息熵的理想值为8，体现其分布的聚集特征。该算法密文在红色、绿色和蓝色分量上的信息熵分别为7.9862、7.9852 和7.9849，接近于理想值，而文献[15]的信息熵接近于7。由此可见，该算法在信息熵方面要优于文献[15]。

3.4.4 幅值频谱图 使用幅值频谱图来分析视频帧的频率分布情况。图5(a)为明文的二维幅值频谱图，图5(b)为密文的二维幅值频谱图，图5(c)为解密视频帧的二维幅值频谱图。

图5 二维幅值频谱分析Fig.5 Two-dimensional amplitude spectrum analysis

从图5 可以看出，明文的幅值频谱大多集中在中心区域，中心的亮点反映的是视频帧的低频信息。密文视频帧的幅值频谱在二维空间内分布比较均匀，离散化。可有效抵抗密文信息攻击，安全性较好。解密视频帧的幅值频谱与明文视频帧的高度相似，说明该加密算法的匹配度较高。

图6 抗噪性和抗剪裁性分析Fig.6 Anti-noise and anti-tailoring analysis

3.5 抗噪性和抗剪裁性分析

若密文视频受到噪声密度为0.01 的椒盐噪声影响，则解密视频如图6(a)所示；若密文视频受到了左上角1/4 的剪裁攻击，则受剪裁攻击的密文视频如图6(b)所示，解密视频如图6(c)所示。

从图6 可以看出，虽然受到了噪声影响或剪裁攻击，该算法仍能有效地解密视频信息。仿真实验结果表明，对于噪声影响的抵抗性，椒盐噪声最优，其次是乘性噪声，最后是高斯白噪声。

3.6 加密后的视频大小和加解密速度

由于视频信息的数据量相当大，且某些场合对实时性的要求又较高，故加密后视频文件的大小以及加解密速度，也是衡量加密算法性能优劣的重要指标。使用处理器为AMD A8-4500 M APU with Radeon™HD Graphics 1.90 GHZ，内存为4 GB 的计算机，对加密后的视频大小和加解密速度进行分析。原视频为367 kb，该算法加密后的视频为425 kb，文献[8]为1436 kb，文献[9]为1435 kb。从以上仿真实验数据可知，文献[8]和文献[9]加密后的视频比原视频的数据量大了很多，这会造成传输和存储的负担。故性能优良的算法应该使加密后的视频数据量尽量地小，该算法在此性能方面要优于文献[8,9]。为了节省加解密时间，文献[8]和文献[9]舍弃了置乱加密过程，只保留了替代加密过程。为了提高算法的安全性，该算法同时保留了置乱加密过程和替代加密过程，平均每帧的加密时间约为0.6331 s，解密时间约为0.7454 s，有效地平衡了视频加密算法对安全性和实时性的需求。

4 结论

本文提出了小波变换和CNN 相结合的视频加密算法，并从加密效果、敏感性、密钥空间、统计特性、抗噪性、抗剪裁性、加密后视频大小和加解密速度等方面进行了性能分析。仿真实验结果表明，该加密算法在提高其安全性的同时，有效地减少了加密后视频的数据量，并提升了加解密效率，应用价值较高。