基于双层优化和态势感知的智能配电网精细化日前优化调度

孙晓艳

1.无锡职业技术学院,江苏 无锡214121

2.江苏大学无锡机电学院,江苏 无锡214121

随着传统配电网逐渐向智能配电网（Smart Distribution Grids，SDG）过渡，高级自动化和大数据技术等新技术的快速发展和应用为配电网实现源-网-荷各侧资源的综合协调优化运行提供了条件[1,2]，但同时以风机、光伏为代表具有强不确定性的分布式可再生电源(Distributed Renewable Generation，DRG)并网比例的显著提高，将导致弃风弃光等问题，甚至可能威胁到配电网的安全运行[3,4]，传统的配电网调度运行方法不再适用。

目前国内外学者已开展了大量研究和实践工作。文献[5]通过对可控光伏实现有功无功解耦控制，以配电网企业运行成本最小为目标，建立了有功无功协调优化的日前调度模型；文献[6]分析了DRG并网对智能电网的影响，并以DRG 并网后的系统运行网损最小为目标，建立了日前调度模型；文献[7]基于二层规划和机会约束规划建立网络结构和DRG 有功出力的协调调度模型，应用遵循解环原则的遗传算法对其求解，但未计及储能和柔性负荷等可控资源；文献[8]计及风电出力不确定性提出了综合考虑备用市场成本、电力交易成本和运行成本的优化调度模型；文献[9]计及了DRG、储能和柔性负荷等可控资源对配电网进行多目标优化调度，其中文献[10]建立了调度周期内以DRG 利用率最大、网损最小和用户满意度最高为目标的日前调度模型，并采用层次分析-熵权法确定各子目标权重系数，但层次分析法是一个主观定权方法，在确定权重系数时仍需主观判断并受其影响；文献[11]建立了以DRG 有功削减量、系统运行成本和网损三方面最小为优化目标的多目标日前调度模型，应用多目标和声搜索算法求解得到Pareto 前沿并采用逼近理想解排序法得到最佳折中方案，但仍需人为确定不同目标的权重来确定最佳方案。

1 基于自适应变权重的SDG 精细化综合日前调度模型

1.1 目标函数

式中：RtV、RtDRG和RtC分别为SDG 在t时段的系统电压裕度、DRG 出力削减率和运行成本率，wtv、wtdrg和wtc分别是相应指标在t时段的权重因子。

式中：RtV,t和Vti分别为配电网t时段第i个节点的电压裕度和节点电压幅值，当RtV,t≤1 时，节点电压未越限，当RtV,t＞1 时，节点电压越限，且RtV,t越大，节点i电压越限越严重；VN为全网统一的额定电压；Vmax和Vmin分别为节点电压幅值的上、下限；N为配电网节点电压总个数。

式中：Ndrg为DRG 的总台数；为第i台DRG 在t时段运行环境下的最大可能出力，该出力由该时段的风光气象数据结合具体的风机或光伏的数学模型计算得到[9]；为该DRG 所要削减的出力。

式中：Ctdeal为t时段配电网与上级电网的交易成本，αtdeal为配电网与上级电网间的购售电标识变量，从上级电网处购电时αtdeal=1，向上级电网售电时αtdeal=-1，ctgrid为t时段配电网与上级电网的交易电价，Ptgrid为该时段配电网与上级电网的交互功率，ΔT为时段间隔；Ctloss为t时段配电网的损耗成本，由网络损耗成本Ctloss,net和储能损耗成本Ctloss,ess组成，ctloss为t时段损耗成本电价，Ptloss,net为t时段配电网的网络损耗功率，Ness为储能总个数，Ptess,i和ηess,i分别为第i个储能的充放电功率和充放电效率，ηess,i可以分别为充电效率ηiness,i和放电效率ηoutess,i，当储能充电时，Ptess,i＜0，ηess,i为充电效率ηiness,i，放电时Ptess,i＞0，ηess,i为放电效率ηoutess,i；Ctdrg为t时段配电网向DRG 购电的成本，ctdrg,i和Ptdrg,i分别为t时段第i台DRG 的上网电价和实际出力；Ctdms为t时段配电网的柔性负荷调节成本，由负荷削减成Ctcut和负荷平移成本Cttran构成，Ncut为参与负荷削减的总用户数，ctcut为负荷削减的用户补偿电价，Ptcut,i为t时段第i个用户的负荷削减量，Ntran为参与负荷平移的负荷节点数，cttran为负荷每平移一个时段的用户补偿电价，Pttranout,i和ΔDttran,i分别为t时段第i个用户的负荷平移移出量和负荷平移时段数。

1.2 约束条件

式中：式(11)为配电网的功率平衡约束；式(12)为节点电压上下限约束；式(13)为支路功率上限约束；

式中：式(14)为网络拓扑约束；式(15-16)为开关操作次数约束。

式中：式(17-19)分别是DRG 的有功出力上下限约束、功率因数调节上下限约束和有功出力削减约束。

式中：式(20-23)分别为储能的逆变器容量限制、充放电功率上下限约束、荷电状态及其上下限约束。

Qtsc,i为第i台STATCOM 在t时段的无功出力，Qsc,i,min和Qsc,i,max为其出力上下限。

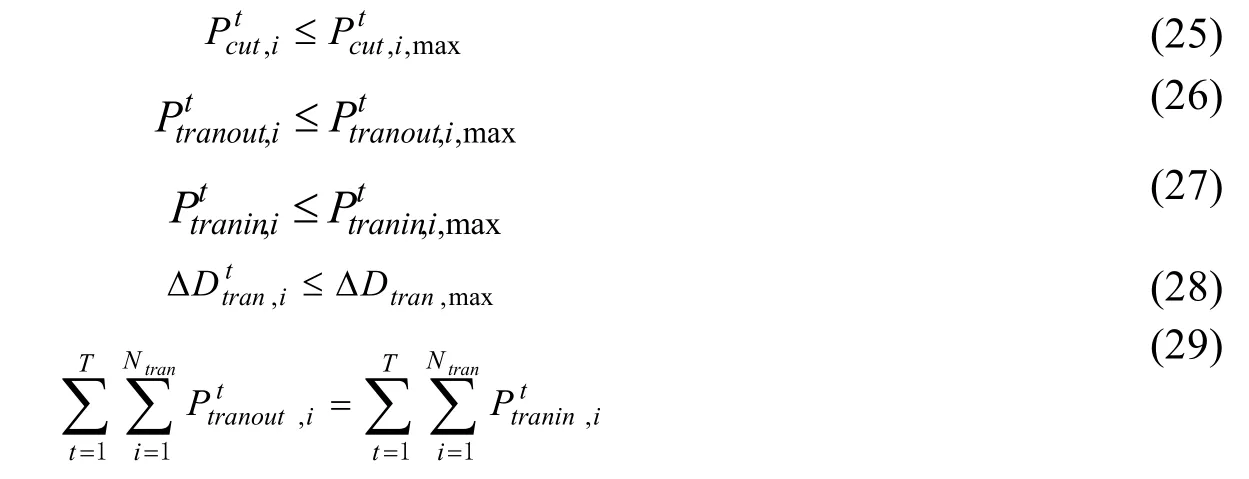
式中：柔性负荷可分为可削减负荷和可平移负荷，式(25)为可削减负荷的削减量上限，式(26-29)分别为可平移负荷的移出量上限、移入量上限、最大延迟供电时间约束和平衡约束。

2 基于双层优化策略的调度模型求解

如图1 所示为基于双层优化策略的调度模型求解流程图，其寻优流程如图2 所示。

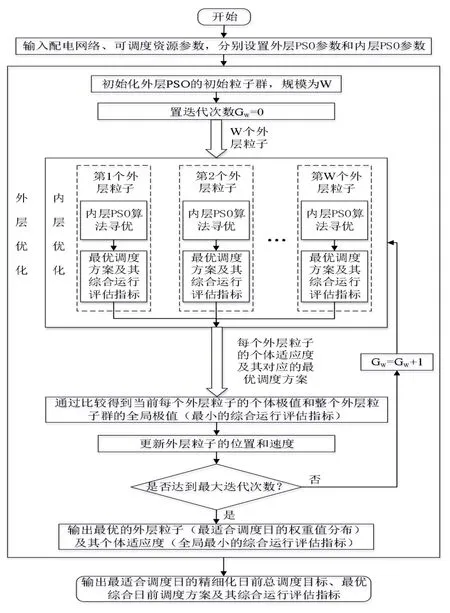
图1 基于双层优化策略的调度模型求解流程图Fig.1 Flow chart of solving scheduling model based on bilevel optimization strategy

图2 内层PSO 算法寻优流程图Fig.2 Flow chart of inner layer PSO algorithm optimization

3 算例与分析

本文采用改进的IEEE33 节点配电系统[12]仿真，如图3 所示，并网电气设备的基本参数如下：节点22-32 的负荷参与柔性负荷调节，其可削减负荷比例为10%，可平移负荷比例为30%，最大允许延迟供电时间取6 h；风机安装在节点15 和26 上，额定容量分别0.8 MW 和0.2 MW；光伏安装在节点9、19、23 和32 上，其中32 节点的光伏的额定容量为0.8 MW，其余光伏的额定容量为0.2 MW；相同型号的储能安装在节点15 和32 上，其额定容量为1.4 MW，逆变器的最大视在功率为0.7 MW，SOC 调节范围为10%～90%；充放电效率为95%；STATCOM 安装在节点8，其额定容量为0.2 Mvar。

图3 改进的IEEE33 节点配电系统网络结构Fig.3 Improved network structure of IEEE33 node distribution system

调度日各个时段的光照强度和风速预测曲线如图4 所示，负荷预测曲线如图5 所示。

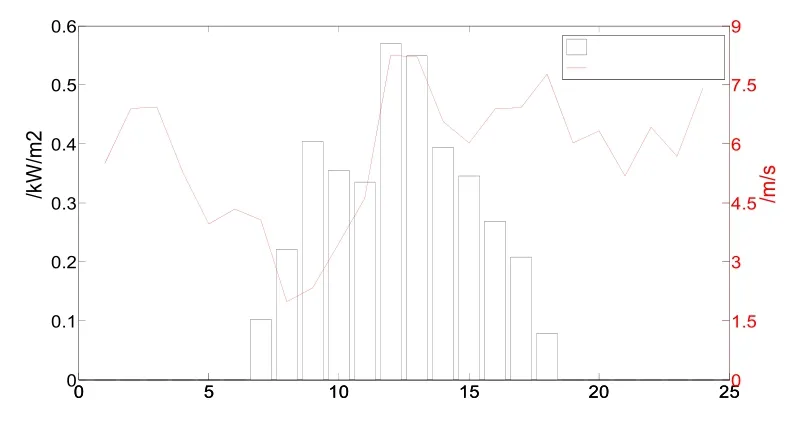
图4 调度日光照强度和风速预测曲线Fig.4 Forecasting curve of illumination intensity and wind speed on scheduling days

图5 调度日负荷预测曲线Fig.5 Forecasting curve of load on scheduling days

各时段配电网与上级电网的交易电价、损耗成本电价和负荷削减的用户补偿电价均取0.74 元/kWh，负荷每平移一个时段的用户补偿电价取0.12 元/kWh，风电和光伏的上网电价分别取0.80 元/kWh 和1.00 元/kWh[8]。系统电压裕度、DRG 出力削减率和运行成本率在各个时段的最终权重值如图6 所示。

图6 方案3 中各运行评估指标在各时段的权重值Fig.6 The weight value of each evaluation index in each period in scheme3

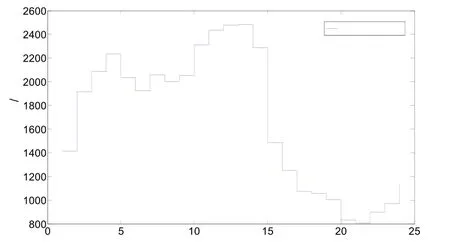
图7 基准调度方案在各时段的运行成本Fig.7 The operation cost of the benchmark scheduling scheme in each period

由图6 可知：系统电压裕度在1-9 和12 时段的权重值为0，说明调度日内配电网在这段时间不需要考虑运行安全问题，而在其他时段特别是负荷高峰期，配电网容易出现电压越限问题，故系统电压裕度权重值较高；DRG 出力削减率在负荷高峰期18-23 时段权重值为0，说明这段时间的运行环境，配电网均可满额消纳已并网DRG 的出力，只需保证配电网运行安全性和经济性即可，而在6-17 时段的权重值较高，这是由于这段时间的DRG 出力较大，这表明要在调度日的这段时间着重考虑如何减少弃风弃光；运行成本率的权重值在0-5 时段较高，甚至在2 和4-5 时段的权重为1，表明此时配电网既难以出现电压越限问题，也难以出现弃风弃光问题，调度时重点关注经济性即可。

为充分验证本文所提方法和模型的优越性，本文针对上述算例采用了以下四种方案分别进行优化调度并比较分析其调度结果。方案1：第1.2 节所提的基准调度方案，即不采取任何调度手段；方案2：以整个调度周期的运行成本率RtC之和最小为目标进行优化调度，即系统电压裕度RtV和DRG出力削减率Rtrdg在各时段的权重值均为0；方案3：利用本文所提考虑运行环境时变性的智能配电网精细化日前综合优化调度方法来进行优化调度；方案4：以调度周期的系统电压裕度、DRG 出力削减率和运行成本率之和最小为目标进行优化调度，其中上述三个运行评估指标在各时段的权重均各为1/3。方案1 在每个时段的运行成本如图8 所示，总运行成本为40225.77 元，由于方案1 是基准调度方案，则其每个时段的运行成本率RtC为1。四种方案的调度结果如表1 所示，四种方案在调度日的系统电压裕度、DRG 出力削减率和运行成本率如图9～11 所示，其中图9 内的左侧小图为纵坐标系统电压裕度在区间0-1 时的局部放大图。

表1 四种方案的调度结果比较Table 1 Scheduling results comparison of four schemes

观察表1 和图4～7 中四种方案的各类评估指标，可知尽管方案1(不调度方案)可使DRG 出力削减率为0，但却会造成SDG 在19-22 时段的电压严重越限，日系统电压裕度高达82.464，不满足配电网安全运行要求；比较方案2、方案3 和方案4 的各类评估指标可知：在运行安全性上，方案3的日系统电压裕度最低，优于方案2 和4，分别降低了1.412 和0.102，可以看出相较于方案2，方案3 的运行安全有明显改善，且由图7 可得方案3 和4 在各时段的RtV普遍低于0.5，安全裕度较高，而方案2 在时段17、21 和23 的RtV接近于1，表明这三个时段的配电网安全裕度较低，若在日内实际运行中存在突发情况，较大可能会发生电压越限，存在一定的安全风险；在DRG 消纳能力上，方案3 的日DRG 出力削减率最低，明显优于方案2 和4，分别降低了4.263 和3.401，结合图7 和图10 可发现正是因为方案3 在6-17 时段侧重优化Rtrdg这一指标，才使得方案3 在这段时间的Rtrdg较低；在运行经济性上，方案2 的日运行成本率最低，仅略优于方案3 和4，相较于方案3 和4 分别降低了0.337 和0.547；在综合运行评估指标上，方案4 劣于方案3，高出1.826。

4 结论

本文提出基于运行环境时变性的精细化综合日前调度方法。算例仿真结果表明：1）本文提出的精细化综合日前调度模型和方法能够根据每个时段不同的运行环境确定每个时段应该优化的侧重点，从而得到最适合调度日的目标函数。2）本文提出的基于双层优化策略的调度模型求解流程可以有效求解含有不止一类互相影响的控制变量的调度模型，进而得到既能有效提高配电网安全裕度，又能减少弃风弃光量，还能降低运行成本的最适合调度日的综合日前调度方案。