钢筋混凝土空腹夹层板楼盖结构的新型实用计算方法

安阳职业技术学院建筑工程系,河南 安阳455000

钢筋混凝土空腹夹层板结构[1]是一种新型的楼盖结构，它的出现使建筑结构体系形式更加的新颖多样。该楼盖结构高度低、整体刚度大、自由划分室内空间、节约层高、空腹夹层内可以走管线以及设置喷淋等优点。空腹夹层板有正交正放、正交斜放以及三向受力形式，目前，空腹夹层板楼盖也大面积应用于实际工程，比如贵州省兴义市党校礼堂、吉林省政协礼堂和青海省西宁市劳动局等。钢筋混凝土空腹夹层板楼盖结构的施工方式有装配整体式施工和现场浇制成型的施工方法。现场浇制可以分为现场二次浇制和现场一次浇制，该方法可以提高结构的整体刚度；装配整体式施工可以在保证刚度的基础上提高施工速度，节约工期[2]。

目前，国内外现有许多结构设计和结构分析软件。设计软件在分析钢筋混凝土空腹夹层板时对楼层的要求较高从而导致计算无法运行；结构分析软件可以建立真实模型分析而后处理相对麻烦[3-5]。钢筋混凝土空腹夹层板的常用分析方法有连续化分析方法、离散化分析方法以及实用分析方法，其中实用分析方法主要是等效刚度法[6]，本文在该方法的基础上提出另外一种等效方法—等挠度法，旨在完善相关的理论，为相应的设计提供一些有价值的参考。

1 实用分析方法—等效刚度法

等效刚度法将空腹夹层板看作空腹梁交叉组成，分析时考虑剪切变形的影响，基本假定如下[2]：

1)交叉的空腹梁上下肋变形后保持平面；

2)正交网格短边数目大于5 个，保证板网格的力学性能；

3)按照抗弯刚度等效原则；

4)空腹夹层板挠度验算时，考虑空腹板剪切变形、混凝土收缩等因素的不利影响，再考虑上板不参加工作的有利影响，计算所得的弹性挠度除以0.65 作为空腹夹层板楼盖的最大计算挠度。

等效刚度法是保持空腹夹层板的高度不变，按照抗弯刚度等效的原则进行等代，将空腹夹层板等代为实腹梁，然后利用PKPM 等软件进行分析，是目前空腹夹层板楼盖分析计算最常用的方法。等代模型如图1 所示，设空腹梁与实腹梁高度h相等，等代的实腹梁宽为：

图1 等效刚度法模型Fig.1 Equivalent stiffness method model

2 等挠度法

等挠度法则是采用相同的梁宽度，相同荷载，相同跨度的情况下，保持空腹梁与实腹梁有相等的跨中最大挠度，从而确定等效实腹梁的梁高。基本假定如下[7-9]：

1)板上下肋变形后保持平面，材料在弹性范围内；

2)网格短边数目不小于5 个；

3)其他方向对空腹梁相互作用的影响，并且荷载简化为均布荷载；

4)剪力键与上下肋均视为梁单元，并且考虑轴力和剪切变形的影响。

如图2 和图3 所示，图2 为n跨的空腹夹层板，每一跨的长度为a，上下肋的宽度和高度为b和h0，剪力键的截面尺寸为b×b，空腹夹层板的总高度为H。图3 为相同跨度的实腹梁，梁的宽度为b，高度为h1。两个模型所受的均布荷载相同的条件下，当空腹梁在荷载作用下的挠度一定时，实腹梁总有唯一的高度h1与其对应。

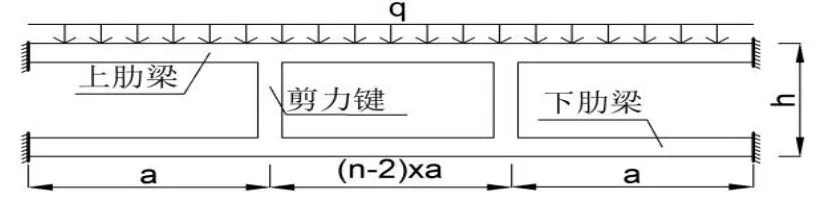
图2 空腹梁模型Fig.2 Hollow beam model

2.1 空腹梁单元刚度矩阵以及求解

由于剪力键短而粗，因此轴向力和剪切变形不能忽略。由有限单元法理论可知，考虑轴向力和剪切变形时梁单元在局部坐标的刚度矩阵[k]e见式(2)，整体坐标与单元坐标的转换矩阵[T]见公式(3)。

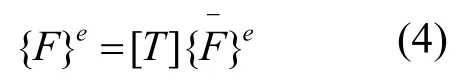
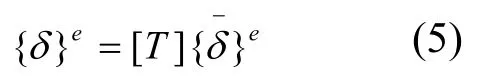
由结构力学知识不难得到每个节点的三个平衡方程见公式（6），总刚度矩阵公式（7）。

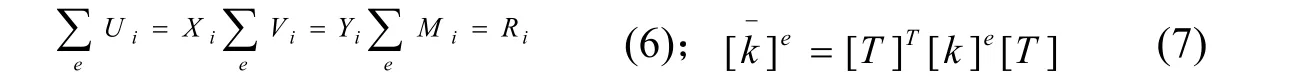
其中Xi Yi Ri均为作用于节点i的荷载；为环绕结点i的单元求和，总方程[10]为：

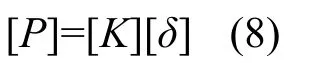
对于方程的求解以及内力的分配，手算则比较麻烦，因此可以利用通用有限元软件ANSYA 等求解，并且得到对应荷载下的挠度w0。

2.2 实腹梁单元相对应高度h1 求解

图3 实腹梁的边界条件做简化如图4 所示。

图4 实腹梁简化模型Fig.4 Simplified model of solid web beam

由材料力学知识可知，在材料在线弹性范围内，结构的位移与加载顺序无关[11]，因此在均布荷载q作用下简支梁的挠度，在弯矩M作用下简支梁的挠度为：

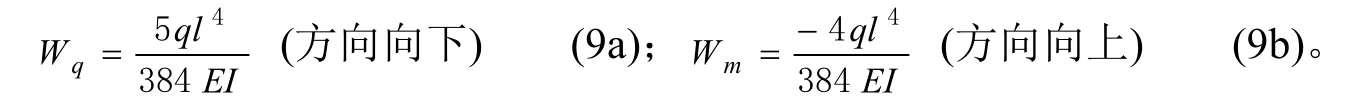
2.3 分析实例1

取空腹夹层板上肋和下肋的宽度b=0.3 m，高度h=0.2 m，剪力键尺寸为0.3 m×0.3 m，空腹夹层板高为h=0.55 m，单元长度a=2 m，跨数取6 跨，总长度为l=12 m；实腹梁跨度为l=12 m，宽度为b=0.3 m。材料弹性模量取2.06e10，泊松比为0.2，由于挠度Wo与均布荷载q成正比，为了使变形更加突出，取q=100 kN/m。

空腹梁在荷载作用下用ANSYS[12,13]所求得的挠度和内力图如图5 所示：

图5 空腹梁挠度与内力图Fig.5 Open web beam deflection and internal force diagram

由图5（a）可知，空腹的结构竖向位移为0.160 m；根据图5（c）轴力图可知，剪力键传递轴力并且轴力最大；根据图5（b）可知，靠近支座处的剪力键剪力最大，由支座向跨中的剪力键剪力逐渐减小，在设计时应该注重对剪力键的设计；由5（d）弯矩图可知，空腹梁的弯矩图较为复杂，剪力键与上下肋连接的地方可以设置成牛腿的形状进行加强。

由公式（10）可得等代的实腹梁高度h1=0.403 m，实腹梁位移图如6 所示，挠度为0.162 m，相对误差为1.24%，满足工程误差要求。

图6 实腹梁挠度图Fig.6 Deflection diagram of solid web beam

3 平面模型验证

3.1 上肋和下肋高度改变时的挠度分析

取空腹夹层板的上下肋高度变化从0.15 m 到0.25 m，跨数取3 跨，每次增加0.01 m，其它参数与实例1 相同。相同挠度时实腹梁的梁高h1如表1 所示，实腹梁对应的挠度以及误差如图7 所示。

表1 上下肋变化时实腹梁高度Table 1 Height of solid web beam as upper and lower ribs changing

图7 上下肋变化时挠度分析Fig.7 Deflection analysis as the upper and lower ribs changing

由图7 可知，空腹梁与实腹梁随着高度的增加挠度逐渐减小，变化趋势一致；实腹梁的挠度略大，但是最大误差不超过2%，同时小于5%，较好满足工程误差要求。

3.2 单元跨数改变时的挠度分析

保持单元长度a=2 m 不变，跨数变化范围3～15，梁的长度变化范围6 m～30 m，其它参数保持不变，其它参数与实例1 相同。相同挠度时实腹梁的梁高h1如表2 所示，实腹梁对应的挠度以及误差如图8 所示。

表2 跨数变化时实腹梁高度Table 2 Height of solid web beam as span number changing

由图8 可知，空腹梁与实腹梁随着单元跨数的增加挠度逐渐增大，两条曲线基本重合，说明挠度一致，最大误差不超过2%。

图8 跨数变化时挠度分析Fig.8 Deflection analysis as span number changing

3.3 单元长度改变时的挠度分析

保持梁的长度l=18 m 不变，单元长度发生变化，跨数随之变化，其它参数保持不变。相同挠度时实腹梁的梁高h1如表3 所示，实腹梁对应的挠度以及误差如图9 所示。

表3 单元长度变化时实腹梁高度Table 3 The height of the solid web beam as the length of the element changing

由图9 可知，单元跨度变化，总长度保持不变的情况下，空腹梁与实腹梁随着高度的增加挠度逐渐增大，最大误差在1%到2%之间。

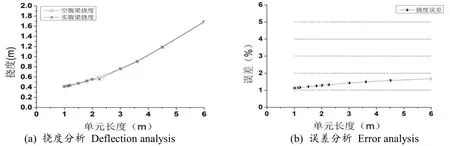
图9 单元长度变化时挠度分析Fig.9 Deflection analysis as element length changing

3.4 空腹高度改变时的挠度分析

保持其它参数保持不变，跨度18 m，单元长度2 m。改变空腹夹层板梁高度从0.460 m～0.600 m时，相同挠度下实腹梁的梁高h1如表4 所示，实腹梁对应的挠度以及误差如图10 所示。

表4 空腹夹层板高度变化时实腹梁高度Table 4 The height of the solid web beam as the height of the empty web sandwich panel changing

由图10 可知，空腹梁随着夹层板高度的增加挠度逐渐减小，因为空腹高度变高，增大了对形心轴的惯性矩，从而增大了空腹梁的抗弯刚度；与实腹梁的挠度误差最大值不超过2%，满足误差要求。

图10 空腹夹层板高度变化时挠度分析Fig.10 Deflection analysis of open-web sandwich panel as the height changing

4 等挠度法的空间模型验证

为了进一步验证该方法的可靠性，在平面模型验证满足要求的基础上，建立空间模型进行分析，分析时保证空腹梁与实腹梁结构截面的宽度和跨度相等，支座为固定端支座。取单眼长度为2 m，跨数从3 跨到9 跨，其他参数同实例一，计算所得实腹梁的高度结果同表2，挠度与误差如图11。

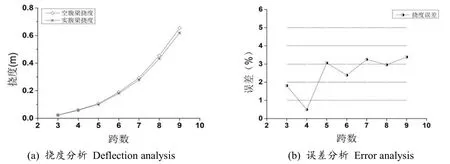
图11 跨数变化时挠度分析Fig.11 Deflection analysis as span number changing

由图11 可知，空间结构模型中，空腹梁和实腹梁挠度变化趋于一致，空间模型的挠度比平面模型的略大；空间空腹梁模型与实腹梁相比，挠度误差小于5%，同样满足工程误差需求，说明该方法也适用于空间模型。

5 等挠度法其他参数分析

5.1 楼盖高度分析

对于建筑楼盖来说，除了考虑楼盖的结构高度外，还应该考虑建筑的装饰高度以及房屋的使用净高。通过表1～4 可知，实腹梁的等代高度虽比空腹梁低，但是在实际工程中，房屋建筑的吊顶高度不能忽略。空腹夹层板楼盖的空腹可以走管线，设置喷淋等设备，不需要额外的层高进行装饰和吊顶；而等效实腹梁虽然高度低，但是需要进行额外的高度进行吊顶装修。随着技术的进步，大跨度结构越来越满足人们的需求，中间不设置柱子，空间网格可以自由划分[14,15]。

假定吊顶的高度为0.15 m，由表1～4 数据可知，空腹梁与实腹梁挠度相同时，实腹梁组成的建筑物楼盖高度h2=h1+0.15，与比空腹夹层板结构相比，跨度越大，所需要的高度h2就越大，因此在大跨度结构中，使用空腹夹层板楼盖可以有效节约层高，在一定程度上也可以节约额外的装饰吊顶费用，节约经济。

5.2 楼盖钢筋混凝土体积用量分析

钢筋混凝土的用量直接决定建筑物结构的经济成本，因此在分析时，应该考虑结构的混凝土用量。跨度和单元是影响混凝土用量的直接因素，在保证挠度相同和其他参数相同的情况下，分析不同跨度时，空腹夹层板与实腹梁混凝土用量随跨度的变化如图12 所示；保证跨度相同时，取不同的跨数，改变跨度所求得的混凝土用量如图13 所示。

图12 跨度变化时混凝土用量Fig.12 Concrete consumption as the span changing

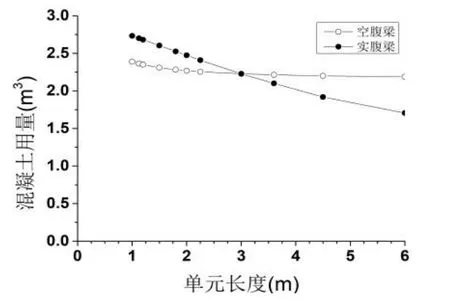
图13 单元长度变化时混凝土用量Fig.13 Concrete consumption as unit length changing

由图12 可知，单元长度一定为2 m 时，当跨度小于14 m 时，等挠度法所求得的实腹梁混凝土用量小于空腹梁；当14 m 跨度时，空腹梁与实腹梁钢筋混凝土用量相同，大于14 m 时，空腹梁的混凝土用量开始小于实腹梁，经济性开始凸显。由图13 可知，保持跨度为18 m 时，不同的单元长度对混凝土的用量有不同的影响。单元跨度在小于3 m 时，等挠度法所求得的空腹梁的混凝土用量小于实腹梁；大于3 m 时，实腹梁的混凝土用量较少。因此，设计时要选取合适的单元长度和跨度。

6 结论

1）通过对等挠度法的推导与验证可知，该方法有一定的理论依据，所验证的平面和空间模型误差均在5%以内，求得的结果满足理论与工程误差要求，说明该方法可以使用；

2）通过对层高和钢筋混凝土用量指标的分析可知，在小跨度的范围内，求解的结果合理，但是实腹梁更加节约混凝土用量；在大跨度时，挠度相同的情况下，空腹梁不仅节约层高，而且节约混凝土用量；无论是大跨度还是小跨度，挠度相同的情况下，空腹梁均可以节约层高；

3）综合分析可知，等挠度法有理有据，具有一定的合理性、科学性，对工程实际应用有一定的科学应用价值。