基于数据驱动的潜射导弹出筒速度模型辨识*

罗珩娟 刘丙杰 张 庆

1.海军潜艇学院战略导弹与水中兵器系，青岛 266199； 2.中国人民解放军92330部队，青岛 266000

0 引言

潜射导弹因其机动范围广、攻击突然性强，装弹数量多、反击威力大等特点备受各大军事强国重视。潜射导弹弹射出筒经过水介质出水至空中再进入预定弹道，水下飞行段和出水段是潜射导弹发射所独有的过程，对发射结果影响巨大。出筒速度是影响导弹水下弹道姿态和发射精度的关键因素之一[1]，受众多客观条件影响，包括发射深度、海流速度、海浪高度、航速和气幕弹等，其中发射深度是最重要的影响因素。因此，控制潜艇在适合深度发射导弹，对提高导弹发射的成功率、确保军事任务完成率具有重要意义。目前，关于潜射导弹水中段飞行过程影响因素的研究主要包括海浪[2]、横向流[3]和气泡[4]等：文献[2]通过构建随机海浪模型进行统计仿真，得出了波浪对导弹弹道随深度变化的规律。文献[3]建立了导弹水下垂直发射横向动力学模型，对出筒过程中的横向振动进行了仿真，提出了减小横向流对导弹影响的有效方法。文献[4]研究了发射筒口气幕环境对导弹出筒过程中的受力影响并进行了仿真计算，结果证明气幕对出筒过程力学环境改变明显，影响导弹水中姿态。

本文通过相关分析，找到了影响潜射导弹出筒速度的最关键因素，即发射深度。在实测发射试验数据的基础上，使用三次样条差值方法，扩充样本数量并利用RBF神经网络、遗传神经网络和支持向量回归机分别对出筒速度模型进行训练,分别预测不同发射深度条件下潜射导弹出筒速度，对确保导弹安全可靠的发射意义重大。

1 出筒速度影响因素相关分析

相关分析[5]是研究事物之间是否关联且关联程度的统计方法。两个变量X,Y，如果X会随着Y的变化而变化，则认为两个变量相关，相关程度一般通过相关系数r表示。

(1)

相关系数r数值含义如表1所示。

表1 相关系数r含义表

利用SPSS分析软件分别求的各影响因素与出筒速度的相关系数、显著性如表2所示。

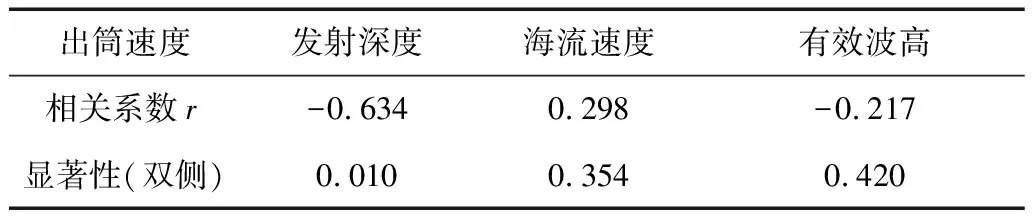
表2 各影响因素相关分析结果

可以看出出筒速度与发射深度相关性系数r=-0.634，显著性为0.01，即出筒速度与发射深度负相关，相关性较强，与海浪、波高、横向海流等其他因素相比，对出筒速度影响更大。

2 基于数据驱动的模型辨识方法

2.1 RBF神经网络

RBF神经网络[6]，称为径向基函数神经网络，是一种单隐层的前馈神经网络，其中隐层为径向基层。RBF神经网络用径向函数作为隐含层的“基”，输入层变量可以直接映射到隐含层空间。径向函数的中心点确定，映射关系对应产生，不再进行加权运算，所以收敛速度提高且不容易陷入局部最优，在工程领域应用广泛。RBF网络训练时，不断调整径向函数中心、方差以及隐层到输出层的权重值得到最优解。径向函数的选择对网络训练结果影响不大，最常用的是高斯函数，表达式为：

(2)

式中X=(x1,x2,x3,…,xn)为n维输入向量；cj为第j个基函数的中心；σj为第j个神经元的标准化常数，即高斯基函数的方差；n和p分别为输入层和隐含层的神经元的个数。网络输入和输出之间的关系表达式为：

(3)

式中m为输出层神经元的个数；yi为输出层第i个神经元的输出值；wj，i为隐含层第j个单元与输出层第i个单元之间的连接权值。

2.2 遗传神经网络

遗传算法(Genetic Algorithm，GA)[7]是对自然进化优胜劣汰，适者生存过程的模拟，通过选择、交叉、变异的三种运算方法进行问题求解。遗传算法有很好的全局优化能力，可以将其与BP神经网络[7]相结合寻求问题最优解。

遗传算法优化BP神经网络[8]主要可以分为3个环节，即：BP神经网络的建立，GA优化权重和阈值，BP神经网络的训练与预测，其基本流程如图1所示。

具体步骤为：

1)创建神经网络

根据待解决问题需要建立神经网络，确定网络隐含层层数，节点数和初始权重值和阈值。研究表明单隐层BP神经网络就可以解决绝大多数预测问题，故创建单隐层BP神经网络。

2)种群初始化与编码

对输入层到隐含层权重、隐含层阈值、隐含层到输出层权重、输出层阈值进行编码，并随机选择初始种群。

3)构造适应度函数

为了使BP网络预测更加准确，构造预测值与真实值误差函数倒数为适应度函数。

图1 遗传神经网络建立流程

4)遗传算法优化权重和阈值

遗传算子包括选择算子、交叉算子和变异算子3种，概率为ps，pc和pm，选择算子采用随机选择，交叉算子采用单点交叉方法，变异算子按pm概率产生变异基因数，如原基因编码为1，则变异为0，原基因编码为0，则变异为1。

5)网络训练和测试

将优化后的权重和阈值代入BP神经网络，计算预测误差是否满足用户需求，如满足网络训练结束，如不满足返回步骤3。

2.3 支持向量回归机

支持向量机(Support Vector Machines，SVM)是由Vapnik教授在1995年提出的，主要解决有限样本的学习问题，是目前泛化能力最强的技术之一，也是最适合小样本学习的技术之一。在SVM基础上引入不敏感损失函数ε，从而得到支持向量回归机(Support Vector Regression，SVR)[9]，基本原理是寻找一个最优面使所有训练样本离该最优面误差最小。通过发射试验结果基本可以看出出筒速度与发射深度是非线性关系，SVR将非线性关系的输入向量映射到一个高维度空间，在高维空间做线性回归分析，然后用一个核函数来代替高维空间中的内积运算，减轻了运算的复杂程度。

假设我们用一个线性函数f(x)=ω·x+b表示(xi,yi),i=1,2,…,n的回归方程，其中xi为输入向量，yi为输出向量，因此我们只需要求的ω和b即可确定回归方程。

支持向量回归机是基于统计学习理论的基于结构风险最小化原理，ε不敏感损失函数的定义是：

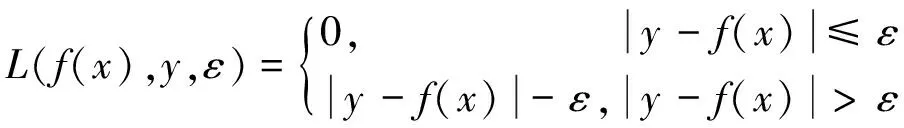
(4)

式中f(x)为回归函数的预测值，y为真实值，即真实值与预测值之差小于等于ε时，则损失为0。引入ξ和ξ*为非负的松弛变量，目标函数表示为

(5)

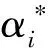
(6)

K(xi·x)是核函数，常见的有多项式核函数、高斯核函数、径向基数核函数和Sigmoid核函数等。

3 仿真分析

某型潜射导弹共进行了25次发射试验，试验数据如表3所示,散点图如图2所示。

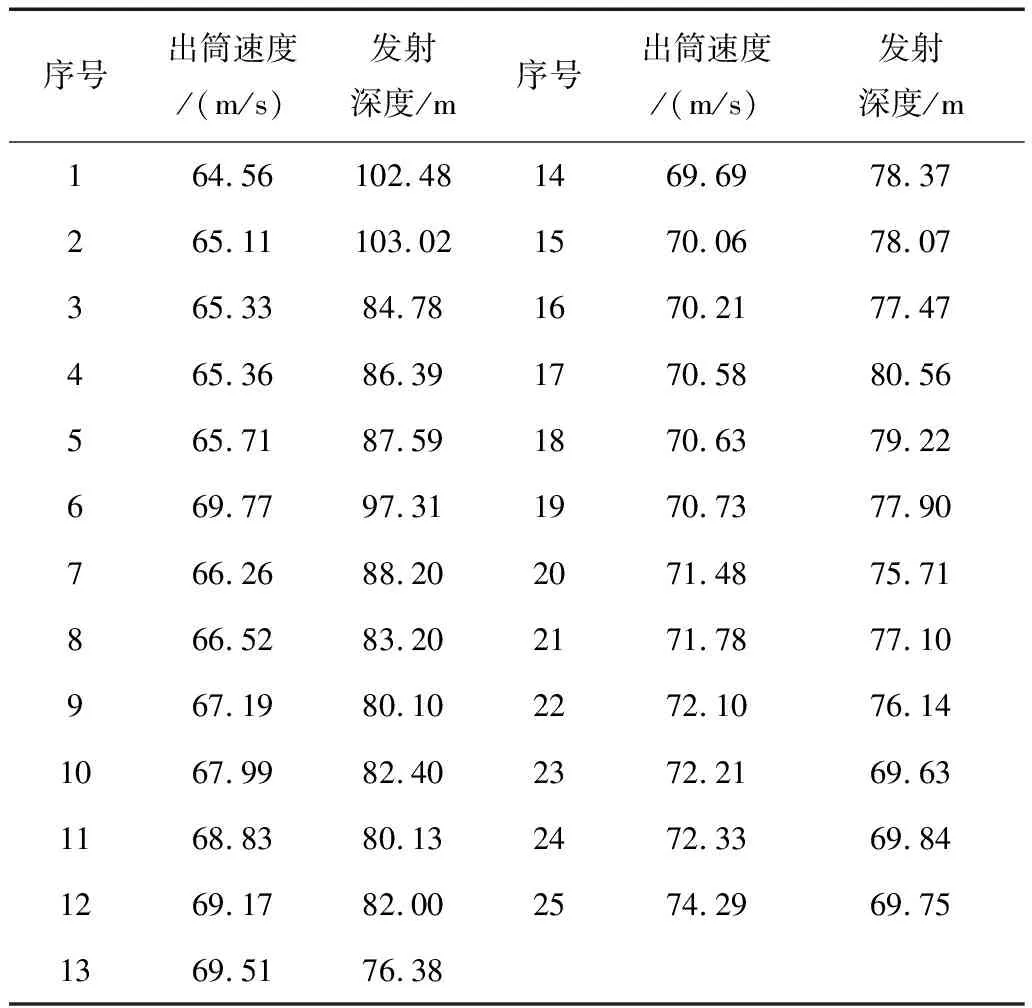
表3 导弹发射试验数据

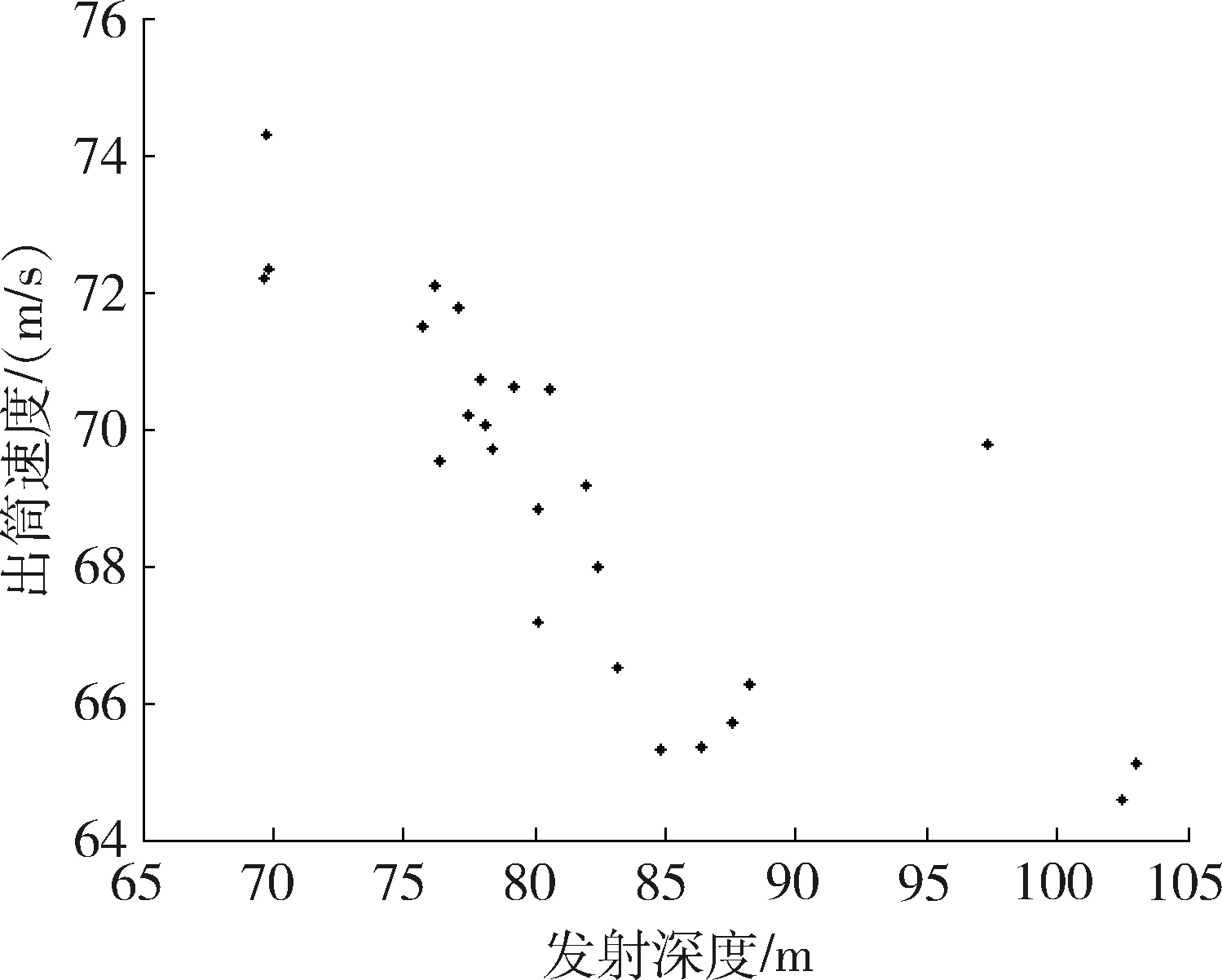
图2 发射试验结果散点图

潜射导弹试验次数有限，为提高模型训练准确度，引入cubic spline插值法，增加样本数量后训练模型。

3.1 cubic spline插值

样条插值最早应用于工业设计中，目的是为得到光滑的曲线，三次样条插值法(Cubic Spline Interpolation)[10]是其中应用较为广泛的一种。在数学上，三次样条插值主要用于函数拟合，使用三次多项式的拟合效果更好，更加符合实际要求。

经过三次样条插值处理，将原试验25组数据基础上扩展至1000组数据并绘制曲线，水下发射试验出筒速度与发射深度的对应关系如图3所示：

图3 插值处理后发射试验数据曲线图

3.2 仿真过程

三种模型训练均使用Matlab R2013b软件运行，取扩展后的前500组数据进行训练后，对全样本进行预测，运行环境如下：操作系统：Window7，Intel(R)Core(TM)i5-4300M，主频2.60GHz，内存2.99GB。

3.2.1 RBF网络训练

根据导弹发射试验数据，调用newrb函数建立RBF神经网络[11]，训练函数为Levenberg-Marquardt函数，训练方法为正交最小二乘法，收敛速度相对较快。网络经过训练后预测结果如图4所示。

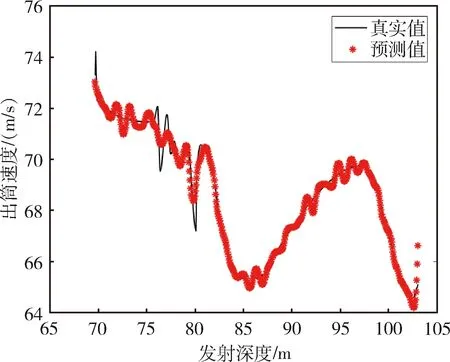
图4 RBF神经网络预测结果

3.2.2 遗传神经网络训练

利用遗传神经网络预测出筒速度，调用newff函数，创建单隐层BP神经网络，隐层神经元个数为32个，训练目标为0.001，最大迭代次数16000次，遗传算法运行参数设定如表4所示，优化前后连接权重与阈值对比如表5所示。

表4 遗传算法运行参数

表5 优化前后网络权重和阈值

使用随机权重和阈值的BP神经网络进行导弹出筒速度预测，经过4297次训练迭代后，模型均方误差缩小到9.968×10-4，误差估值与原值间拟合效果如图5和图6所示。

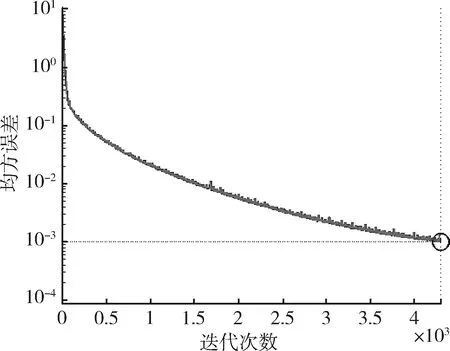
图5 BP神经网络训练效果

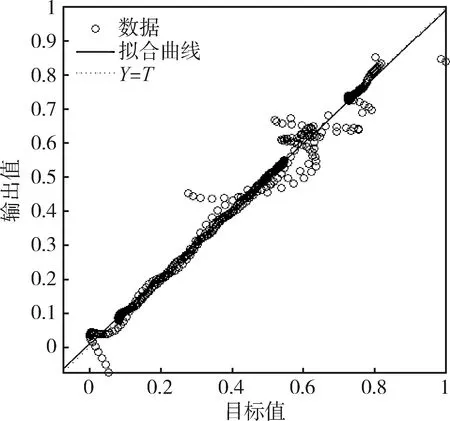
图6 BP神经网络拟合效果

使用遗传算法优化权重和阈值的BP神经网络进行导弹出筒速度预测，经过 3221次训练迭代后，模型均方误差缩小到 9.872×10-4，误差估值与原值间拟合效果如图7和图8所示。

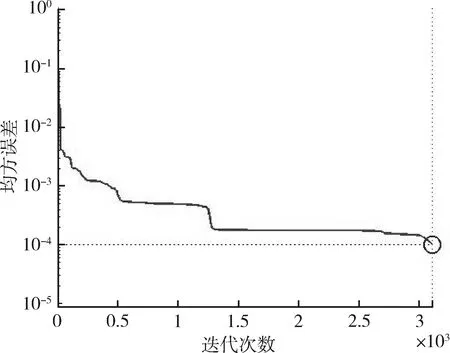
图7 遗传神经网络训练效果

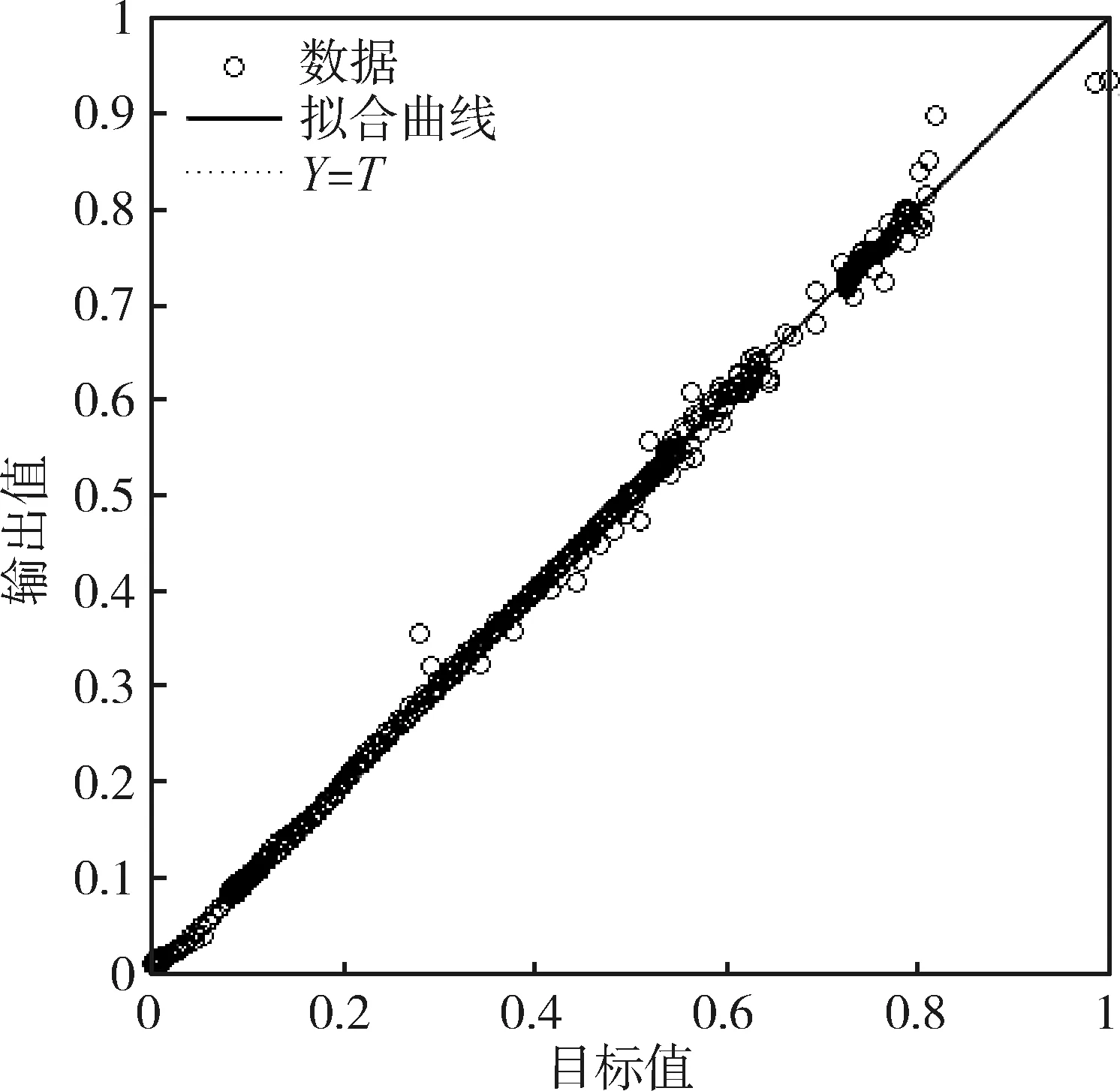
图8 遗传神经网络拟合效果

优化后预测结果如图所示：

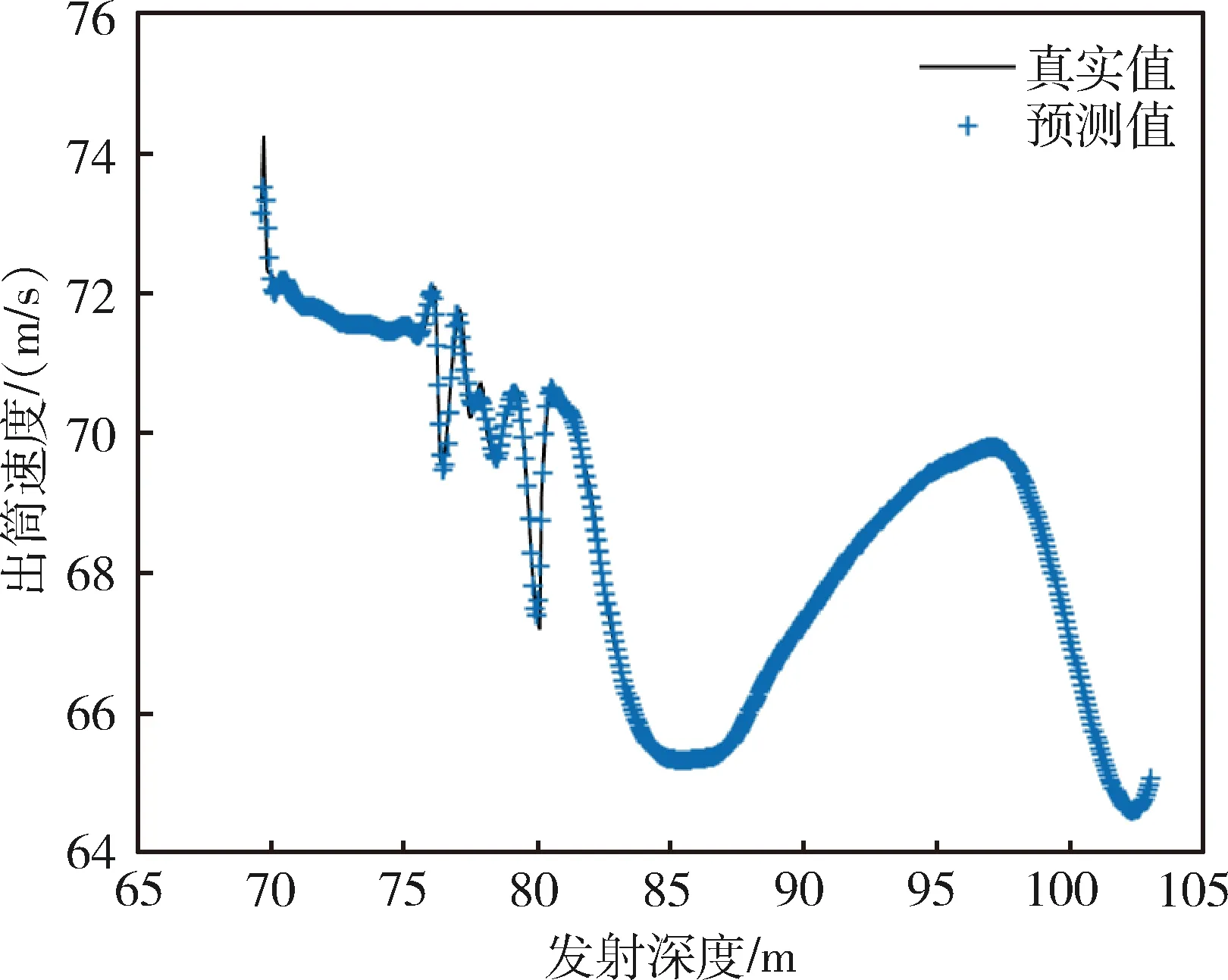
图9 遗传神经网络预测结果

3.2.3 支持向量回归机训练

利用SVR预测出筒速度，调用svmreg函数，设定惩罚因子C为1111，ε为0.01。已证明RBF核函数对应的模型泛化能力最好，选用高斯函数做核函数，预测结果如图10所示。

图10 支持向量回归机预测结果

3.3 仿真结果

综合对比3种模型，训练时间与预测精度稍有差异，对比结果如表6所示：

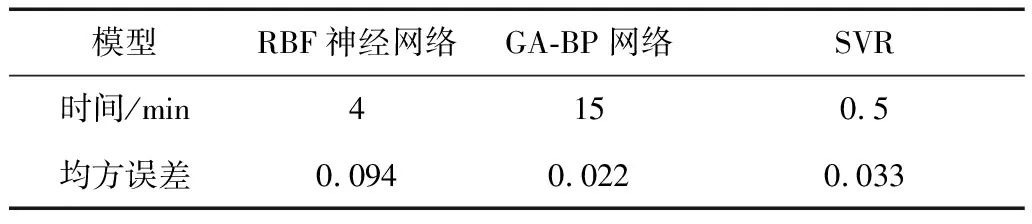
表6 模型预测结果对比

根据表6可以看出基于GA-BP网络模型的训练时间最长但预测精确度最高，基于SVR模型的训练时间最短，预测精度也较高，充分证明了SVR适合小样本学习的优势。导弹发射对可靠性要求极高，因此模型预测精确最为重要，建议选用GA-BP或SVR模型进行导弹出筒速度预测。

4 结束语

针对潜射导弹出筒速度影响因素的问题，根据基于实测潜射导弹发射试验数据，分析对比了导弹出筒速度与发射深度、海流速度和有效波高之间的相关程度并利用RBF神经网络、遗传神经网络和支持向量回归机建立模型，预测特定发射深度下的导弹水下发射出筒速度。结果表明：发射深度与导弹出筒速度呈负相关，是最显著的影响因素。基于支持向量回归机的模型训练时间最短，基于遗传神经网络的模型预测精确度最高。为进一步提高预测精度，未来将使用深度置信网络、广义回归网络等深度学习[12]方法建模预测，为探索潜射导弹的大深度发射提供依据。