高超声速飞行器的模糊分数阶PID控制*

张迎雪 管 萍 戈新生

北京信息科技大学 自动化学院，北京 100192

0 引 言

高超声速飞行器在国防事务和民用方面具有较高的战略价值[1]。2010年美国“猎鹰”计划下的HTV-2飞行器因未能有效应对气动参数的剧烈摄动，导致飞行失败[2]。因此构建一个能有效处理气动参数变化导致的不确定性的高精度姿态控制系统是目前亟待解决的问题之一。然而，面对复杂的飞行环境，传统PID控制具有一定的局限性。近年来，采用非线性和智能化的方法改进传统PID算法，获得了更高的精度和更强的鲁棒性[3]。文献[4]中俯仰通道控制器的设计融合了模糊与模型参考自适应方法，通过实时调节PID参数使系统具有自适应能力。文献[5]设计了PID控制和自抗扰控制互为补充的无扰切换控制，解决了两种模式之间的过渡问题。然而，上述文献仅考虑了单一俯仰通道的设计。文献[6]设计的模糊控制器带有修正因子，在姿态控制仿真实验中，取得了较好的控制效果。然而并未考虑气动参数大范围变化给系统带来的影响。将分数阶微积分与PID控制相结合构成分数阶PID控制，不仅调节范围更广，而且能够为系统提供更加灵活、准确的控制[7]。

本文为实现高超声速飞行器在气动参数剧烈变化时快速精准跟踪姿态角期望值，构建了模糊分数阶PID控制器。分数阶PID的计算由于增加了2个可调参数，调节范围得到进一步扩展，计算中有对过去项的累加，使系统具有记忆特性，能提升控制精度及稳定性。为更好处理气动特性快速变化带来的不确定性，加入模糊的方法对控制器参数进行在线调节，以提高系统的动态性能和自适应性。由仿真结果可以看出，所提出的控制策略能够更好地实现飞行器姿态角的精准跟踪，并验证了对气动参数摄动的鲁棒性。

1 高超声速飞行器模型

根据高超声速飞行器的飞行特点，得到飞行器姿态控制的仿射非线性数学模型[8]，如式(1)～(2)：

(1)

(2)

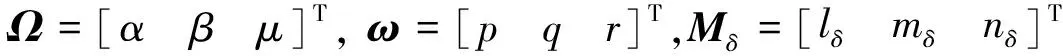
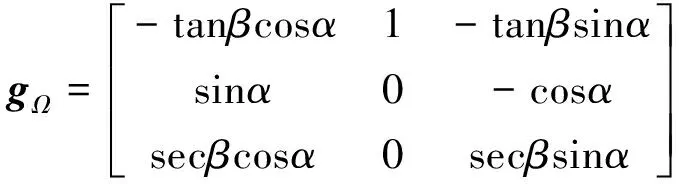
式中参数具体释义详见文献[9]。在运动过程中，因气动参数变化导致模型中含有不确定项。令fΩ=fΩ0+DΩ，fΩ0是fΩ的标称值，DΩ是因fΩ中CL,α,CY,β变化产生的不确定部分。令Mδ=Mc+ΔMδ，Mc=[lcmcnc]T是由气动舵面偏转δ=[δeδaδr]T产生的控制力矩，ΔMδ是Mδ中因气动参数变化产生的不确定项。令fω=fω0+Δfω，fω0是fω的标称值，Δfω是fω中因laero,maero和naero中气动参数变化产生的不确定部分。令Dω=gωΔMδ+Δfω。通过引入气动参数变化导致的不确定项，可将式(1)和(2)转换为：

(3)

(4)

本文的控制目标是，设计合适的控制力矩Mc，让高超声速飞行器可以快速精确跟踪姿态角期望值，并且能对气动参数出现的大幅变化进行有效抑制，具备强鲁棒特性。

2 基于模糊分数阶PID控制器设计

2.1 分数阶的计算

(5)

由上述分析可得在此定义下μ的分数阶积分：

(6)

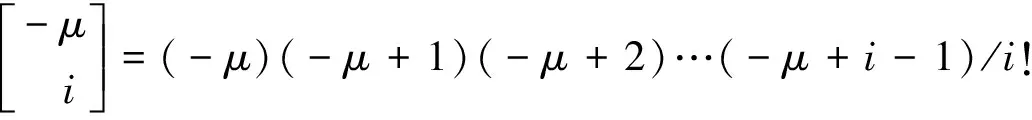
在上式中有对u(t-ih)项的累加，过去时刻的函数值对此时分数阶微积分均有一定程度的影响。利用信息记忆能力，系统可以取得更优的控制性能。

2.2 分数阶次λ，μ的选取对控制系统性能的影响

分数阶PID控制器的一般形式为：

U=kp·e(t)+ki·D-λe(t)+kd·Dμe(t)

(7)

kp,ki和kd为控制器中比例、积分、微分项系数，μ和λ表示微分、积分阶次。Dμ和D-λ分别表示对系统误差e(t)的μ阶导数和λ阶积分。U为控制器的输出。

在传统PID控制中，积分项可以起到减小稳态误差的作用，实现对期望值的精确跟踪。控制器中引入分数阶次λ后，当λ较小时，控制系统可以取得较快的响应速度，上升时间和调节时间缩减，超调小，然而可能存在一定的静态误差。随着λ的增大，积分作用逐渐增强，伴随超调量、上升时间和调节时间的增加，系统的稳定性明显变弱。当λ过大时，系统会出现严重的振荡[11]。

传统PID控制中，选取合适的微分项可以减少系统的超调量和动态误差，增强稳定性。引入分数阶次μ后，随着μ的减小，控制系统的稳态误差逐渐减少，动态响应精度明显提高，会增大超调和响应时间。若μ过小，控制系统将很难稳定。当分数阶次μ逐渐增大，系统的超调量和调节时间会相应减少[11]。λ和μ的引入，增加了系统结构的灵活性，控制精度得到改善，鲁棒性更强。

2.3 模糊分数阶PID控制器设计

高超声速飞行器需要克服气动参数摄动带来的不确定影响。加入模糊的方法对控制器参数进行在线调节，可有效处理系统的不确定部分，增强鲁棒性。为此本文针对高超声速飞行器的姿态控制系统构建了模糊分数阶PID控制器。

基于奇异摄动理论将整个控制系统分为快速、慢速闭环回路，并分别设计模糊分数阶PID控制器。快回路是控制角速度的内环，慢回路是控制姿态角的外环，飞行器控制系统结构图如图1所示。

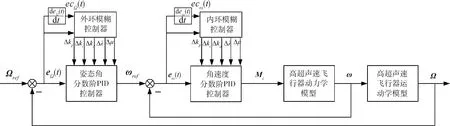
图1 高超声速飞行器控制系统结构图

将姿态角期望值Ωref与实际值Ω之间的误差eΩ(t)作为姿态角分数阶PID控制器的输入，将eΩ(t)和ecΩ(t)作为外环模糊控制器的输入，由外环模糊控制器推算得到姿态角分数阶PID控制参数的修正量ΔkpΩ,ΔkiΩ,ΔkdΩ,ΔλΩ,ΔμΩ。用修正后得到的分数阶PID参数计算出角速度期望值ωref。将ωref与实际角速度ω之间的差值eω(t)作为角速度分数阶PID控制器的输入。利用eω(t)及ecω(t)作为内环模糊控制器输入，在线修正kpω,kiω,kdω,λω和μω5个参数，并用修正后的参数计算控制力矩Mc，用于飞行器姿态控制系统。

2.3.1 外环回路控制器的设计

系统姿态角的期望值Ωref=[αrefβrefμref]T与姿态角实际值Ω=[αβμ]T之间的误差为：

eΩ(t)=Ωref-Ω

(8)

将eΩ(t)作为姿态角分数阶PID控制器的输入，通过式(15)计算得到角速度参考值ωref：

ωref=kpΩ·eΩ(t)+kiΩ·D-λΩeΩ(t)+
kdΩ·DμΩeΩ(t)

(9)

kiΩ，kpΩ和kdΩ代表姿态角控制器中的PID参数，μΩ和λΩ分别是微分和积分阶数，ωref=[prefqrefrref]T。

为了增强系统的鲁棒性，引入模糊控制对kpΩ,kiΩ,kdΩ,λΩ和μΩ进行实时调节。限于篇幅，在此仅详细介绍外环模糊控制器中俯仰通道的设计，滚转及偏航通道的设计与此相类似。外环模糊控制器在俯仰通道上的输入为eΩ1(t),ecΩ1(t)，输出为ΔkpΩ1(t),ΔkiΩ1(t),ΔkdΩ1(t),ΔλΩ1(t)和ΔμΩ1(t)。

根据攻角误差eΩ1(t)及其变化率ecΩ1(t)确定实际变化范围[-eΩ1max,eΩ1max]，[-ecΩ1max,ecΩ1max]，将其均变换到离散论域[-0.6,0.6]上[8]。

选取外环模糊控制器输出变量ΔλΩ1(t),ΔμΩ1(t)的离散论域为[-0.6,0.6]，分别乘以比例因子KΔλΩ1和KΔμΩ1后，得到ΔλΩ1(t),ΔμΩ1(t)的实际值[-ΔλΩ1max,ΔλΩ1max],[-ΔμΩ1max,ΔμΩ1max]。

对eΩ1(t),ecΩ1(t)和ΔλΩ1(t),ΔμΩ1(t)选取模糊集合均为NB，NS，NM，ZO，PS，PM，PB；其隶属度函数均选为高斯型函数。参照上述λ和μ的调节方法，设计了分数阶ΔλΩ1，ΔμΩ1的模糊控制规则表，如表1～2所示。

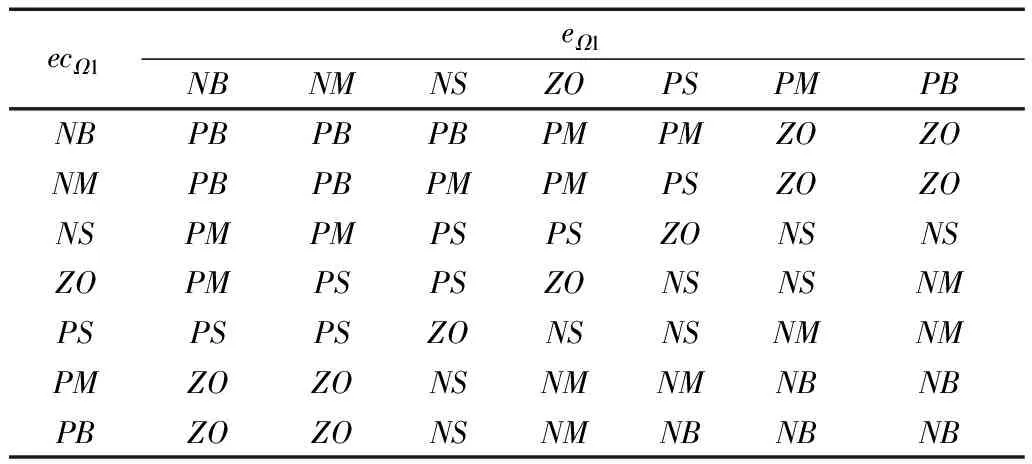
表1 ΔλΩ1的模糊规则表

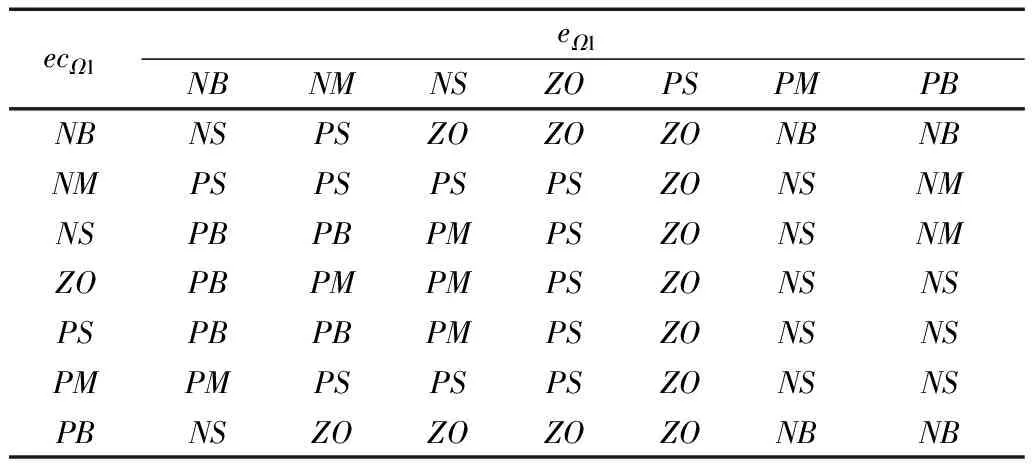
表2 ΔμΩ1的模糊规则表

外环模糊控制器采用Mamdani型，根据表1～2进行模糊推理，并采用重心法进行反模糊化。图2～3分别为ΔλΩ1和ΔμΩ1的模糊推理规则表面图。

图2 ΔλΩ1的模糊推理规则表面图

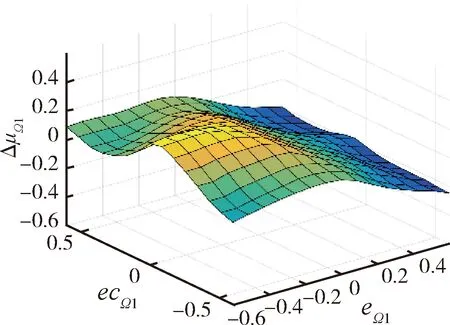
图3 ΔμΩ1的模糊推理规则表面图

由外环模糊控制器得到精确修正量，对λΩ1,μΩ1实时调整如下：

(10)

对于外环模糊控制器其它输出变量ΔkpΩ1(t),ΔkiΩ1(t)和ΔkdΩ1(t)，选取离散论域为[-6,6]的范围。将其乘以比例因子KΔ kpΩ1,KΔ kiΩ1,KΔ kdΩ1，得到输出变量的实际值。

外环模糊控制器的输出ΔkpΩ1(t),ΔkiΩ1(t),ΔkdΩ1(t)与ΔλΩ1,ΔμΩ1的模糊集合选取一致，其隶属度函数均为高斯型。ΔkpΩ1,ΔkiΩ1,ΔkdΩ1的模糊规则表可参考文献[11]。模糊PID控制器使用Mamdani型推理，用重心法解模糊。经外环模糊控制器调节后的PID系数更新如下：

(11)

通过式(10)和式(11)对5个系数进行在线调整，利用更新后的kpΩ1,kiΩ1,kdΩ1,λΩ1和μΩ1作用于控制器(式(9))，得到角速度的期望值ωref。

2.3.2 内环回路控制器的设计

姿态角分数阶PID控制器的输出=ωref与实际角速度ω之间的误差为eω(t)：

eω(t)=ωref-ω

(12)

将eω(t)作为角速度分数阶PID控制器的输入，通过式(13)计算得到控制力矩Mc：

Mc=kpω·eω(t) +kiω·D-λωeω(t) +kdω·
Dμωeω(t)

(13)

kpω,kiω和kdω为PID系数,λω,μω为分数项阶次。

将姿态角误差eω(t)及其导数ecω(t)共同作用于内环模糊控制器。限于篇幅仅介绍内环模糊控制器中俯仰通道的设计，偏航与滚转通道的设计与此相似。俯仰通道中5个模糊控制器的输入均为eω1(t),ecω1(t)，输出分别为Δkpω1(t),Δkiω1(t),Δkdω1(t),Δλω1(t)和Δμω1(t)。

与外环模糊控制器设计相似，将内环模糊控制器输入变量eω1(t),ecω1(t)的实际变化范围变换到离散论域[-0.3,0.3]上。分别选取输出变量Δλω1(t),Δμω1(t)和Δkpω1(t),Δkiω1(t),Δkdω1(t)的离散论域为[-0.3,0.3]和[-3,3]的范围。

eω1(t),ecω1(t),Δλω1(t),Δμω1(t)Δkpω1(t),Δkiω1(t),Δkdω1(t)选取模糊集合PB,NB,PM,NM,PS,NS,ZO，隶属度函数为高斯型。Δλω1,Δμω1,Δkpω1,Δkiω1,Δkdω15个参数的模糊规则表与外环模糊控制器相似，限于篇幅不再列出。内环模糊控制器仍采用Mamdani型，依照规则表进行模糊推理，用重心法去模糊化最终输出精确值的修正量。根据内环模糊控制器求出的精确修正值对5个参数进行如下实时调节。

(14)

用在线修正后得到的参数值计算姿态角速度分数阶PID控制(式(13))。通过在线调节控制器参数以解决气动参数扰动带来的不确定问题。

3 仿真研究

对高超声速飞行器采用模糊分数阶PID控制并进行仿真验证。仿真验证中高超声速飞行器采用式(1)～(2)所示的非线性模型形式，其中参数M=82310kg,Ma=8.8,b=223.79m,c=12.07m。高超声速飞行器的惯性矩阵为[8]：

初始姿态角和初始角速率分别为Ω0=[2° 1° 3°]T,ω0=[0 0 0]T，姿态角的期望值为Ωref=[5° 0° 6°]T。

经反复调试，内环控制器参数较优的初值可取kpω= [50 12 80]T,kiω= [0.1 0.01 0.1]T,kdω= [0.1 0.1 0.1]T,λω=0.6,μω=0.6。外环可将kpΩ= [20 60 40]T，kiΩ= [0.8 0.1 0.1]T,kdΩ= [0.1 0.1 0.1]T,λΩ=0.6,μΩ=0.6作为控制器参数的初值。

对高超声速飞行器分别采用所提的模糊分数阶PID控制与传统PID控制进行仿真。标称气动参数下，可得到如图4～6的响应曲线。

标称气动参数下姿态角动态响应的性能指标如表3。由仿真结果可以看出，在传统PID控制中姿态角到达稳态的响应时间较长，且具有较大的超调；而在所提的模糊分数阶PID控制下，3个姿态角到达稳态的时间更短。本文所提的控制策略通过对历史项的累加，使控制系统具有记忆特性，加快了系统的响应速度。对比姿态角速度和控制力矩响应曲线，模糊分数阶PID控制策略不仅超调量小，而且能够迅速实现精准跟踪。

为了验证所提控制策略对气动参数变化的鲁棒性，对飞行器气动参数摄动做了仿真研究，图7～8是不同情况姿态角响应曲线。

姿态角的调节时间如表3所示。与传统PID控制相比，模糊分数阶PID控制器增加了2个可调参数，扩大了调节范围。引入模糊方法能够实现控制器参数的在线调节。故当气动参数剧烈变化时，传统PID控制下姿态角响应出现了较大的波动，超调大且响应时间长，而本文采用的控制策略姿态角响应快，超调量小，自适应性强。仿真结果显示模糊分数阶PID控制对气动参数变化的抑制能力更强，体现了更好的鲁棒性。

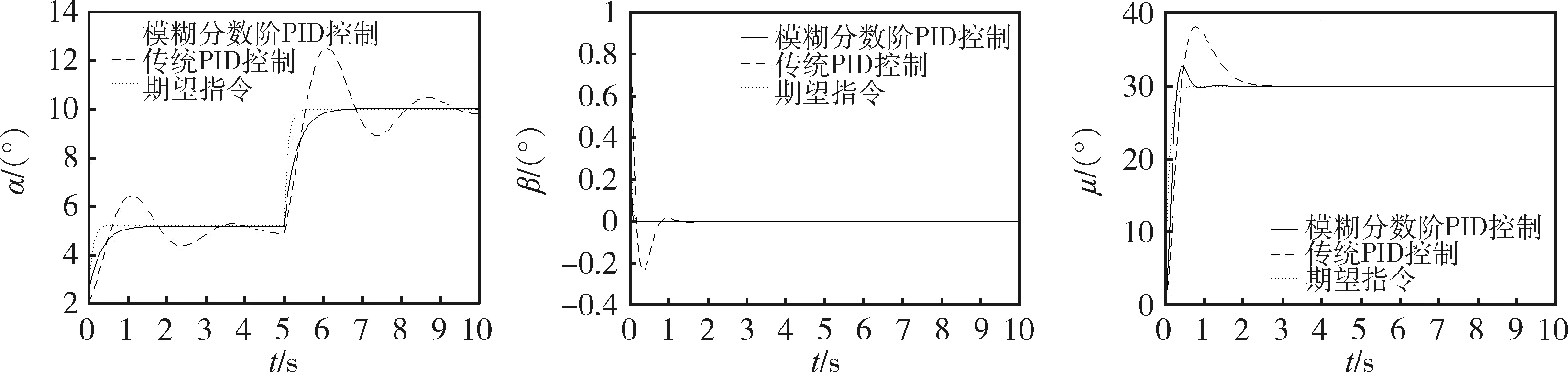
图4 标称情况下姿态角α,β.μ 对比曲线

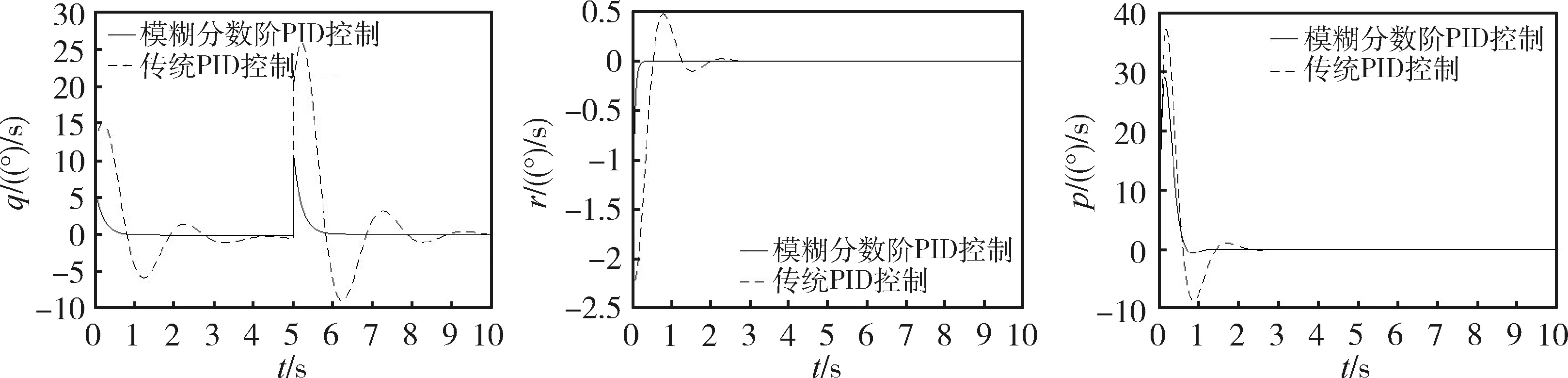
图5 标称情况下姿态角速度q,r,p对比曲线

图6 标称情况下控制力矩mc,nc,lc 对比曲线

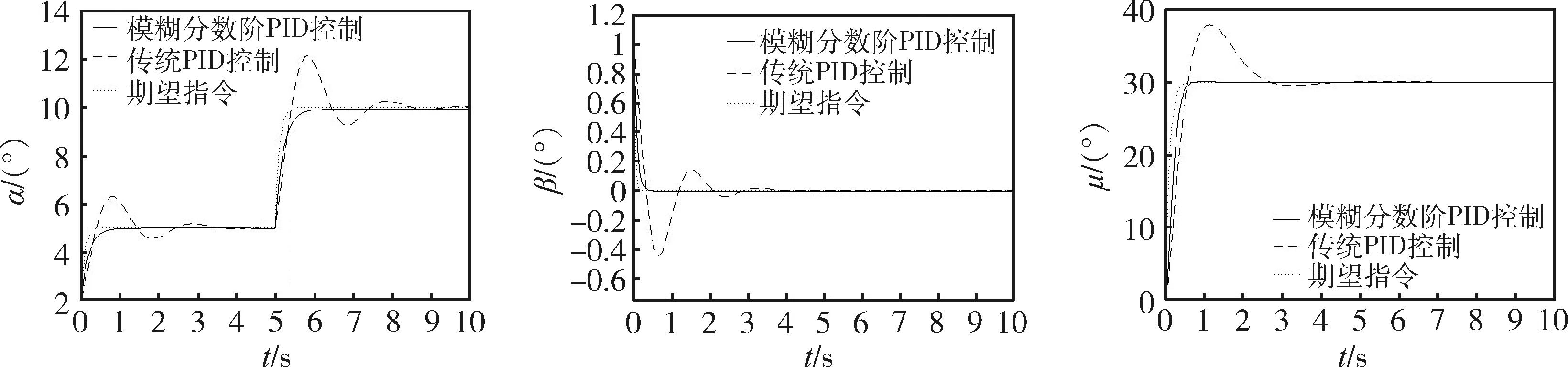
图7 气动参数增加50%时α,β,μ跟踪对比曲线

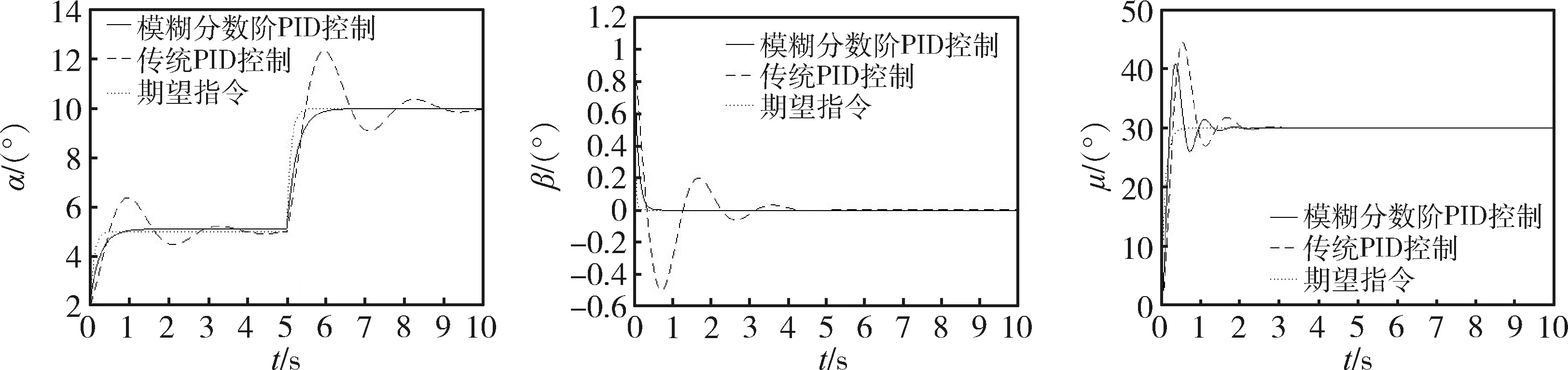
图8 气动参数减少50%时α,β,μ跟踪对比曲线

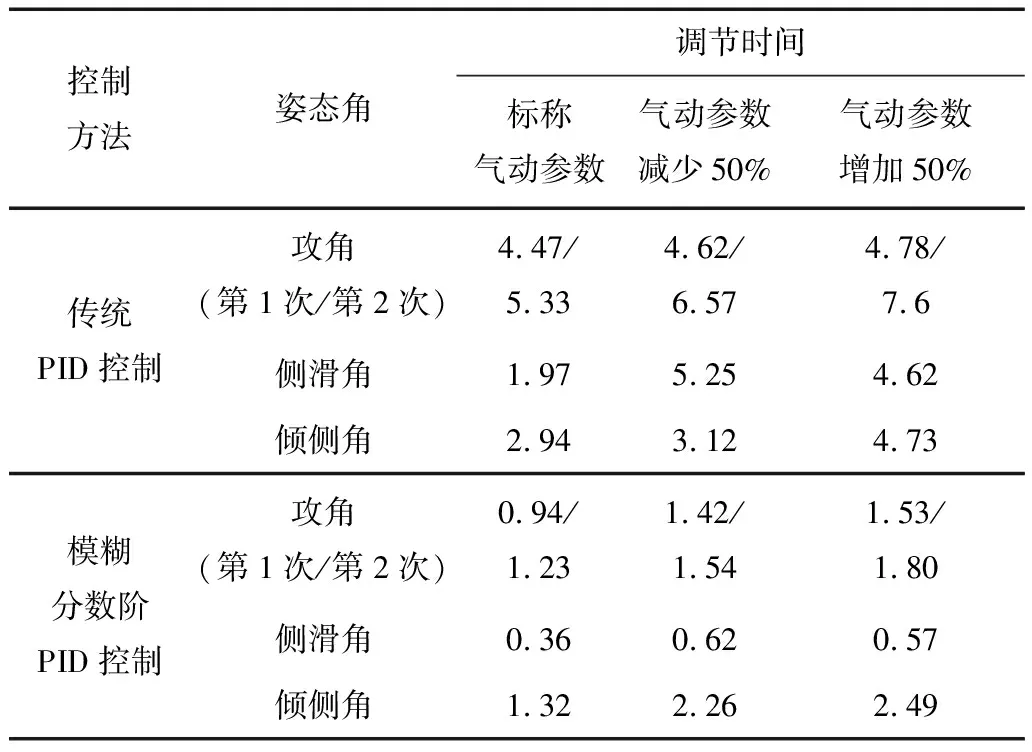
表3 不同控制策略性能指标对比

4 结 论

考虑高超声速飞行器气动参数摄动，提出模糊分数阶PID控制策略。控制器中因加入分数阶运算，系统具有更广阔的调节空间，且分数阶的计算具有信息记忆特性等优势，从而加快了系统响应，增强了稳定性。采用模糊的方法对系统参数在线调整，增强了系统对气动参数变化的鲁棒性。兼具分数阶PID和模糊控制两者优势的模糊分数阶PID控制策略，不仅能够实现飞行器姿态角快速精准跟踪，还有效抑制了气动参数的剧烈变化。仿真结果显示本控制策略有更好的动态性能、鲁棒性强，且算法简单，易于工程实现，具有广阔的应用前景。