基于水平集的医学图像分割算法

房巾莉，吕毅斌，王樱子，唐胜男，武德安

(1.昆明理工大学 理学院,云南 昆明 650500;2.昆明理工大学 计算中心,云南 昆明 650500;3.电子科技大学 数学科学学院,四川 成都 611731)

目前，图像分割[1-2]广泛应用于工程学、计算机科学、统计学、物理、化学、医学、遥感等领域。在医学中，通过对图像感兴趣区域的定位和分割，可以得到更多更准确的医疗数据，有助于开展后续诊断治疗研究等。

经过多年的研究，国内外研究者提出大量的图像分割方法，并将其应用到医学图像处理领域。随着人工智能的发展，基于深度神经网络的医学影像分割方法[3]被提出，并在很多图像处理领域取得了较好的结果，成为目前主流的图像分割方法。然而，在处理超精细图像中，基于图像信息的传统分割算法能得到更有效的结果。目前，研究者们提出了很多结合机器学习和传统分割模型的方法[4-6]。尽管人工智能、大数据等现代技术在医疗分割领域的应用已成大势所趋，但传统分割模型依然扮演着重要角色。

在传统模型中，活动轮廓模型(Active Contour Model，ACM)是一种具有良好性能的分割算法。Caselles等人[7-8]于1993年和1995年将水平集理论[9]和ACM结合提出几何活动轮廓模型，即水平集方法。该方法在分割过程中将轮廓曲线作为零水平集隐式地包含在水平集函数中，从而很自然地处理曲线的拓扑结构变化。水平集方法中，由Chan和Vese在2001年提出的Chan-Vese (C-V)模型[10]最具有代表性。该模型对噪声有一定的鲁棒性，但仍然存在缺点，例如水平集对初始轮廓敏感，重新初始化数值步骤较复杂，无法分割一些灰度不均的图像等。为了提高C-V 模型分割的准确性，研究者们提出了许多改进方法。Li等人提出了局部二值拟合模型[11](Local Binary Fitting，LBF)，利用高斯窗口函数，构造局部拟合能量，较好地解决灰度不均的图像分割问题。之后，Li等人[12]又深入研究了核函数的选择依据和局域区域范围大小的选择及其作用，提出RSF(Region-Scalable Fitting)模型。Wang等人[13]将局部能量与C-V模型叠加，提出局部CV(Local CV，LCV)模型。Caselles等人[14]利用梯度信息构造驱动力项，有利于分割边缘梯度大的目标。Lankton等人[15]提出基于区域的模型，将C-V模型的均值分段计算，因此可以应用于灰度不均的图像。Shi等人[16]通过用分段常数函数近似水平集函数，简化迭代规则，提出了一个快速算法。Li等人[17]提出距离正则水平集演化(Distance Regularized Level Set Evolution，DRLSE)，并将其成功应用于一个基于边界的主动轮廓模型。张等人[18]将C-V水平集模型的区域项变形归一化为强度指示算子后，替代了DRLSE模型驱动项中的强度指示算子，将区域和边缘信息嵌套结合提出RESLS(Region and Edge Synergetic Level Set Framework)模型。

本文提出了一种快速的结合全局和局部信息的水平集模型，命名为HLSGL模型(Hybrid Level Set Model Based on Global and Local Term)。本研究基于C-V分割算法，从两方面进行改进：(1)针对待分割图像的灰度不均匀现象，在能量泛函构造的过程中，引入局部统计信息能量项；(2)为避免演化曲线陷入局部最优且防止过度分割，引入速度停止函数，使得水平集函数更光滑，分割更快。

1 水平集分割算法

1.1 基本原理

参数化主动轮廓模型中，定义一条封闭且连续的参数化轮廓曲线C(s,t)=(x(s,t),y(s,t))。其中，t为时间，s是任意参数化变量，s∈[0,1]，并设曲线单位内向法向矢量为N。C(s,t)在能量方程的作用下，沿着法线方向演化，逼近图像边界。曲线的演化方程为

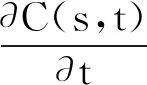
(1)

其中，F是轮廓曲线演化的速度函数，曲线上各点的运动方向为单位法向矢量方向。

用式(1)描述曲线演化的方法有其局限性：计算曲线的固有参数，如曲率、单位法向矢量等比较困难。难以应付闭合曲线在演化过程中发生拓扑变化的情况。而水平集方法为轮廓曲线C(t)提供一种隐式表达方式，将C(t)作为零水平集嵌入到水平集函数φ中，即

C(t)={(x,y)|φ(x,y,t)=0}

(2)

对上式两边分别关于时间求偏导数得

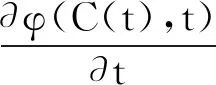
=0

(3)

(4)

将式(1)、式(4)代入式(3)，可得水平集函数的演化方程

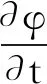
(5)

其中，F为水平集函数演化的速度函数。不同问题可以有不同的速度函数形式。

1.2 水平集函数的重新初始化

为保证数值精度，要求水平集函数具有一定的光滑性，并且在演化过程中必须保持为符号距离函数。李纯明[19]提出在水平集函数演化过程中引入一个能量惩罚项，约束水平集函数使其保持为近似的符号距离函数。该能量惩罚项可表示为

(6)

2 C-V模型

设I是原图像，x代表像素点，Ω代表图像域。其能量泛函定义如下

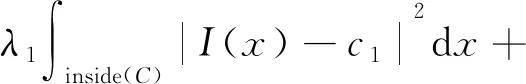
μ·Length(C)

(7)

其中，C是演化的轮廓曲线；c1和c2分别表示曲线C内部和外部的平均灰度值；λ1，λ2和μ是正常数。式(7)的前两项构成驱动力项；第3项是长度约束项，用来平滑水平集轮廓。当曲线C到达边界时，能量泛函才能取得最小值，曲线位置就是目标的轮廓所在。

引入水平集函数φ(x)来代替演化曲线C，选取两个正则化的函数Hε(z)和δε(z)表示演化曲线的内部和外部

(8)

(9)

于是C-V模型的能量泛函改写为

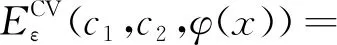
(10)

固定φ(x)，上式分别对c1、c2求导，可以得到c1、c2的更新计算式

(11)

(12)

固定c1、c2，由梯度下降流可得水平集函数演化的Euler-Lagrange方程

(13)

由于C-V模型基于区域能量，对噪声有一定的鲁棒性，可适用于没有明显边缘的目标。但忽略图像局部区域信息容易导致对一些灰度不均的图像分割失败。

3 HLSGL模型

传统的C-V水平集方法使用全局信息来构造能量方程，对于灰度不均的医学图像，会产生分割误差。为了更好地处理这一类图像的分割问题，需要改进构造能量泛函。本文将全局和局部信息融合在一起，提出一种新的水平集能量泛函，使分割不受灰度不均匀效应的影响。特别地，通过在模型中引入速度停止函数，可得到较高精度的分割结果。

3.1 局部信息

引入局部统计信息对于解决灰度不均匀问题非常必要，首先需要对图像灰度不均匀问题进行描述。图像中出现灰度不均匀现象有两方面原因，一是硬件干扰因素，如不均匀光照；二是成像物体本身因素，如物体的形状和位置。而医学图像存在局部体积效应，以及人体组织器官相互重叠和其成像过程带来的噪声等，灰度不均匀现象更加常见。研究者对图像灰度不均匀效应建立了很多数学模型，其中文献[20]假设灰度不均匀效应是在原始图像域里加入了一个空间变化的光滑函数场，数学模型描述为

I″=BI′+m

(14)

其中，I″是含灰度不均匀效应的图像；B是灰度不均匀场；I′是灰度均匀图像；m为噪声。但是产生灰度不均匀效应的因素比较多且过于复杂，因此对灰度不均匀效应进行建模是不现实的。虽然学者们已经提出了很多灰度不均匀校正算法[21-23]，但消除灰度不均匀效应至今仍然是一个难以解决的问题。因此，直接研究在灰度不均匀图像中进行曲线演化以逼近真实边缘尤为重要。式(14)中，一般情况下B在局部区域是缓慢变化的，甚至在小区域中是定值，因此在C-V水平集模型中融入局部统计信息，能量泛函定义为

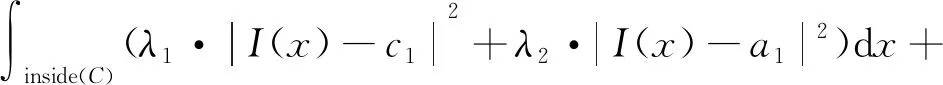
μ·Length(φ(x))+P(φ(x))

(15)

其中，前两项是驱动力项，P(φ(x))代表式(6)的避免重新初始化的能量惩罚项；a1、a2分别表示平均卷积算子后的图像在轮廓曲线内外像素的局部灰度均值

(16)

(17)

其中，“*”代表卷积符号；KA表示均值核。将局部项与全局项结合，一方面对核窗口大小的选择不过于敏感；另一方面可对灰度不均图像得到良好的演化效果。

引入局部统计信息后，之所以能成功地分割灰度不均匀图像，是因为将图像每个像素在其邻域内的局部统计特性a1、a2结合全局灰度平均值c1和c2后，可以更准确地计算出内部能量和外部能量，进一步表达为轮廓曲线上的膨胀力和收缩力，从而促使轮廓曲线逼近真正边缘。而利用C-V模型对灰度不均匀的图像进行分割时，只有原图的像素值与全局算术平均值之差来表示轮廓曲线内外受力，使得没有达到真正目标边界时轮廓就可能因受到膨胀力和收缩力相互制约，而停止在非目标边界的位置。如图1所示，分割一幅灰度不均的图像，图1(c)是用C-V模型分割的结果，分割失败。本文增加局部统计信息后，对图像边缘具有较好的局域化效果，避免了分割中膨胀力和收缩力在非边界处就相互制约的现象，成功分割了灰度不均的图像，如图1(d)所示。

(a) (b) (c) (d)图1 灰度不均图像，图像大小为75×79(a)原始图像 (b)初始轮廓曲线 (c)利用C-V模型的分割结果 (d)利用式(15)的分割结果Figure 1. Segmentation of an inhomogeneous image with size of 75×79(a)Original image (b) Initial contour (c) Segmentation result of C-V model (d) Segmentation result by equation (15)

3.2 速度停止函数

在活动轮廓模型中，速度停止函数一般为式(18)所示，由外函数g和内函数|Gσ*I(x)|构成。其目的是在去除噪声的同时保留图像边缘信息，调节轮廓曲线演化速度，并使轮廓曲线在目标边缘演化停止

(18)

其中，Gσ代表均值为0且方差为σ的高斯核；“*”代表卷积算子；代表梯度算子。

图2 两种速度停止函数g(x)和h(x)的曲线Figure 2. Curves of two speed stopping functions g(x)、h(x).

速度停止函数g(x)满足：(1)对于任意|Gσ*I(x)|的值，都有g(x)>0；(2)g(x)是一个单调递减函数，并且针对以上特征，本文采用一种新的速度停止函数h(x)，定义为

(19)

如图2，新的速度停止函数h(x)与式(18)的g(x)对比，横坐标x代表|Gσ*I(x)|，函数初值均为1，但曲率不同，g(x)的曲线较陡峭，h(x)的曲线下降较缓慢。利用这一区别，可以在不同类型图像中选取不同的速度停止函数：当目标与背景梯度差别小时，边缘梯度和其他部分差距不明显，选用较陡峭的停止函数，分割效果较好；当目标与背景梯度差别大时，边缘梯度大，选用下降较缓慢的停止函数，避免分割伪边界。

根据以上分析，在式(15)的驱动力项中引入速度停止函数，从而提出HLSGL模型，能量泛函定义为

EHLSGL=

μ·Length(φ(x))+P(φ(x))

(20)

为了验证速度停止函数在水平集方程中的作用，用两幅图像来测试HLSGL模型，如图3所示。图3中的第1行为合成噪声葫芦图像，第2行为蛋白细胞图像。从图3看出，第3列的分割效果比第2列更光滑准确。表1列出了每个实验的迭代次数和时间，可以看出引入速度函数后减少了实验迭代次数和分割时间。

(a) (b) (c)图3 无h(x)和有h(x)的HLSGL模型的分割结果对比(a)初始轮廓曲线 (b)无h(x)的式(15)的分割结果 (c)有h(x)的式(20)的分割结果Figure 3. Comparison of segmentation results between the model of equation (15) and HLSGL model of equation (20) (a) Initial contours (b) Segmentation results by equation (15) (c) Segmentation results by equation (20)

表1 图3的迭代次数和分割时间的对比

图3测试了HLSGL模型引入速度停止函数h(x)的优势，而引入不同类型的速度停止函数对分割效果的影响也不同。现在将HLSGL模型中的速度停止函数分别选取式(18)和式(19)的g(x)、h(x)，在两幅图像中进行对比，结果如图4所示。图4中第1行是灰度不均匀的合成图像，第2行是大米图像。实验参数为：μ=0.01；第1行的第2图取λ1=0.1，λ2=7；第3图取λ1=0.1，λ2=10；第2行的第2和第3图均取λ1=λ2=1。从图4可以看出，当HLSGL模型选取传统速度函数g(x)时，分割失败，未达到边界导致分割精度低；当HLSGL模型选取速度函数h(x)时，分割结果较好。表2为图4中实验结果的分割效率对比，可以看出选取h(x)时，可以减少迭代次数，提高分割效率。

(a) (b) (c)图4 选取不同速度停止函数的HLSGL模型的分割结果对比(a)初始轮廓曲线 (b)选取传统速度函数g(x)时HLSGL模型的分割结果 (c)选取速度停止函数h(x)时HLSGL模型的分割结果Figure 4. Comparison of the segmentation results of HLSGL models with different speed stopping functions(a) The initial contours (b) Segmentation results by HLSGL using g(x) (c) Segmentation results by HLSGL using h(x)

表2 图4的分割效率对比

4 数值实现

在引入水平集后，将总能量方程式(20)的能量泛函改写为

EHLSGL=

(21)

在演化过程中只有曲线C到达目标边界时，其能量泛函最小。应用梯度下降法求解式(21)的最小值，可得水平集演化的Euler-Lagrange方程

[-λ1(I(x)-c1)2-λ2(I(x)-a1)2+

λ1(I(x)-c2)2+λ2(I(x)-a2)2]+

(22)

HLSGL模型的迭代终止条件为：迭代次数n达到设置的最大迭代次数Numiter，或者在规定的连续迭代次数Num内，均满足

(23)

可以针对不同图像来设置Numiter、Num和ω的值。

HLSGL模型的分割算法的输入为待分割图像，输出为图像轮廓曲线，初始轮廓曲线步骤如下：

步骤1设置能量项参数λ1、λ2、μ；设置均值核窗口和高斯核窗口σ均为15；设置最大迭代次数Numiter，取Num=15，ω=5；

步骤2选定初始轮廓曲线位置，构造相应的初始水平集函数φ0(x)；

步骤3利用式(22)计算φn+1(x)=φn(x)+Δt(∂φn(x)/∂t)，得到更新的水平集函数φn+1(x)。其中，n是迭代次数；Δt是步长，取Δt=0.1；

步骤4检验演化是否满足迭代终止条件。若满足，则停止演化，输出分割图像，水平集函数φn+1(x)的零水平集曲线为最终轮廓；否则返回步骤3。

5 实验结果与分析

通过实验验证HLSGL模型的分割能力，包括分割精确性，鲁棒性和计算效率。实验环境为Lenovo-PCIntel(R)Core(TM)i3-4000MCPU2，40GHz、4GB内存的计算机和Windows10操作系统。在MATLABR2016a开发平台下运行实验程序。该部分所有实验的速度停止函数均选用h(x)。

5.1 对初始轮廓的鲁棒性

首先，在不同的初始轮廓下，对一幅噪声图像进行分割，HLSGL模型的参数均为λ1=λ2=1，μ=0.03，Numiter=20。如图5所示，无论初始轮廓在分割目标的内部、外部或与目标区域相交，HLSGL模型均能进行较好的分割，验证了HLSGL模型对初始轮廓的鲁棒性。

(a) (b) (c) (d)图5 不同初始轮廓下HLSGL模型的分割结果(a)轮廓曲线在所有目标外部 (b)轮廓曲线与目标相交 (c)轮廓曲线在一个目标外部 (d)轮廓曲线在一个目标内部Figure 5. Segmentation results of HLSGL with different initial contours(a) Outside the two targets (b) Cross the targets (c) Outside a target (d) Inside a target

5.2 应用于灰度不均医学图像

为了验证HLSGL模型对灰度不均匀效应的处理能力，将其应用于灰度不均的医学图像，如图6所示。图中前3行为灰度不均血管图像，第4行是手指CT图像。由实验结果看出，所提方法可以得到清晰完整的目标边界，也表明HLSGL模型对灰度不均匀效应的鲁棒性。表3列出了这组实验的参数和迭代次数和运行时间。

(a) (b) (c) (d)图6 HLSGL模型对灰度不均医学图像的分割结果(a)原始图像 (b)初始轮廓 (c)分割结果 (d)分割结果的二值图像Figure 6. Segmentation results of HLSGL for inhomogeneous images(a) Original images (b) Initial contours (c) Segmentation results (d) Binary images of segmentation result

表3 图6中实验的参数和分割迭代次数和运行时间

5.3 应用于含弱边界的医学图像

进一步对含弱边界的医学图像进行实验，来检测HLSGL模型的能力。如图7所示，前两行分别是肾囊肿图像、肝囊肿图像，第3行是脑肿瘤图像。可以看到这些图像带有噪声、灰度不均、弱边界等分割困难。由分割结果看出HLSGL模型对这些图像进行分割均得到了较精确的结果，表明除了对噪声和灰度不均现象的鲁棒性外，HLSGL模型对弱边界有较强的提取能力。表4列出了这组实验的参数、迭代次数和运行时间。

(a) (b) (c) (d)图7 HLSGL模型对含弱边界的医学图像的分割结果(a)原始图像 (b)初始轮廓 (c)分割结果 (d)分割结果的二值图像Figure 7.Segmentation results of HLSGL for medical images with weak boundaries(a) Original images (b) Initial contours(c) Segmentation results (d) Binary images of segmentation result

表4 图7的参数、迭代次数和运行时间

5.4 对比试验

为进一步验证HLSGL模型的分割能力，本文进行了两类对比实验，第一类是与典型的结合局部信息的主动轮廓模型(LBF模型、RSF模型、LCV模型)进行对比；第二类是与有代表性的水平集模型(Casellesetal.模型、C-V模型、Lanktonetal.模型、Shietal.模型)进行对比。为了定量评价HLSGL模型，本研究将分割结果同专家手工分割结果进行定量比较，采用基于面积的Dice相似性系数[24-25](DiceSimilarityCoefficient，DSC)指标进行比较。DSC的定义如下

(24)

其中，RA和RB为专家分割区域和实验分割结果区域。DSC值越接近于1，表明分割精度越高。

5.4.1 与典型的结合局部信息的水平集模型对比

首先，由于HLSGL模型是基于C-V模型而引入图像局部信息，LBF模型、RSF模型、LCV模型均是结合局部信息的水平集模型。因此，将HLSGL模型与C-V模型、LBF模型、RSF模型、LCV模型进行对比。如图8所示，保证初始轮廓一致，分别对灰度不均的子宫囊肿图像、灰度不均的腕关节图像、灰度不均的骨裂图像进行分割。HLSGL模型的实验参数为：对于子宫囊肿λ1=1，λ2=3，μ=0.01；对于腕关节λ1=1，λ2=5，μ=0.01；对于骨裂图λ1=0.1，λ2=1，μ=0.01。由图8得出，灰度不均现象使C-V模型、LBF模型、RSF模型、LCV模型的分割结果容易陷入局部最小值。相反地，由于HLSGL模型对灰度不均效应的鲁棒性，HLSGL模型可以得到较准确的目标边界，同时对凹边界和弱边界均有较强的提取能力。表5列出了图8各模型分割结果的DSC值、迭代次数和运行时间。为方便比较DSC值，如图9折线图看出，HLSGL模型的DSC值均高于0.9，对每幅图得到相对高的分割精度。经对比，HLSGL模型的计算效率较高，但是对于骨裂图来说迭代次数稍多。

(a) (b) (c) (d) (e) (f)图8 不同模型的分割对比图(a)初始轮廓 (b) C-V模型 (c)LBF模型 (d)RSF模型 (e)LCV模型 (f)本文模型Figure 8. Comparison of different segmentation models (a) Initial contours (b) C-V model (c) LBF model (d) RSF model (e) LCV model (f) HLSGL model

表5 图8的DSC值、迭代次数和运行时间对比

图9 图8中各模型分割结果的DSC对比图Figure 9. DSC comparison plots of the segmentation results by each model in Figure 8

5.4.2 与有代表性的水平集模型对比

本文HLSGL模型与几个有代表性的水平集模型(包括Casellesetal.模型、C-V模型、Lanktonetal.模型、Shietal.模型)用相同的初始轮廓进行分割的效果对比。图10是一幅肺部CT图像，图11是一幅视网膜血管图像。HLSGL模型的参数为：对肺部CT为λ1=1，λ2=4.5，μ=0.01，对视网膜血管图像为λ1=λ2=1，μ=0.01。由图10和图11可看出：Casellesetal.模型和Lanktonetal.模型均分割失败；传统C-V模型对灰度不均匀图像的分割效果较差，演化曲线陷入局部极小值，没能达到理想的分割效果；Shietal.模型有部分细节过分割；而本文方法在分割中具有明显的优势，由图10和图11的第2行可以看出，其演化曲线更趋近于目标边界，轮廓更光滑。表6列出了图10和图11中各模型分割结果的DSC值、迭代次数和运行时间，可看出本文方法在分割精度和分割效率上明显优于其他模型，DSC值均高于0.9。

图10 各模型对肺部CT的分割结果对比(a)初始轮廓曲线 (b)Caselles et al.模型 (c)C-V模型 (d)Lankton et al.模型 (e)Shi et al.模型 (f)HLSGL模型 (g)HLSGL模型分割的最终轮廓 (h)HLSGL模型分割结果的目标提取Figure 10. Comparison of segmentation results of lung CT by different models(a) Initial contour (b) Caselles et al.model (c) C-V model(d)Lankton et al.model(e) Shi et al.model (f) HLSGL model(g) Final contour by HLSGL model(h) Target by HLSGL model

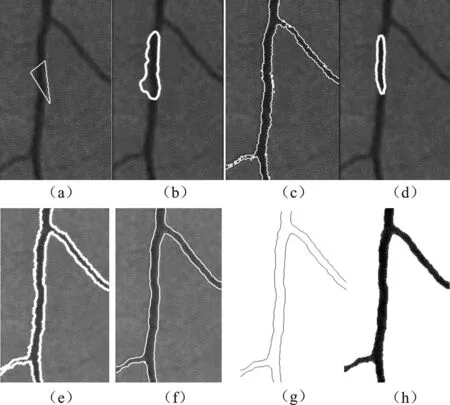
图11各模型对视网膜血管图像的分割结果对比(a)初始轮廓曲线 (b)Caselles et al.模型 (c)C-V模型 (d)Lankton et al.模型 (e)Shi et al.模型 (f)HLSGL模型 (g)HLSGL模型分割的最终轮廓 (h)HLSGL模型分割结果的目标提取Figure 11. Comparison of segmentation results of retinal blood vessel images by different models (a) Initial contour (b) Caselles et al. model(c) C-V model (d) Lankton et al. model (e) Shi et al. model(f) HLSGL model (g) Final contour by HLSGL model(h) Target by HLSGL model

表6 图10及图11的DSC值、迭代次数和运行时间对比

6 结束语

本文研究了医学图像分割问题，提出一种结合局部和全局统计信息的水平集分割算法，名为HLSGL。保留C-V算法全局信息的同时，在能量泛函中引入局部信息，使之与全局灰度均值叠加使算法对图像边缘具有全局和局域化效果，避免了轮廓曲线的膨胀力和收缩力在非边缘处制约导致的分割失败。在驱动力项中引入速度停止函数，在迭代过程调节水平集曲线演化速度，得到较光滑的边缘曲线，更加准确快速地分割图像。通过医学图像分割实验，验证了改进算法的准确性、鲁棒性和计算效率。本文算法对含有噪声、弱边缘以及灰度不均的医学图像有明显优势。今后的研究中，会研究速度停止函数的选择及作用，以及核函数的选择。