船舶垂荡运动下转子-隔振系统的非线性动力学分析

张文卓, 李 明

(西安科技大学力学系，西安 710054)

由于风浪的影响，船舶在航行时易于平衡位置附近发生周期性的纵摇、垂荡和横摇等牵连运动[1-2]，这些牵连运动会对船舶动力装置运行的稳定性造成影响。为保证船舶能够安全、稳定的航行，对船用转子-轴承系统减振方面的研究十分必要。而气囊-浮筏隔振装置因其构造紧凑，以及优异的低频振动抑制效果，已广泛应用于船用转子-轴承系统的振动控制问题[3]。

目前，关于牵连运动下转子-轴承系统振动特性的研究工作还处于发展阶段。文献[4]利用第二类Lagrange方程建立了飞行器作机动飞行时转子系统的一般模型，研究了机动飞行条件下发动机转子的动力学行为，且与试飞数据具有较好的一致性；而文献[5]基于Hamilton原理，讨论了机动飞行条件下直升机尾传动轴的振动方程，并研究了机动飞行条件下直升机尾斜轴横向弯曲的动力学行为；文献[6]则通过引入基础运动速度，推导出一种改进的滑动轴承油膜力模型，并研究了基础运动的振幅和频率变化对转子系统非线性动力学行为的影响。文献[7]基于短轴承理论，讨论了船舶垂荡运动下转子系统的稳态响应变化规律，结果表明垂荡运动改变了转子系统进入混沌的路径。

而在关于浮筏隔振装置的非线性动力学行为和振动控制的相关研究中，文献[8]考虑了浮筏和基础板的弹性变形，建立了浮筏动力学运动方程，并通过数值方法研究了浮筏隔振器的刚度变化对系统振动特性的影响；而文献[9]基于长轴承理论，推导了附加气囊支撑浮筏隔振装置的转子系统运动方程，并通过数值方法讨论了该系统的稳态响应变化规律；文献[10]则研究了具有双层QZS(quasi-zero-stiffness)构造的隔振浮筏系统，并对该系统的振动抑制性能进行了系统分析，结果显示，两自由度QZS装置在隔振方面更具优势，QZS装置对阻尼比敏感，质量比是低频隔振设计中的关键参数。文献[11]根据振动机械到浮筏弹性基础上的最小动力传递准则，通过代价函数研究了惯性致动器在浮筏上的最佳安装位置，从而对振动机械进行主动振动控制。

以上研究集中在分析牵连运动下转子-轴承系统的非线性振动规律，以及浮筏隔振系统的动力学特性和振动抑制问题。而目前关于牵连运动下转子-隔振系统振动特性和动力学控制方面的研究较少。现基于气囊的强非线性特征，讨论船舶垂荡运动条件下具有立方刚度和线性阻尼的气囊-浮筏隔振装置耦合转子-轴承系统的动力学分岔规律，并研究气囊-浮筏隔振装置对转子系统振动的抑制效果，以期为船用转子-隔振系统的非线性动力学设计和振动控制提供理论依据和分析方法。

1 数学模型

1.1 运动方程

图1为船体垂荡运动形式及具有气囊-浮筏隔振装置的转子-轴承系统示意图。为方便动力学模型的建立，设R0(x0,y0,z0)为固连于地面的惯性参考系，R1(x1,y1,z1)和R2(x2,y2,z2)为固连于船体分别用来描述转子和浮筏运动的非惯性参考系，而固连于圆盘的R(x,y,z)为局部坐标系。将船体在惯性参考系R0(x0,y0,z0)中沿x0轴平移的垂荡运动规律简化为xh=ahsin(Ω0t)，其中ah和Ω0分别为垂荡运动幅值和角频率。

图1 垂荡作用下具有气囊-浮筏隔振装置的转子-轴承系统示意图Fig.1 Schematic diagram of rotor-bearing system with additional the air bag-floating raft vibration isolator under heaving motion

将浮筏和轴承基座简化为一个质量单元，而气囊基于其强非线性特征简化为具有立方刚度和线性阻尼的弹簧，如图2所示。

图2 气囊-浮筏隔振装置示意图Fig.2 Schematic diagram of the air bag-floating raft vibration isolator

根据牛顿运动定律，可得船体垂荡运动条件下，具有气囊-浮筏隔振装置的船用转子-轴承系统运动方程为

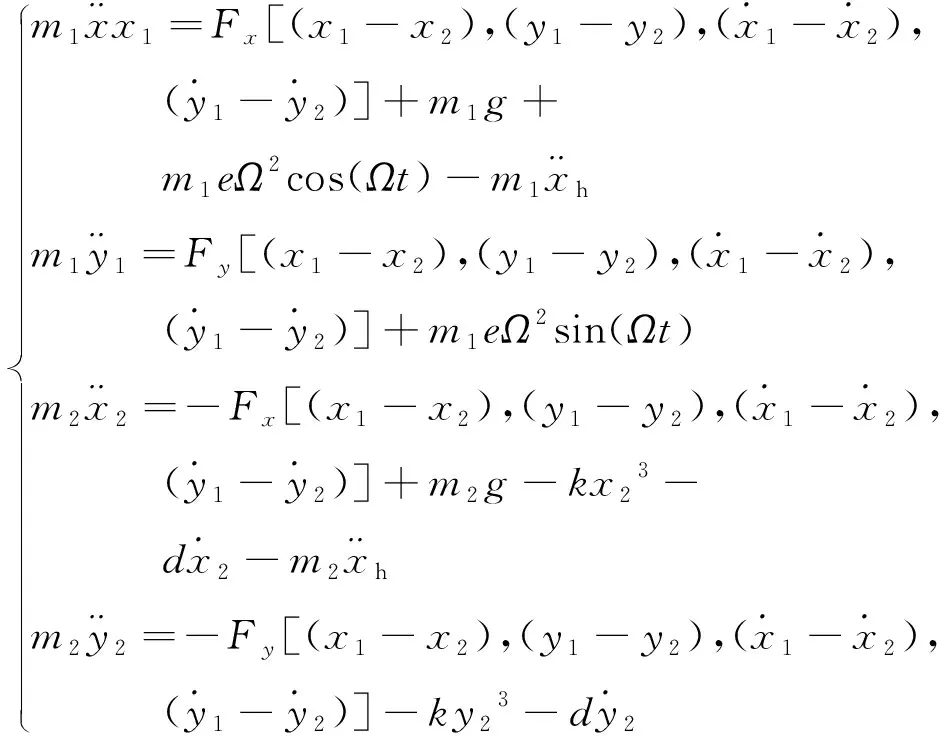
(1)

式(1)中：m1为转子质量；m2为浮筏及基座质量；e和Ω分别为转子偏心距和转子转速；Fx和Fy为作用于转子的轴承非线性油膜力[12-13]；k和d分别为气囊刚度及阻尼；g为重力加速度。

1.2 油膜力模型

滑动轴承结构如图3所示。轴颈和轴瓦被润滑油分开而不发生接触，油膜使轴颈具有承载能力，还能大幅度减少转子系统的表面磨损。

O为轴承几何中心，Om为转子质量中心图3 滑动轴承示意图Fig.3 Diagram of sliding bearing

基于长轴承理论，即轴承直径比其长度小得多，则油膜压力沿轴向的变化远比其沿周向的变化小[12]。根据这一假设，雷诺方程可表示为

庐山西海位于江西省西北部,地处九江和南昌之间,区位优势明显。庐山西海距九江和南昌较近大约都在100公里以内,而且南北都有机场，距离大约都在80公里以内,并且有多条交通线路经过（如京九铁路、昌九高速公路、105国道等线路）,区位优势十分明显。

(2)

式(2)中：p和R分别为油膜压力和轴承半径；φ、β分别为偏位角与周向方位角；e0、c和μ分别为轴承偏心距、油膜间隙和润滑油黏度；h为油膜厚度，h=c(1+εcosβ)，ε为偏心率，ε=e0/c。

基于Gümbel边界条件将油膜压力分布函数p沿轴承表面进行两次积分。可得非线性油膜力的径向分力Fr和周向分力Fτ的表达式[13]为

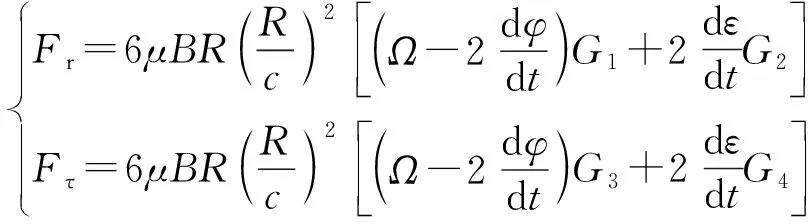
(3)

将油膜力通过坐标变换投影到x和y方向为

(4)

1.3 无量纲运动方程

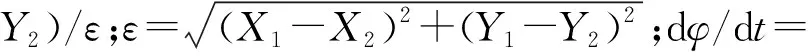
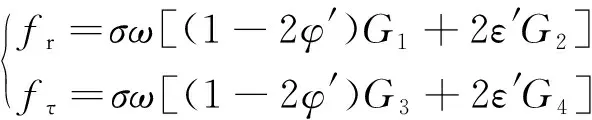
(5)

表1 无量纲参数表达式

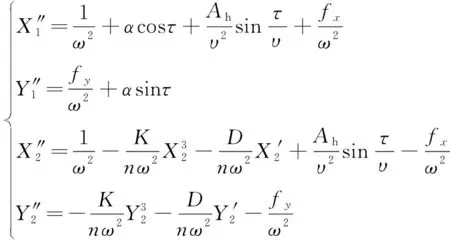
(6)

2 结果与讨论

式(6)是一个具有4自由度的强非线性微分方程组，对其进行解析研究较为困难，故利用4～5阶Runge-Kutta法求解，得到系统的稳态响应、分岔图和最大Lyapunov指数曲线等以分析隔振装置的减振性能以及转子系统的非线性动力学行为[14]。

2.1 隔振系统对转子振动的抑制

为凸显气囊-浮筏隔振装置对转子系统振动的抑制效果，给出图4所示的不考虑隔振装置时船舶垂荡运动下转子系统分岔图作为对比，取系统参数结合图4、图5可以分析气囊-浮筏隔振装置对转子振幅的抑制效果，其结果如表2所示。

为σ=3，Ah=120，υ=[30,70]。而图5为船舶垂荡运动下附加气囊-浮筏隔振装置的转子系统分岔图，此时为参数σ=3，υ=[30,70]，Ah=120，n=7.5，K=9，D=0.2。

图6为α=0.1时，船舶垂荡运动下不考虑隔振装置时转子系统动力学响应分岔图及对应的最大Lyapunov指数曲线。而图7为参数α=0.1时，附加气囊-浮筏隔振装置的转子系统在船舶垂荡运动下的稳态响应分岔图及最大Lyapunov指数(LLE)曲线。

对比图6、图7可得出气囊-浮筏隔振装置对转子系统动力学分岔特性的影响，将相关分析结果在表3中列出。

图4 垂荡运动下无隔振装置的转子系统分岔图Fig.4 Bifurcation diagram of rotor system without vibration isolator under heaving motion

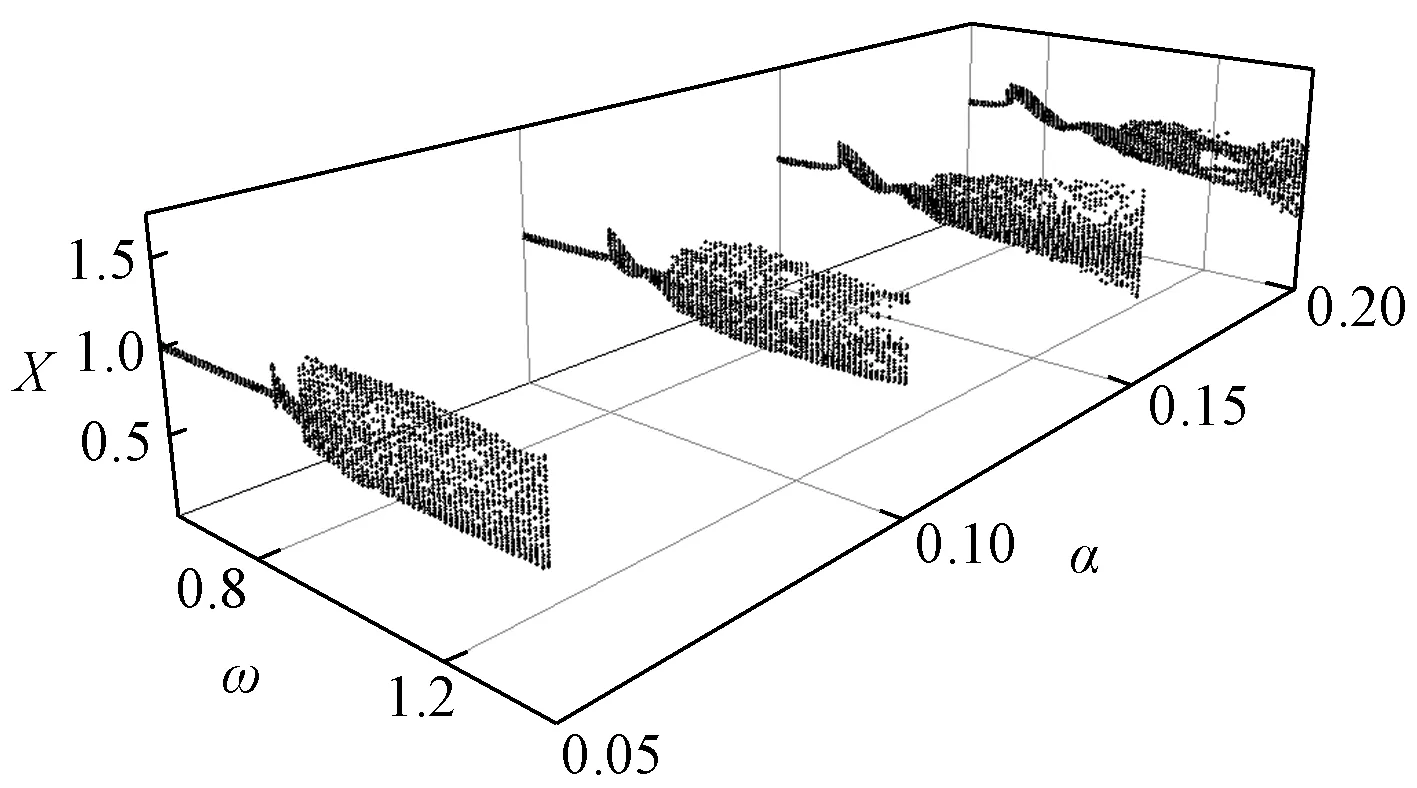
图5 垂荡运动下气囊-浮筏隔振装置耦合转子系统分岔图Fig.5 Bifurcation diagram of rotor system with air bag-floating raft vibration isolator under heaving motion

表2 隔振装置对转子振幅的抑制分析

图6 垂荡运动下无隔振装置的转子系统在α=0.1时的分岔图及最大Lyapunov指数Fig.6 Bifurcation diagram and largest Lyapunov exponents of rotor system without vibration isolator under heaving motion when α=0.1

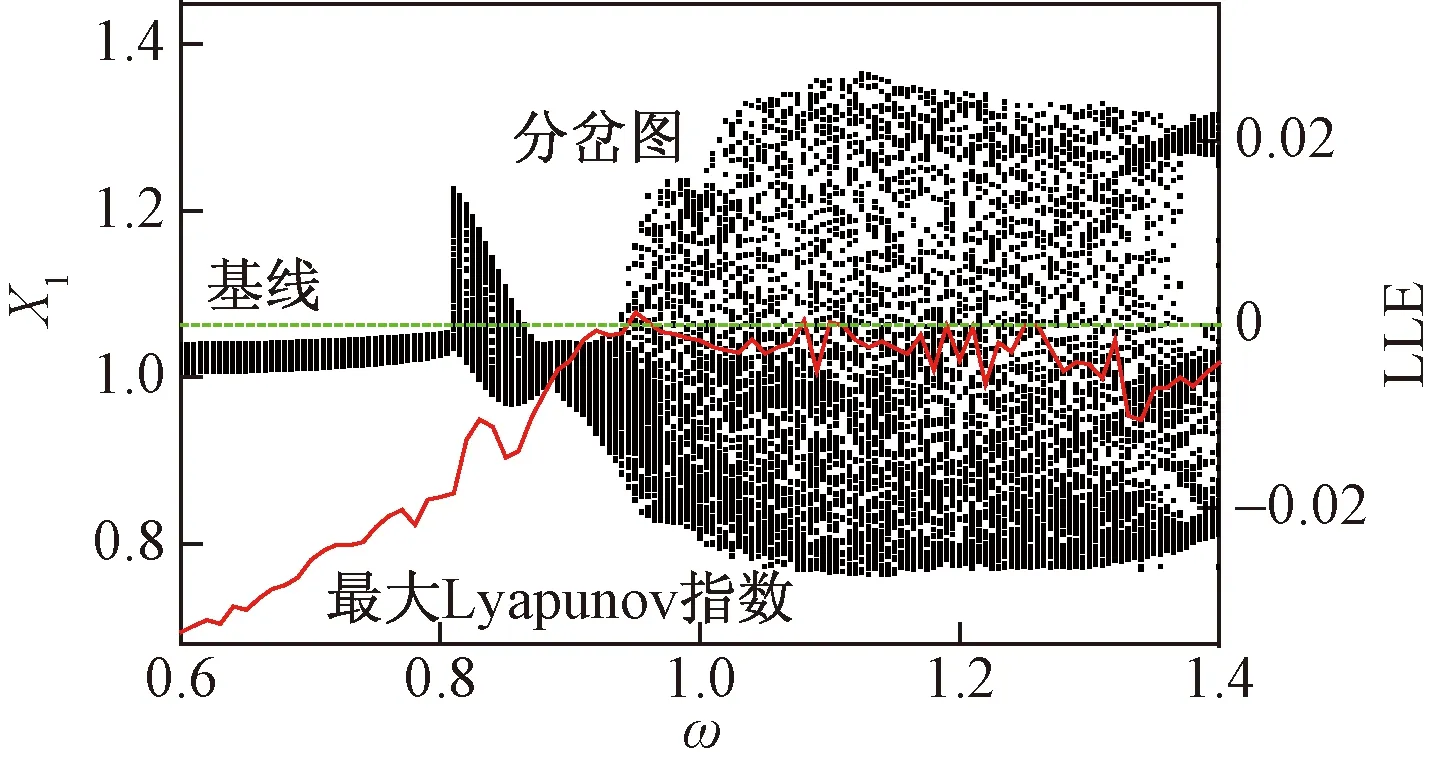
图7 垂荡运动下附加气囊-浮筏隔振装置的转子系统在α=0.1时的分岔图及最大Lyapunov指数Fig.7 Bifurcation diagram and largest Lyapunov exponents of rotor system with air bag-floating raft vibration isolator under heaving motion when α=0.1

表3 隔振装置对转子系统动力学分岔特性的影响

2.2 隔振装置耦合转子系统动力学分析

图8为参数α=0.1，σ=3，ν=[30,70]，Ah=120，n=7.5，K=9，D=0.2时，附加气囊-浮筏隔振装置的转子系统在船体垂荡运动下的轴心轨迹。由图8可见，初始时随着转速不断增加，转子系统的位移不断增大；而在ω从0.95到1.3时，转子的位移增大趋势不再明显，但转子的轴心轨迹重合程度较低，且占据很大范围，转子系统运动十分复杂；而在高转速时，转子轴心轨迹的重合程度有所提高，预示着转子运动的复杂程度有所降低。

图9为船体垂荡运动下附加气囊-浮筏隔振装置的转子系统在转速变化时结合多种方法分析的系统动力学响应。结合对应的最大Lyapunov指数(LLE)将分析结果在表4中列出。

图8 不同转速下转子的轴心轨迹Fig.8 The rotor orbit at different speeds

图9 转子-隔振系统的稳态响应Fig.9 The steady-state response of rotor-vibration isolation system when

表4 隔振装置耦合转子系统的动力学特性

3 结论

建立了船体垂荡运动条件下，具有气囊-浮筏隔振装置的转子-轴承系统的运动方程。运用数值方法讨论了该系统的非线性振动特性，并分析了气囊-浮筏隔振装置对转子系统振动的抑制效果。结果表明：转速较低时，转子系统处于拟周期状态，随转子转速的增加，系统交替出现拟周期和混沌运动，在高转速时，转子系统返回拟周期运动状态。在较宽的转速范围内，气囊-浮筏隔振装置对系统振幅的增加具有明显的限制和滞后效果。且在中、高转速时，气囊-浮筏隔振装置能够延后和限制转子系统进入混沌运动状态。以上结论有助于揭示垂荡运动下，气囊-浮筏隔振装置耦合转子-轴承系统的运动规律，并为船用转子-隔振系统的动力学设计和振动控制提供理论依据和研究方法。