全速率准正交空时码的低复杂度编译码算法设计

薛银泉, 侯 嘉

(苏州大学电子信息学院，苏州 215006)

空时分组码(space time block code, STBC)是多输入多输出(multiple-input multiple-output, MIMO)系统中相对较容易实现且可以获得较高分集增益的一种编码方式，是支撑当下高速率和高业务质量宽带无线通信的先进技术之一。为了提高STBC的传输速率与分集增益，不少文献都提出了一些更高效的空时分组码设计方案。文献[1]针对两根发射天线一根接收天线的2×1 MIMO系统，提出了一种全速率全分集低译码复杂度的正交空时分组编码(orthogonal space time block code，OSTBC)。文献[2]则是将文献[1]中代码应用在短波通信中，提升通信的可靠性。文献[3]在文献[1]的基础上，针对两根发射天线两根接收天线的2×2 MIMO系统，提出了一种全速率全分集和低译码复杂度的OSTBC (VH码)，提高了传输效率。针对四根发射天线一根接收天线的4×1 MIMO系统，文献[4]率先提出了一种简单的全速率准正交空时分组编码(quasi-orthogonal space time block code，QOSTBC)的设计方案，但是该方案并没有形成全分集，且译码复杂度较高。因此在文献[4]的基础上，文献[5-6]通过使用调制信号星座图旋转，获得了全速率和全分集的QOSTBC设计结果，但译码复杂度仍然没有改善。所以文献[7-8]又分别在文献[5]的编码方案基础上，进一步使用基于有条件的最大似然(conditional maximum-likelihood，CML)译码算法和干扰消除(successive interference cancelation，SIC)算法成功降低了译码复杂度。文献[9]将QOSTBC应用在下行MIMO和稀疏码多址接入(sparse code multiple access，SCMA)中，提升了传输性能。为了提高传输效率，采用四根发射天线二根接收天线的4×2 MIMO系统的全速率和全分集QOSTBC设计方案后续被文献[10-13]提出，这些方案在取得更高速率编码增益的同时，被发现通过编码结构的改善也能降低译码的复杂度，如文献[10]中的BHV(biglieri-hong-viterbo)编码通过将两个文献[4]中的QOSTBC进行线性组合得到了更高速率设计方案，但没能达到全分集的效果；而文献[11]中的IFS(ismail-fiorina-sari) 编码和文献[12]中的SR(srinath-rajan) 编码在线性扩展的基础上结合交错正交设计，分别提出了新的全速率全分集且低译码复杂度的QOSTBC设计方案；接着，文献[13]中的LHHC(Liu-Hélard-Hélard-Crussière)编码在全速率和全分集的条件下进一步通过编码设计降低了译码复杂度；这其中SR编码和LHHC编码都获得了最大的理论编码增益。而文献[14]在分布式MIMO中综合应用了BHV码、IFS码和SR码，获得了高传输效率的性能结果。

基于此，现进行4×2 MIMO空时编译码设计，使其具有与现存方案至少一致的编码增益，同时通过低复杂度译码算法，进一步有效降低计算复杂度。

1 系统模型

模型假设在接收端已知信道状态信息(channel state information，CSI)情况下，接收信号可以表示为

Y=HX+N

(1)

式(1)中：X∈CNt T为发射信号编码矩阵；T为发射编码矩阵的时隙数，T=4；Nt为发射天线数目，Nt=4；H∈CNr Nt为瑞利衰落信道，Nr为接收天线数目，Nr=2；N∈CNr T为符合分布(0,N0)的复高斯白噪声，N0为高斯白噪声的方差。

定义1若STBC编码矩阵中有K个信息符号，且传输速率K/T=min(Nt,Nr), 则称为全速率编码[8]。因此在4×2 MIMO系统全速率编码设计方案中，传输速率为2。

由于X为复数编码矩阵，因此可以表示为实部和虚部相分离的表达形式[11]：

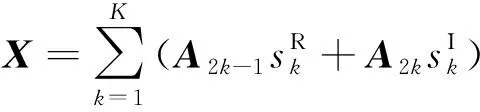
(2)

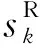
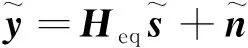
(3)

(4)

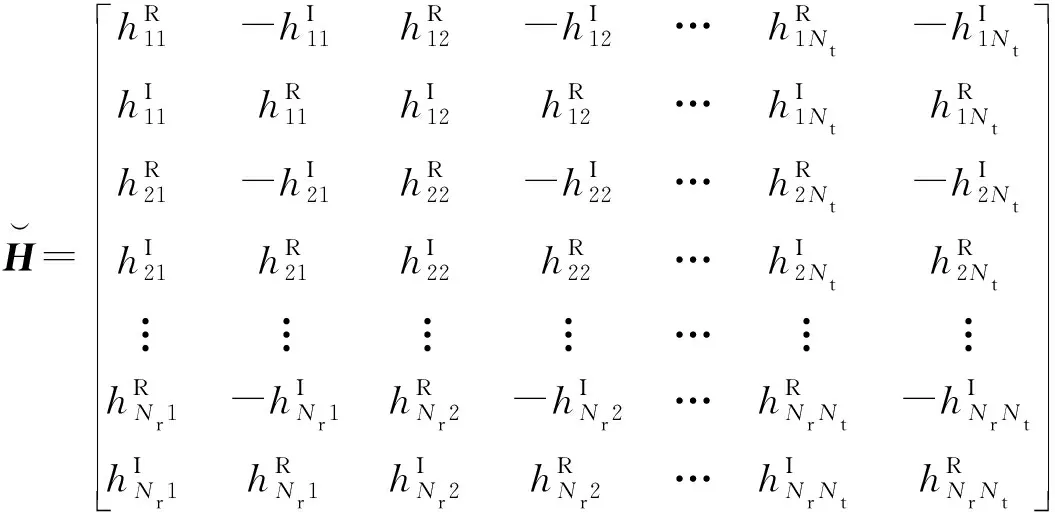
(5)

而实虚部分解的等效编码矩阵G表示为

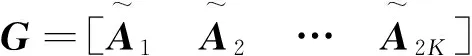
(6)

定义2行列式值判定标准，对于一个满秩的STBC，它的最小行列式值[12]定义为

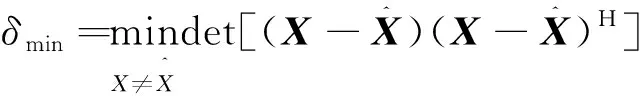
(7)

式(7)中：( )H为共轭转置，而该编码增益可以表示为(δmin)1/Nt，因此本文算法就是通过选择合适的参数，使所提编码方案的增益最大化，不低于现有的最优理论值。

2 准正交空时编码设计方案

文献[15]首先提供了一种4根传输天线的准正交空时编码QOSTBC设计方案，具体如下：

X1234=

(8)

很明显，根据定义1，此编码的传输速率仅为1，且不具备全分集增益。因此，在此基础上使用优化旋转因子可以得到全分集编码方案[12]：

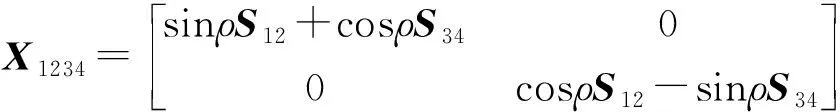
(9)

式(9)中：S12和S34均为传统的Alamouti码。

(10)

X=(X1234+eiθX5678P)T

(11)

式(11)中：X1234和X5678同式(9)的方案，而增加的旋转因子角度θ=π/4，置换矩阵P可表示为

(12)

本文编码方案在全分集的基础上，根据定义1，其传输速率为2。在MATLAB仿真软件中，使用未归一化的QAM星座调制信号条件，依据定义2和式(7)，对编码行列式进行计算，结果表明，本文的编码方案具有与SR码和LHHC码一样的最小行列式值δmin=10.24，且最优编码增益可计算为(δmin)1/Nt=1.789。四种不同编码方案在同一条件下具体计算结果如表1所示，与现有文献中的最优编码方案的计算结果一致。

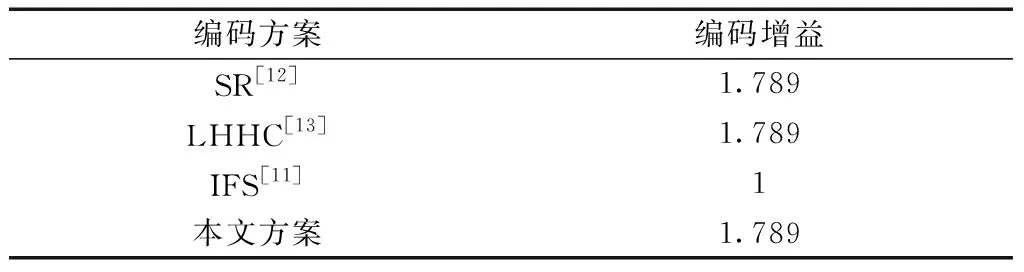
表1 编码增益计算结果

3 低复杂度译码算法

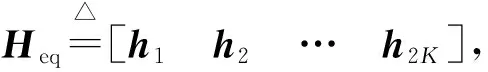
Q=[q1q2…q2K]

(13)

和

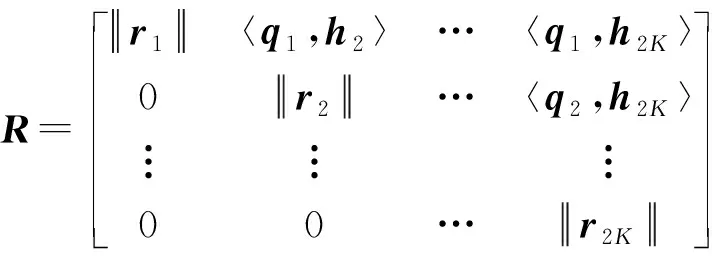
(14)

(15)

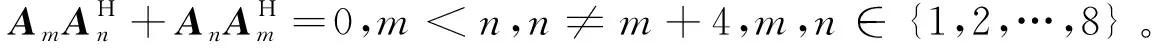
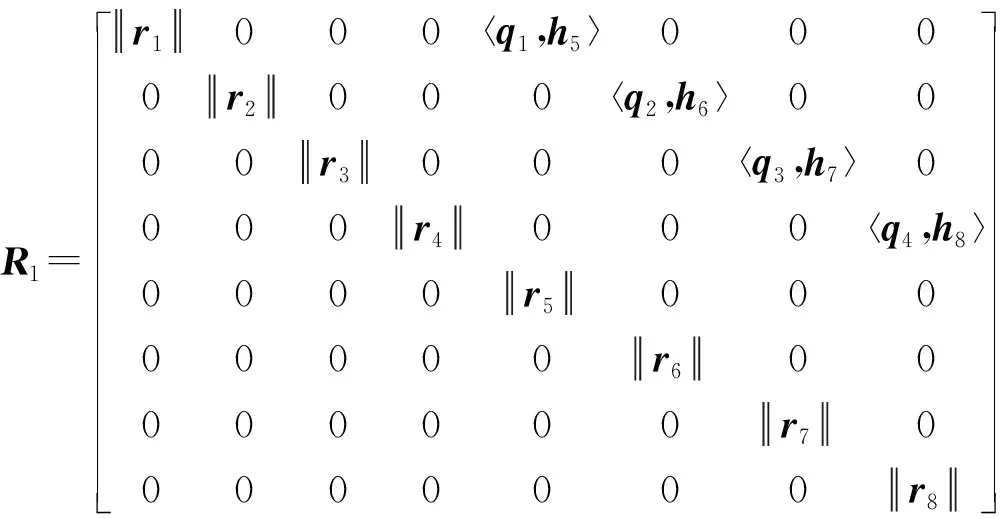
(16)

接着，在式(3)两边同时乘以QT，可以得到

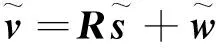
(17)

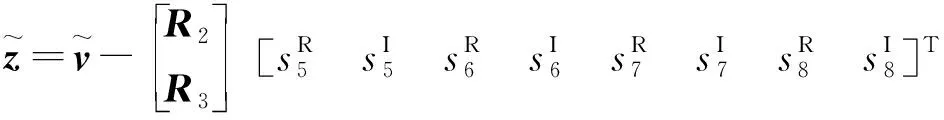
(18)

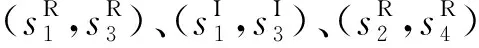
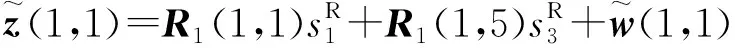
(19)

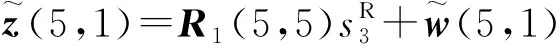
(20)

在M-QAM调制下，采用SIC算法首先可得到简化的硬判决结果为[12]

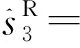
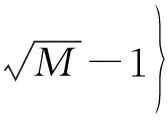
(21)

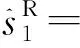
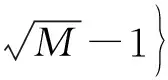
(22)

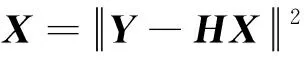
(23)

4 译码算法复杂度计算结果

对于4×2准正交空时编码方案的译码算法，时隙数T=4，信息符号数K=8，计算方法如下：第一步：预处理算法中Heq的实数加法与乘法运算次数分别为4KTNr(2TNt-1)和8T2KNrNt+4T2NrNt；第二步：QR分解需要的实数加法与乘法次数分别为(4TNr-1)(2K-1)K+2(2TNr-1)K和4KTNr(2K+1)；第三步：QT相乘处理的实数加法与乘法次数分别为2K(2TNr-1)和4KTNr；第四步：简化硬判决的实数加法与乘法次数可分别表示为(2K2+K+39)M4和(2K2+K+44)M4。

表2详细列出了本文编码方案的译码算法与文献[13]中译码算法的实数加法和乘法运算次数的计算结果。结果表明，本文编码方案的译码算法复杂度有所降低，尤其是在越高阶星座图中，降低的效果更加明显。

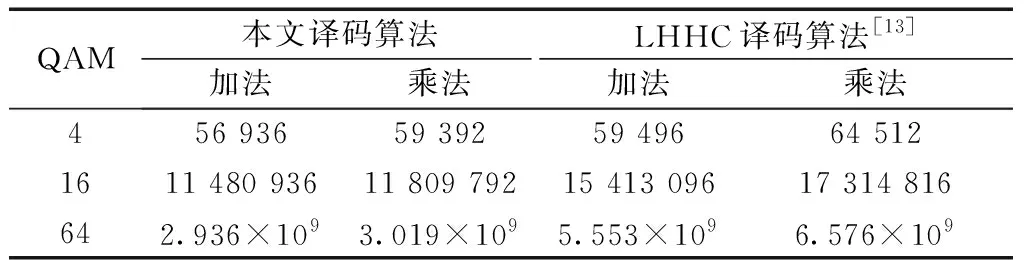
表2 加法与乘法次数

从表2中可以看出，在4-QAM调制信号条件下加法和乘法运算次数分别降低了4.3%和7.9%，在16-QAM调制信号条件下加法和乘法运算次数分别降低了25.5%和31.8%，在64-QAM调制信号条件下加法和乘法运算次数分别降低了47.1%和54.1%。

5 仿真结果与分析

本文方案使用4×2MIMO准静态平坦瑞利衰落信道。图1(a)和图1(b)分别是在4-QAM和16-QAM下，本文方案与其他现有方案译码算法之间的误码率(bit error rate, BER)比较，横坐标为每个符号对应的信噪比，纵坐标为符号转换为二进制后的误码率。从图1中可以看出，本文方案可以获得最佳误码率性能，该性能与LHHC码和SR码性能一致。与该方案具有最大编码增益的结果相一致。

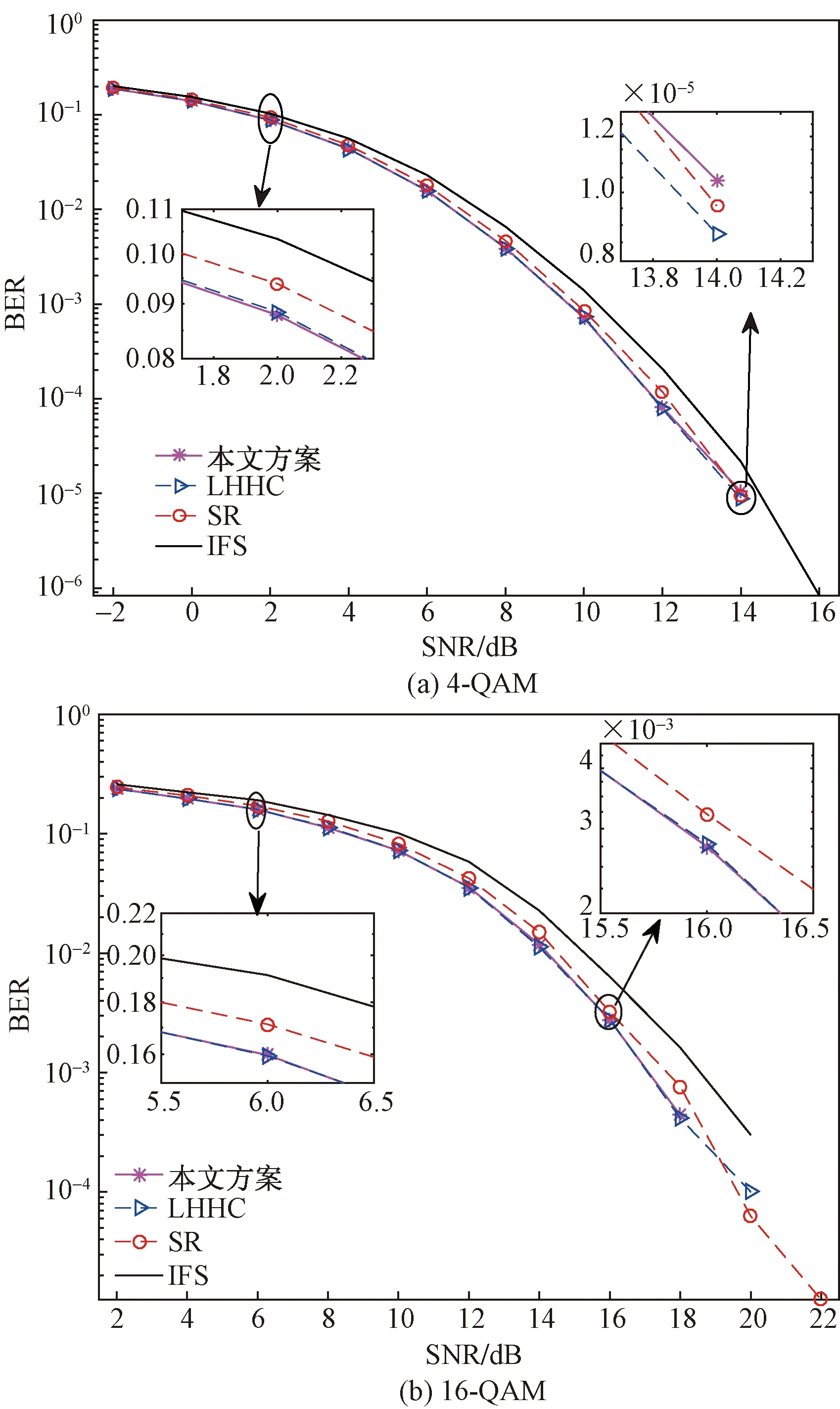
图1 不同方案误码率比较Fig.1 BER comparison of different schemes

图2(a)和图2(b)分别是在4-QAM和16-QAM下，将本文方案的译码算法和文献[13]STBC方案译码算法以及其BER性能进行比较，横坐标为每个符号对应的信噪比，纵坐标为符号转换为二进制后的误码率。从图2可以看出，本文方案误码率性能在低信噪比时与文献[13]中译码算法的BER性能一致，在高信噪比时，BER性能略微降低，差别很小。

由图2(a)可以看出，在4-QAM调制信号条件下，本文方案的性能与最优的LHHC码的性能基本一致，在部分信噪比条件下略差一点，且这一差别的最大差值仅约为0.2 dB。而由图2(b)也可以看出，在16-QAM调制信号条件下，两种方案的性能差别更小，最大差值基本小于0.1 dB。这验证了本文方案能基本达到最优的LHHC码的性能，在性能相近的情况下降低了译码复杂度。由表2计算可以得到，在4-QAM调制信号条件下，本文方案的加法和乘法运算次数能分别降低 4.3%和7.9%; 在16-QAM调制条件下，所提译码算法的加法和乘法运算次数分别降低了25.5%和31.8%。

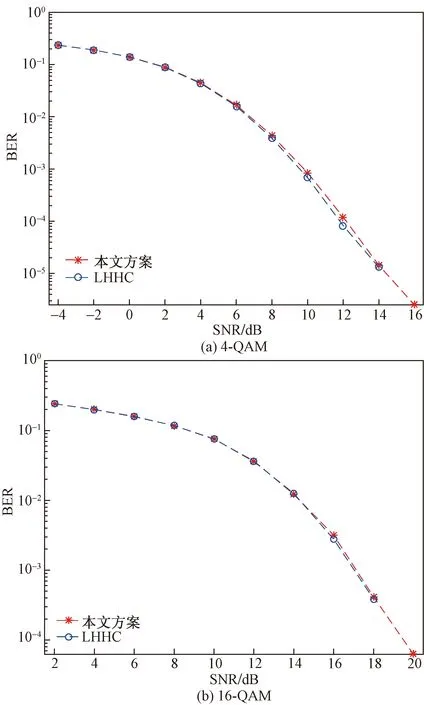
图2 本文方案与文献[13]中译码算法比较Fig.2 The comparison of the proposed decoding algorithm and the decoding algorithm in ref[13]

除了和理论编码增益最大的LHHC码和SR码的性能比较之外，图3(a)和图3(b)还分别给出了本文方案与VH码[3]和EMM算法[7]的比较分析结果。首先从图3(a)可以看出，在不同的调制情况下(4-QAM和16-QAM)，本文方案性能均远远高于VH码。

从图3(b)也可以看出，在不同调制情况下(4-QAM和16-QAM)，本文方案在低信噪比时性能会略差于文献[7]中的EMM算法，但是在高信噪比时性能都优于EMM算法，且传输效率要更高一些。

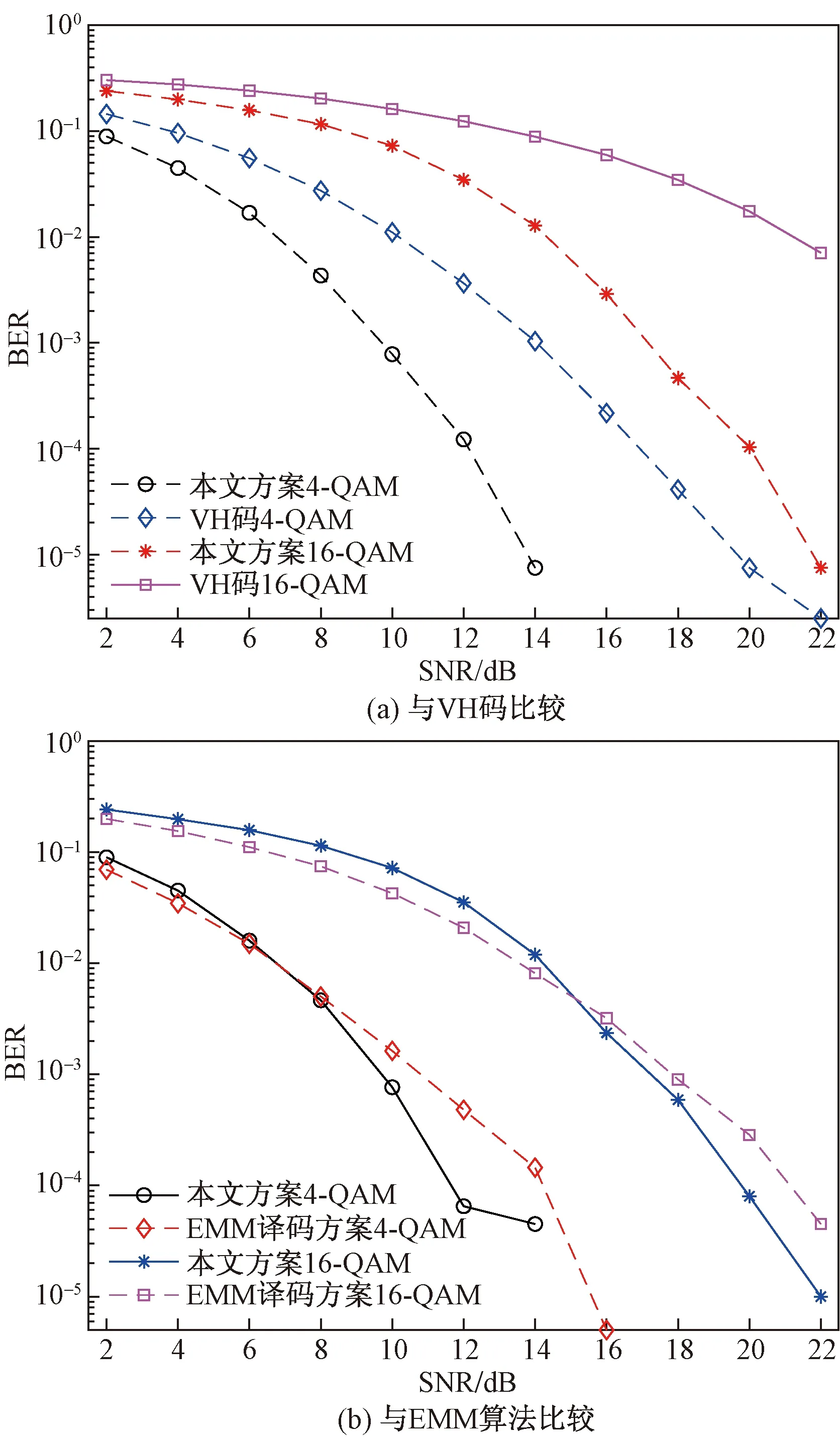
图3 本文方案与VH码和EMM算法误码率比较Fig.3 BER comparison of the proposed encoding and decoding scheme with VH and EMM

6 结论

针对4×2MIMO系统提出了一种具有全速率、全分集、高编码增益的STBC方案，丰富了现有的优化编码方案。在使用文献[13]译码算法时，该编码方案可以获得与SR码和LHHC码一样的性能。同时，还根据本文方案获得了低复杂度的译码算法，当使用该算法时，不仅可以获得与其他方案相近的译码性能，还可以进一步减少计算次数，尤其是在高阶星座图调制情况下，计算次数会随着阶数的增加降低的比例越大。这将有助于在未来的研究中，将本文方案与多天线中继协助相结合[16]，进行低复杂度的系统设计。