基于乳房形态特征的义乳曲面建模与体积预测

罗火静，刘 驰，徐步高

(1.西安工程大学 服装与艺术设计学院，陕西 西安 710048;2.北德克萨斯大学 营销与数字零售系，美国 丹顿 311100)

0 引 言

乳腺癌发病率逐年提高[1]，失乳人群逐年增加[2]。患者术后的生活质量引起广泛关注[3]，失乳人群由于乳房缺失产生自卑、抑郁的情绪[4-6]。为缓解生理及心理压力[7-8]，提高生活质量，患者常常选择佩戴义乳及义乳文胸[9-12]。现阶段对义乳的研究主要集中在义乳的认知度和佩戴情况[13-14]、患者穿着心理[15]和穿着舒适性[16-18]的调查上。调查发现，义乳形状、质量不能匹配原乳房，造成穿着不舒适。为改善义乳的穿着舒适性，提出对义乳的形态进行设计研究。

逆向工程在人体工程研究方面应用广泛，研究主题包括人体体型研究[19-21]和人体模型的重构[22-24]，通过逆向工程进行的人体重构模型效果良好，因此选取逆向工程技术对义乳曲面模型进行重构。乳房体积的测量方法有实验法、影像法和人体数据测量法[25]。人体数据测量法是利用人体数据，通过回归分析建立乳房体积与人体数据间的线性关系模型。BROWN和QIAO等采用将乳房近似为圆锥体的方式计算乳房体积[26-27]；马静运用逐步回归模型，建立乳房体积与乳房弧线、胸围差间的回归方程[28]；LONGO等利用多元回归，建立BREAST-V乳房体积预测公式[29]。但这些方法建立的乳房体积模型为线性回归模型，拟合度较差。

基于乳房形态特征参数进行义乳形状与体积的设计。首先提取用于义乳设计的乳房特征参数，数据来源于通过三维人体扫描仪测量得到的122位女性测量数据，从乳房形态数据中提取共性，再用于指导义乳形态的设计。义乳的形态包括形状和体积，义乳形状设计是运用逆向工程参数化建模方式，建立曲面模型；义乳体积的计算通过BP神经网络，采用义乳特征参数，建立体积预测模型。

1 乳房形态特征参数提取

1.1 数据获取

使用三维人体扫描仪，对122位女性进行人体扫描，获得乳房形态点云数据。选取与乳房形状相关的乳房根围线、上/下/前/侧奶杯弧线/直线/垂线距、乳间距、乳房深度等15个参数，对每位测量对象的每个测量部位进行测量。

过乳房上/下缘点、心位点、侧位点等4个点建立乳房切除平面，将乳房切除，计算切除的乳房体积。此切除方式也运用于对乳房的义乳形态设计过程。

1.2 乳房形状特征参数

运用SPPS数据分析软件对描述乳房形状特征的15个参数进行主成分分析。主成分分析总方差见表1。各主成分特征值分布比较理想，提取特征值大于1的主成分用于描述乳房形状特征。共提取3个主成分，其累积方差为85.093%。

表1 主成分分析总方差

对提取的3个主成分旋转后的成分矩阵进行分析，从每个主成分中提取出占比最高，描述乳房形态特征最具代表性的参数。从3个主成分中，共提取出6个与乳房形状相关性最高的参数，分别为上乳杯弧长、下乳杯弧长、前侧乳杯弧长、侧乳杯弧长、乳房根围和乳房深度。

1.3 乳房体积特征参数

通过乳房形状特征参数预测乳房体积,运用SPSS软件对特征参数与体积间的相关性进行Pearson相关性分析，主成分分析总方差结果见表2。乳房体积与6个乳房形状特征参数间皆显著相关。因此，可以通过乳房的形状特征参数预测乳房的体积。

表2 左乳体积Pearson相关性分析表

2 义乳形态设计

2.1 义乳形态原模型

以乳房上缘点、乳房下缘点、心位点和侧位点4个点建立的平面作为切除平面，进行乳房切除。由于实验对象为标准人台，切除的乳房形状类似水滴状，故称为水滴型义乳。

2.2 义乳形状曲面模型

2.2.1 特征点与特征曲线 特征点位置及象限分割如图1所示。设BP点在切除平面的投影点为BP′，心位点、乳房根围最低点、侧位点、乳房上缘点分别用A、B、C、D表示，以BP′为原点，切除平面为基准面，BP′→A、BP′→D、BP′→BP的直线方向为X、Y、Z轴的正方向，建立三维坐标系。

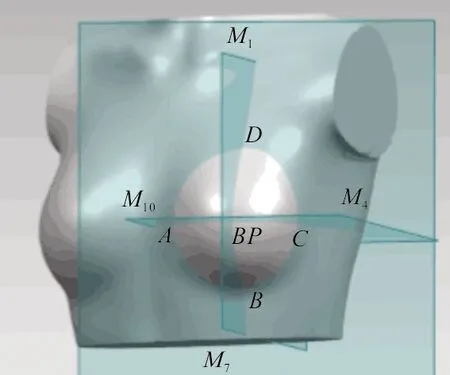
图1 特征点位置及象限分割

参照医学上对乳房的象限划分方法，过BP点设置水平与垂直切面，分割面与乳房平面相交线即提取的乳房特征参数曲线。将分割面以30°为角距均匀旋转，插入分割面。将所有的分割平面按顺时针方向命名为M1，M2，…，M12。

沿Z轴正方向，以切除平面N1为依据，在乳晕处插入平行平面，在基准平面与乳晕平面之间再均匀插入5个截面，将乳房分为6层。沿Z轴正方向将分层平面依次命名为N1，N2，…，N7，各截面与乳房相交形成7条环形曲线。

平面Ni(i=1，2,…,7)与平面Mj(j=1，2,…,12)相交，映射在乳房表面形成型值点，将型值点命名为Pij(i=1，2,…,7；j=1，2,…,12)，i表示该点所在的分层平面，j表示该点所在的分割平面；共形成84个型值点。义乳型值点如图2所示。

图2 义乳型值点

设BP′点到A、B、C、D的距离分别为a、b、c、d，乳深为h，Pij的x坐标值为xj。Pij的y坐标值用xj的线性关系式表示；每一个分层平面z值相等。对型值点的点坐标进行参数化表示，义乳表面型值点参数化坐标见表3。

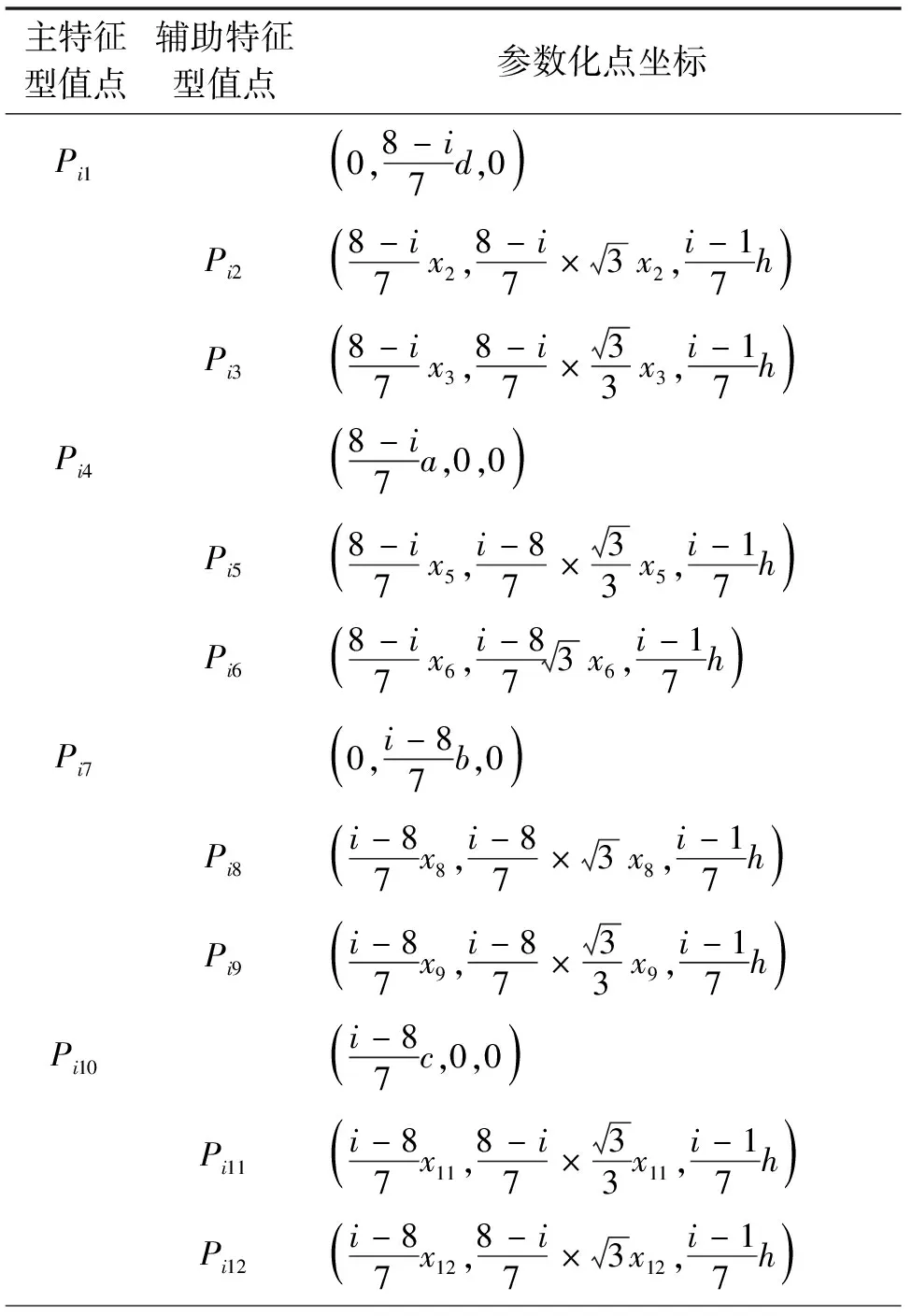
表3 义乳表面型值点参数化坐标

义乳的曲面设计可通过改变型值点的坐标来实现。义乳曲面建模以型值点为基础，由点到线，再由线到面。

2.2.2 水滴型义乳参数化曲线模型 将每2个型值点以3次参数样条的形式连接，形成曲线段。3次参数样条曲线的表达式为P(t)=Bs+Bst+Bst2+Bst3(0≤t≤tm)。每一分层平面的第几段曲线用m(m表示点j和点j+1之间的曲线)表示，每一分割层的第几段曲线用n(n表示点i和点i+1之间的曲线)表示。将分层平面的曲线段表示为Fi，m(t)，(i=1，2,…7；m=1，2,…,12)。将分割平面上的曲线段表示为Gj，n(t)，(j=1，2,…，12；n=1，2,…，7)。则

Fi，m(t)=Bs+Bs+1t+Bs+2t2+Bs+3t3，

0≤t≤ts

(1)

依据3次参数样条曲线的定义、端点性质、方向性质，求解得到曲线段表达式为

Fi，m(t)=Pi，m+P′i，mt+

(0≤t≤tm+1)

(2)

(0≤t≤tn+1)

(3)

使用3次参数样条曲线连接型值点，绘制义乳形状曲线，得到的7×12条水滴型义乳曲线模型如图3所示。

图3 水滴型义乳参数化曲线模型

2.2.3 水滴型义乳参数化曲面模型 利用双三次参数曲面模型建立义乳曲面。义乳外表面共形成72个曲面片。建立乳点曲面。在每一条分割线无限接近乳点的位置切入2条线，用于构建曲面片。共形成84个曲面网格。分层曲线段和分割曲线段形成的网格如图4所示。

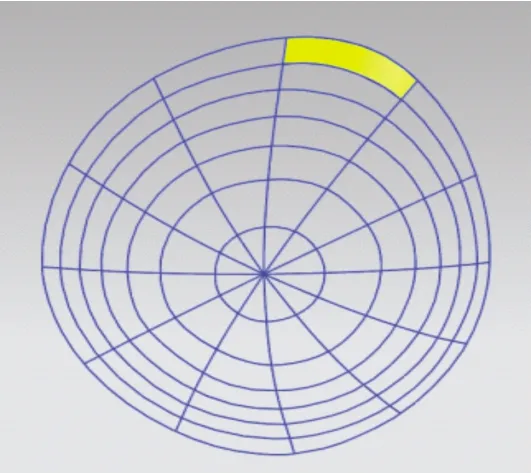
图4 分层曲线段和分割曲线段形成的网格

在每一格曲面片中，由4条边界曲线函数生成一个曲面，用S(u，v)表示曲面，表达式为

其中

用(F(t)v)i，a表示分层方向上的切矢量，(G(t)u)j，b表示分割方向上的切矢量，(F(t)v)i，a(G(t)u)j，b为扭矢量,则Q矩阵为

Q=(Q1,Q2,Q3,Q4)T

式中：

Q1=(Pi，j,Pi，j+1,(F(t)v)i，a,(F(t)v)i，a+1)

Q2=(Pi+1，j,Pi+1，j+1,(F(t)v)i+1，a，

(F(t)v)i+1，a+1)

Q3=((G(t)u)j，b,(G(t)u)j，b+1,

(F(t)v)i，a(G(t)u)j，b,

(F(t)v)i，a+1(G(t)u)j，b+1)

Q4=(G(t)u)j+1，b,(G(t)u)j+1，b+1,

(F(t)v)i+1，a(G(t)uj+1，b,

(F(t)v)i+1，a+1(G(t)u)j+1，b+1)

将每一个曲面片按张量积的方式进行曲面处理，形成84个网格曲面。将曲面进行光滑连接，形成义乳的外表面形状如图5所示。图5中，黄色为逆向工程曲面建模生成的义乳外表面曲面模型，银色为原乳房的曲面模型，黄色部分与银色部分相互融合，义乳模型与原乳房匹配度良好。

图5 水滴型义乳外表面形状图示

对义乳第一层分层曲线进行填充，形成曲面，即义乳的内表面，完成对水滴型义乳特征曲面的参数化建模。

2.3 义乳体积预测模型建立

利用义乳形状特征参数数据，采用BP神经网络，建立义乳体积预测模型。通过对比不同训练算法的优越性，选出最好的预测方案。

2.3.1 BP神经网络参数确定 义乳形状特征部位为6个，测得样本数为122份。以122×6的矩阵形式作为输入层输入到Matlab R2018a的工作区中，赋值为p；以122份样本数的体积作为输出层，赋值为t，构成122组样本组。用Randperm函数将样本组的顺序打乱，抽取100对作为训练集，22对作为测试集。设置隐含层节点数，输入层到隐含层的函数为Tansig函数，隐含层到输出层的传输函数为Purelin函数。依据不同的传递函数设置不同的训练次数epochs、最长训练时间time、性能目标goal、学习速率lr等参数值。对拟牛顿算法、梯度下降法、动量梯度下降法、Levenberg-Marquardt算法建立网络语言，进行义乳体积的预测模型训练。

2.3.2 BP神经网络训练 依据算法进行网络训练，获得义乳体积预测模型。对每种方法的训练模型结果进行说明。拟牛顿算法的网络模型在模拟40次后停止，训练速度极快。但整体拟合度只有0.893 9，拟合效果一般。

动量梯度下降法:网络模型运行至设置的最高次数后，运行停止，用时43 s；整体拟合度为0.904 91，拟合效果较好。

梯度下降法：网络模型运行至设置的最高次数后，运行停止，用时41 s，整体拟合度为0.903 58，拟合效果较好。

Levenberg-Marquardt算法：网络模型运行8次后停止，训练速度极快，整体拟合度为0.910 46，拟合效果良好。

对4种方法预测的结果值进行均值及均方误差计算(见表4)，对比4种算法的预测结果。

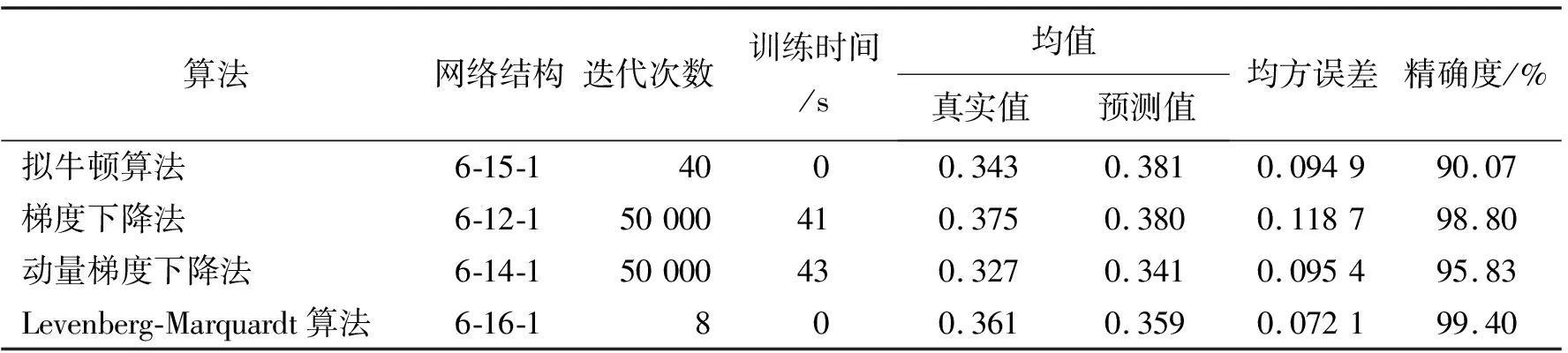
表4 4种算法预测结果对比

在对义乳体积进行预测的4种算法模型中，拟牛顿算法及Levenberg-Marquardt算法的迭代次数和训练时间比梯度下降法和动量梯度下降法少。对比4种算法预测的均值，Levenberg-Marquardt算法最高，拟合度最好；拟牛顿算法拟合度最差。均方误差值越小，代表预测精确度越高，4种算法对义乳体积预测精确度大小的排序为依次Levenberg-Marquardt算法、拟牛顿算法、动量梯度下降法、梯度下降法。对比4种方法的模拟效果发现，Levenberg-Marquardt算法迭代次数最少，耗时最少，预测精确度为99.40%，模拟效果最好。

3 结 论

1)对义乳穿着过程中出现的义乳形状、质量与乳房的形状、质量不匹配造成的穿着不舒适问题，提出基于乳房形态特征的义乳形态设计研究，用于改善义乳的穿着舒适度。通过测量122位正常女性的乳房特征数据，提取义乳形态设计特征参数，即运用数据分析找到共性。选取女性人台作为实验对象，依据特征参数，进行个性化的义乳形态设计。

2)对义乳形状的设计采用逆向工程的方式。对切除的乳房进行逆向曲面建模，对曲面形状设计的特征点、特征曲线和曲面进行参数化设计，对比乳房曲面与义乳曲面的重合度，验证义乳曲面建模的效果。

3)利用义乳形状特征参数预测义乳体积，运用BP神经网络，建立多种算法预测模型，发现Levenberg-Marquardt算法预测准确率高，预测效果好。

4)义乳形态的设计，为义乳配合义乳文胸穿着，提高义乳及义乳文胸整体的穿着舒适度提供理论依据。