基于传递矩阵的平顶直墙地铁车站横向管棚受力变形计算方法研究

宋卓华， 董立朋， 陶连金,*， 赵 旭， 张 宇

(1. 北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124；2. 中铁隧道局集团有限公司， 广东 广州 511458)

0 引言

管棚支护是地下空间施工中常见的一种辅助工法，常被用来稳定拱顶及掌子面、超前加固地层，减小施工中岩土扰动以及对周围既有地下结构的影响[1]。地铁车站也常采用管棚法施工，即利用车站上层先行导洞打设横向密布管幕，形成一个能抵御上部土体荷载的支护结构，然后在管棚保护下进行车站后续施工，如北京地铁19号线右安门外站工程[2]、北京地铁19号线平安里车站工程[3]等。

针对管棚工法的分析理论，目前已有较多研究。周顺华[4]通过原位观测和室内土工离心模拟试验分析了管棚工作机制，提出了管棚工作的"棚架原理"。陶连金等[5]采用现场原位试验的方法研究了砂卵石地层中管幕施工的施工工艺和对既有结构变形的影响，发现管幕施工对土层的扰动相对较小且以沉降为主，距离管幕越远的土体受扰动越弱。孙旻等[6]将管幕简化为板，对管幕支护下的施工过程进行了数值模拟，研究了地表沉降与周围岩土体位移的变化规律，并验证了其计算方法的有效性。肖世国等[7]将管棚结构简化为固定梁与弹性地基梁，进而按梁的承载机制对箱涵顶进中管棚结构力学作用进行了分析。郑俊杰等[8]分析了掌子面前方岩土体基床系数分布规律，建立了变基床系数下的超前管棚模型，并验证了其有效性。贾金青等[9]通过建立Winkler地基模型和Pasternak地基模型，采用解析方法计算了某隧道开挖中的超前管棚受力与变形，对比了2种地基模型的计算结果，并说明了管棚的杠杆作用。李健等[10]对浅埋下穿高速公路黄土隧道管棚变形进行了监测，并采用Pasternak地基模型进行了解析计算，分析了管棚受力变形规律。

从以往研究可以看出： 对于管棚的作用机制，大部分研究都将管棚视为梁，采用"荷载-梁模型"模拟管棚，这种简化模型具有力学机制明确、计算简便的特点。但目前对管棚的计算理论研究，仍多针对平行于开挖方向的隧道超前管棚(纵向管棚)，鲜见对于平顶直墙车站暗挖PBA工法中横向管棚的力学机制研究。

针对暗挖地铁车站PBA工法施工中的密布横向管棚结构，本文首先总结了管棚"荷载-梁模型"中弹性地基梁、简支梁、固支梁3种简化方法及其计算原理；然后，依托北京地铁19号线平安里站暗挖车站工程，采用了3种简化模型分别计算管棚的受力与变形，并对不同简化模型下的计算结果进行了分析；最后，对3种简化梁模型进行了影响参数分析，总结了不同工程参数和地质参数对管棚作用效果的影响规律。

1 管棚力学模型

在进行管棚力学分析过程中，常将管棚钢管视作梁，将开挖区域上方的土体视作作用在钢管上向下的荷载，即"荷载-梁模型"。

横向管棚与开挖区域位置关系如图1所示，如果将点A简化为铰支座，此时模型即为"简支梁模型"。如果点A为固支时，模型为"固支梁模型"；如果体现点A与点B之间土体的弹性嵌固作用，则为"弹性地基梁模型"。

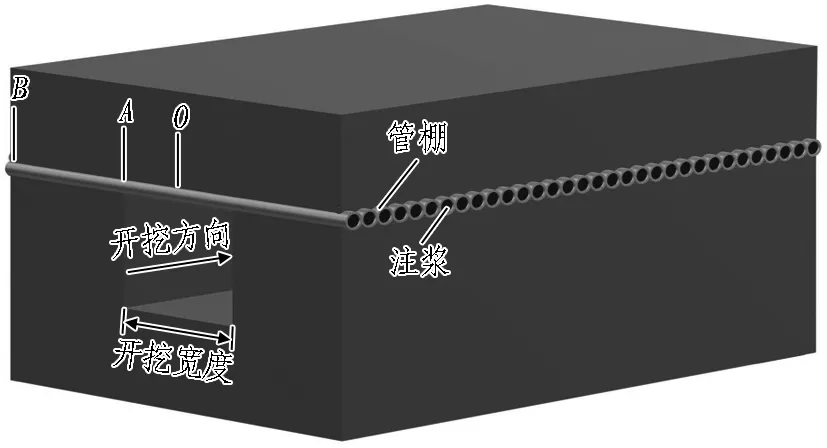
图1 横向管棚示意图

1.1 弹性地基梁

1.1.1 弹性地基梁模型

弹性地基梁模型[11]，即将管棚钢管简化为一根受弹性地基约束的梁，用土弹簧模拟土体对钢管的支撑作用，其简化计算模型如图2所示。

模型中，管幕承受上部均布荷载q作用，O为开挖导洞中点，A为开挖导洞边界，B为梁的计算边界。AB为管幕在未开挖段的长度。理论上，当AB足够长时，B点的受力和位移均趋近于0。

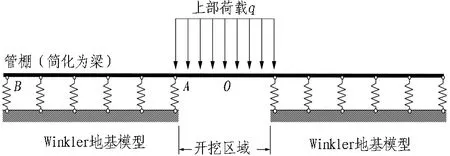
图2 管棚弹性地基梁模型示意图

1.1.2 弹性地基梁计算方法

现按照结构力学规律，只需将图2的对称结构取半进行计算。计算模型中，外荷载q作用在节点上，相邻节点之间只传递内力。节点受力示意图见图3，变形示意图见图4。

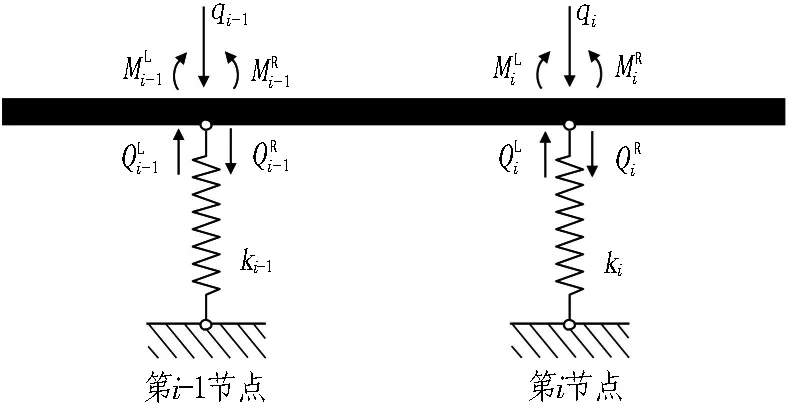
图3 计算节点受力示意图

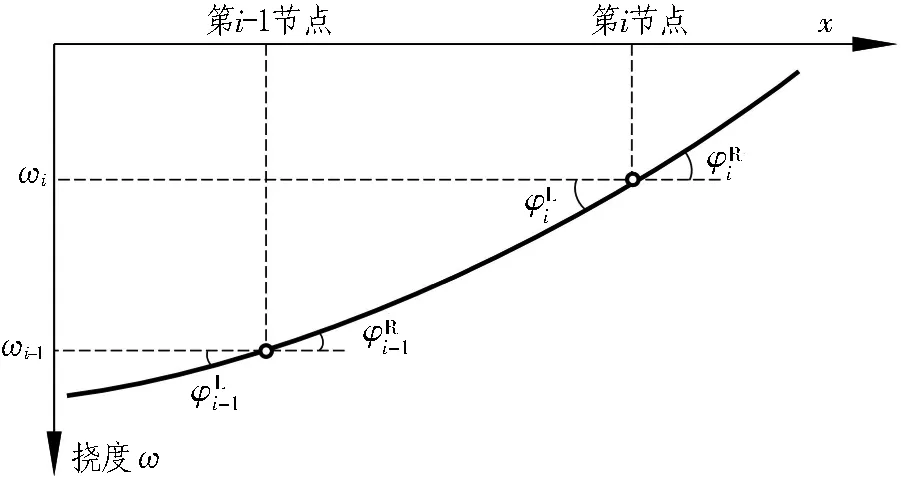
图4 计算节点变形示意图

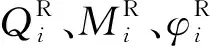
分析图3和图4中2节点之间的单元内力与节点变形传递，可得如下方程：

(1)

(2)

(3)

(4)

式(1)-(4)中：EIi为钢管的抗弯刚度；li为钢管长度。

将上述方程整理成矩阵形式，可得：

(5)

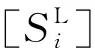
同理，根据平衡条件对节点i进行受力分析(见图3和图4)，并整理成矩阵形式，可得节点平衡方程：

(6)

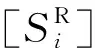
土弹簧刚度ki参考所在地层的基床系数、管棚外径和模型节点间距进行换算。基床系数可参照式(7)确定[12]：

(7)

式中：Es为土体弹性模量；μ为土体泊松比；EI为梁抗弯刚度；b为梁宽度(即钢管外径)。

由式(5)和式(6)可得：

(8)

式(8)即为从O点依次传递计算各节点内力的公式，式中[G]和[D]矩阵可以通过结构参数、荷载参数等依据式(5)和式(6)直接建立。

对于图2所示的弹性地基梁模型，其边界条件可确定为：

(9)

1.2 简支梁和固支梁模型

对于简支梁和固支梁的计算方法，只需要将图2中A点的约束条件改为简支梁、固支梁所对应的边界，如图5所示。

(a) 简支梁 (b) 固支梁

简支梁的边界条件为：

(10)

固支梁的边界条件为：

(11)

计算方法同1.1.2节弹性地基梁模型。

2 实例计算

2.1 工程概况

北京地铁19号线平安里站与6号线换乘。平安里站处于赵登禹路与平安里西大街交叉口，距地上9层、地下2层的航天金融大厦的水平距离为19.85 m，距地上5层、地下1层的平安医院的水平距离为13.33 m。赵登禹路两侧有临街商铺，距主体结构3～6 m。

车站呈南北走向，全长224.5 m，宽25.1 m，建筑面积19 190 m2，为双层3跨超浅埋平顶直墙结构，采用PBA法施工。管棚结构顶部覆土厚6.8～7.2 m，先行导洞埋深4.0～4.5 m，底板埋深20.92～21.37 m，施工范围内无地下水。

管棚施工是本项目车站主体施工的核心。从先行导洞中向东西两侧横向打设管棚，单根钢管总长35 m，向西打设18.6 m，向东打设12.4 m，在先行导洞内连通4 m。管棚施工结束后，在管棚支护作用下分别开挖上层3个导洞。车站标准横断面如图6所示。

756型紫外分光光度计，上海分析仪器厂；YP410047电子天平，上海佑科仪器仪表有限公司；DHG-9240电热恒温鼓风干燥箱，上海一恒科技有限公司；DK-SD电热恒温水槽，上海一恒科技有限公司；KQ-300DE数控超声波清洗器，昆明市超声仪器有限公司；722型可见分光光度计，上海光谱仪器有限公司；SW-CJ-IFD型超净工作台；TDL-40B-W台式低速大容量离心机，上海习仁科技仪器有限公司；远红外线食品烧烤炉。

该工程共设计钢管488根，采用φ402×16无缝钢管，打设间距为450 mm。管棚钢管之间采用角钢制作的扣件扣紧，钢管各管节之间等强焊接。钢管打设就位后在其中填充M30水泥砂浆，以提高钢管的整体抗弯刚度。

2.2 工程地质概况

平安里站周围地层分为人工堆积层、第四纪全新世沉积层、第四纪晚更新世沉积层和第三纪基岩层4层。据水文地质资料，近3～5年统计最高地下水位深约16.8 m，水质具有微腐蚀性。地质概况见图7，地质参数见表1。

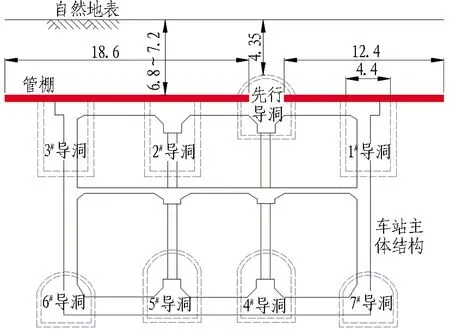
图6 平安里车站标准横断面(单位： m)

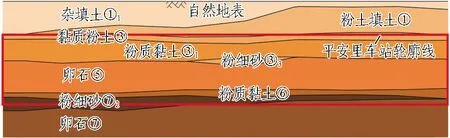
图7 平安里车站纵断面地质概况

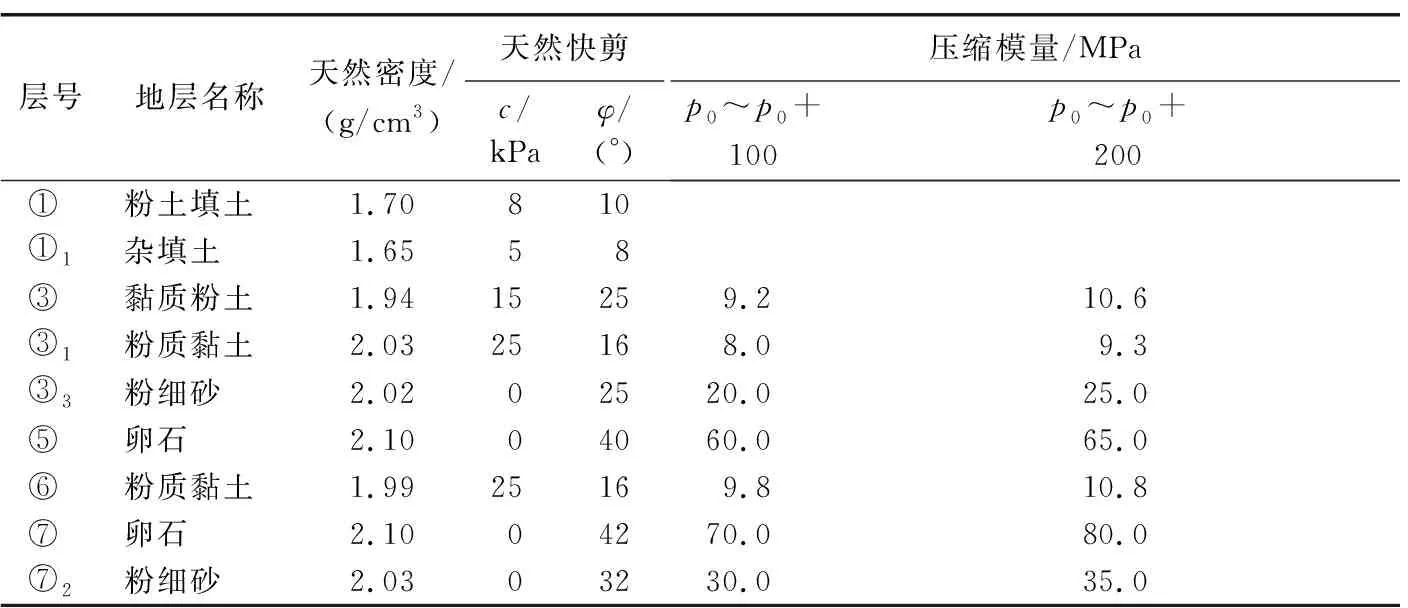
表1 平安里车站地质参数

2.3 工程监测方案

在1#导洞开挖过程中，对其拱顶沉降进行了监测。测点布置如图8所示。

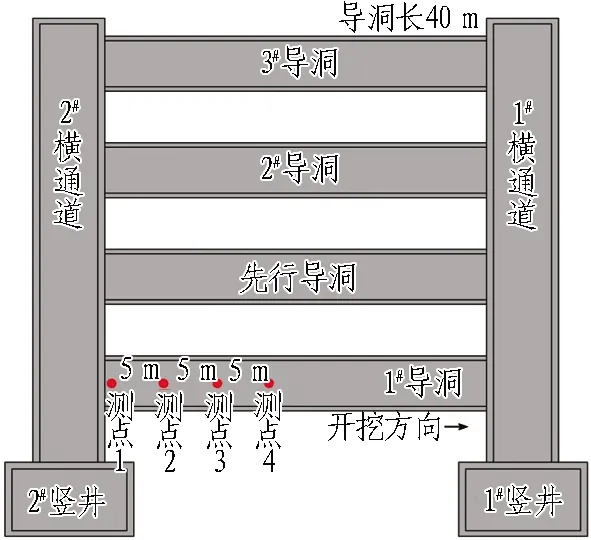
图8 1#导洞测点布置图

2.4 计算参数

对车站暗挖工程1#导洞上部管棚按照前文所述方法进行梁模型计算。参考实际施工方案，取图2的模型参数[13]如下： 梁段OA为开挖导洞范围，取OA=2.2 m；梁段AB为管棚在土体中嵌固范围，取AB=5.8 m。

管棚结构上覆土重度为20 kN/m3，覆土厚度取7 m，即单支钢管上线荷载为63 kN/m。钢管内灌注水泥砂浆弹性模量为2 GPa，钢管弹性模量为210 GPa，管棚整体等效弹性模量为60 GPa，惯性矩为0.001 26 m4，计算得等效抗弯刚度为78 000 kN·m2，土体基床系数参考实际地层取34.4 MPa/m。

2.5 计算结果与分析

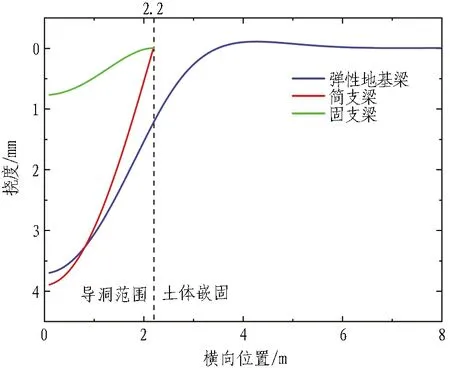
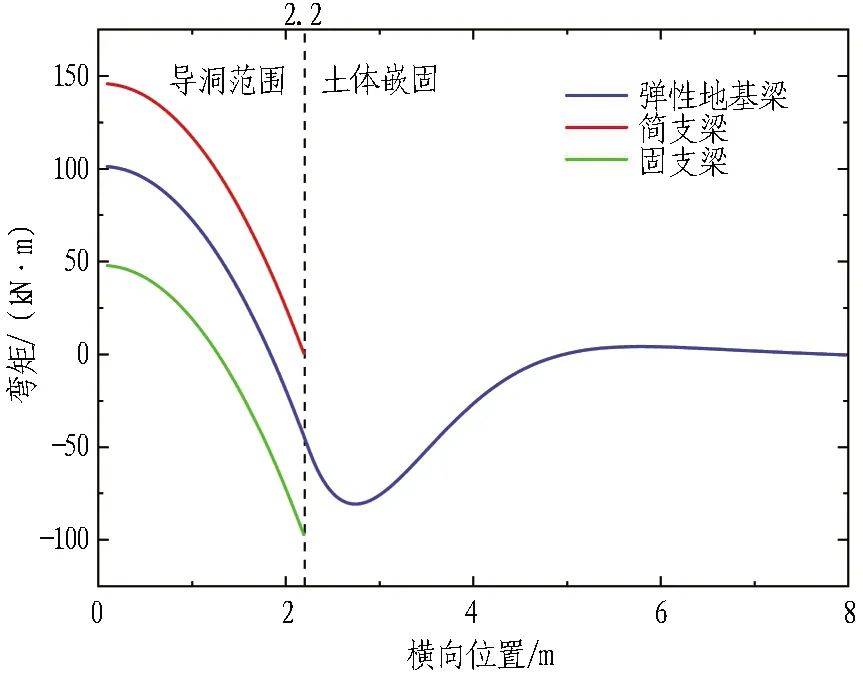
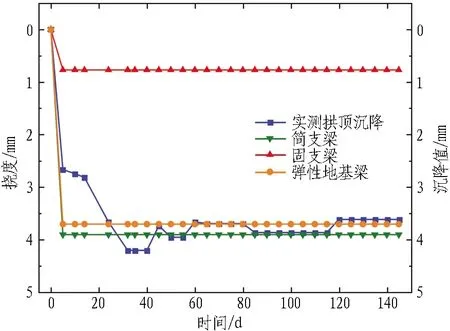
根据前文计算方法编写MATLAB计算程序。分别采用"简支梁"、"固支梁"和"弹性地基梁"3种简化方法对1#导洞开挖引起的管棚变形、弯矩进行计算，得出计算结果如图9所示。将计算结果与实测值对比，如图10所示。

(a) 挠度

(b) 弯矩

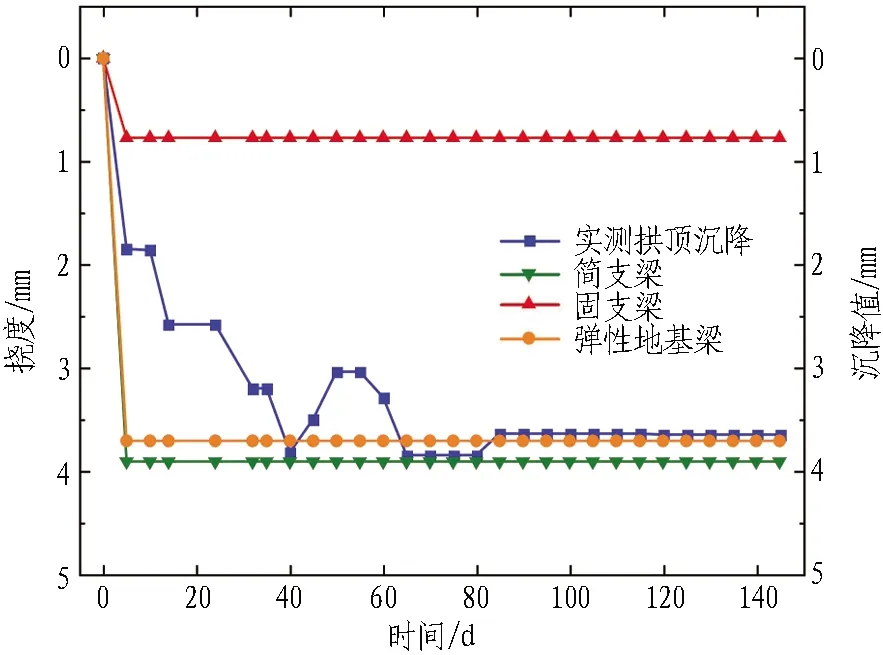
(a) 测点1

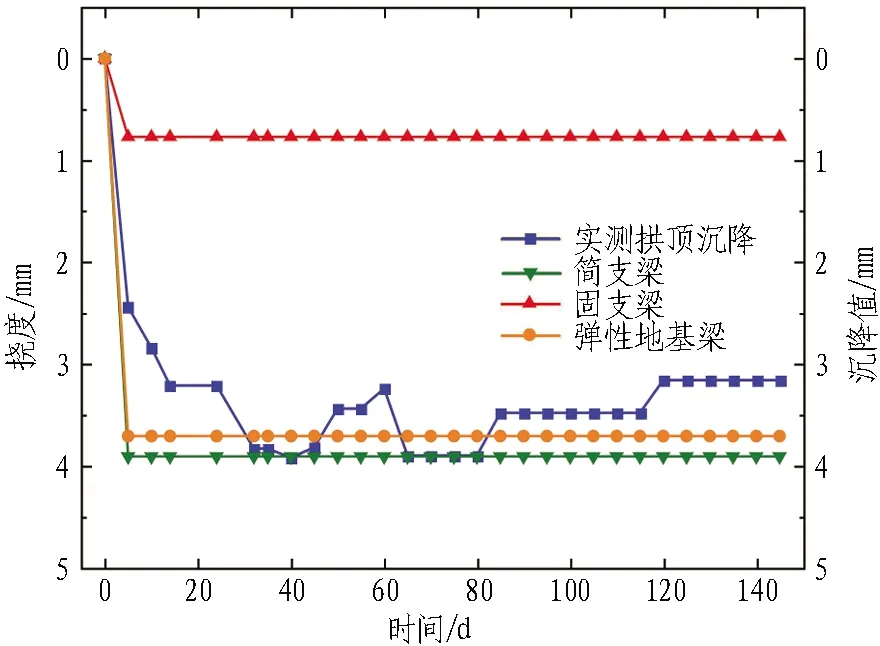
(b) 测点2

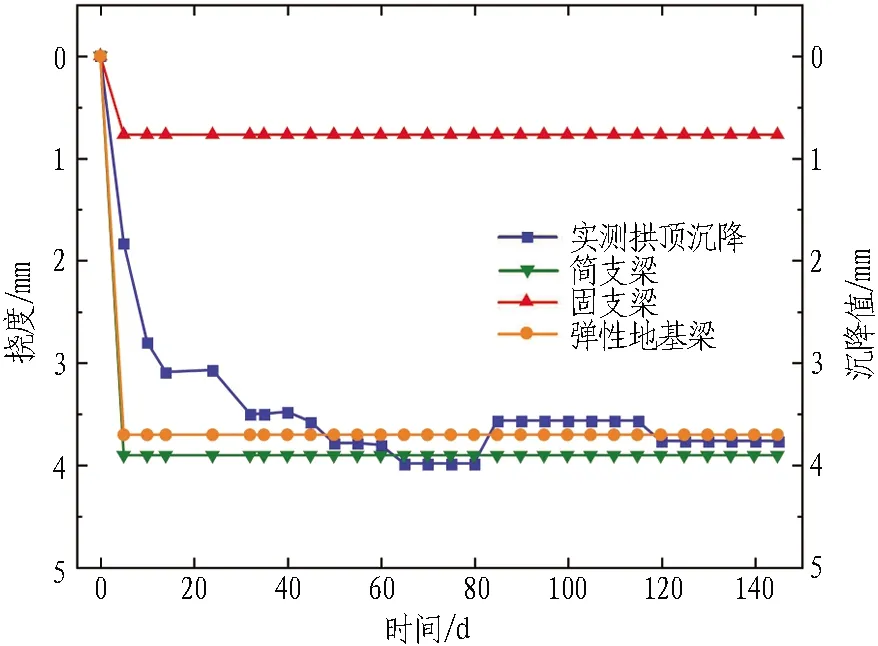
(c) 测点3

(d) 测点4

通过计算结果和实测结果分析，可以得出：

1)通过将3种方法计算结果和实测拱顶沉降对比，固支梁模型挠度计算结果显著偏小，这是由于在实际施工过程中难以保证管棚结构与侧墙初期支护连接为固接，因此，固支梁模型挠度计算结果不具有参考价值；弹性地基梁模型和简支梁模型的计算结果相差较小，且与实测数据较符合。

3)从弯矩计算结果来看，在开挖宽度内，弹性地基梁模型计算结果处于固支梁模型和简支梁模型之间，这是由于简支梁和固支梁模型简化边界约束条件所导致。实际上，管棚在导洞侧壁位置处(2.2 m处)的情况既非"简支"也非"固支"，而是处于两者之间。

3 影响参数分析

本节分别针对不同的开挖跨度、土体性质(基床系数)、管棚钢管厚度、覆土厚度(荷载大小)、管径的力学模型，通过MATLAB程序进行理论计算，以探究不同的参数对管幕变形与受力情况的影响。

3.1 开挖区跨度

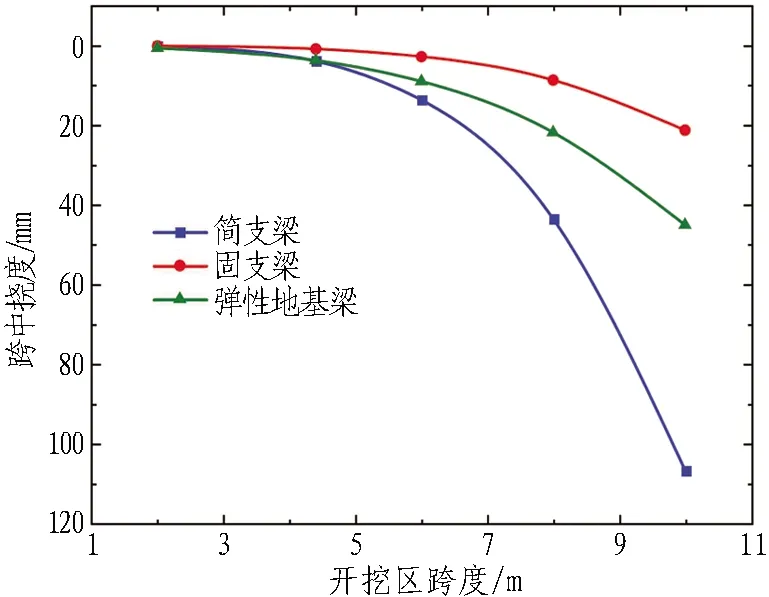
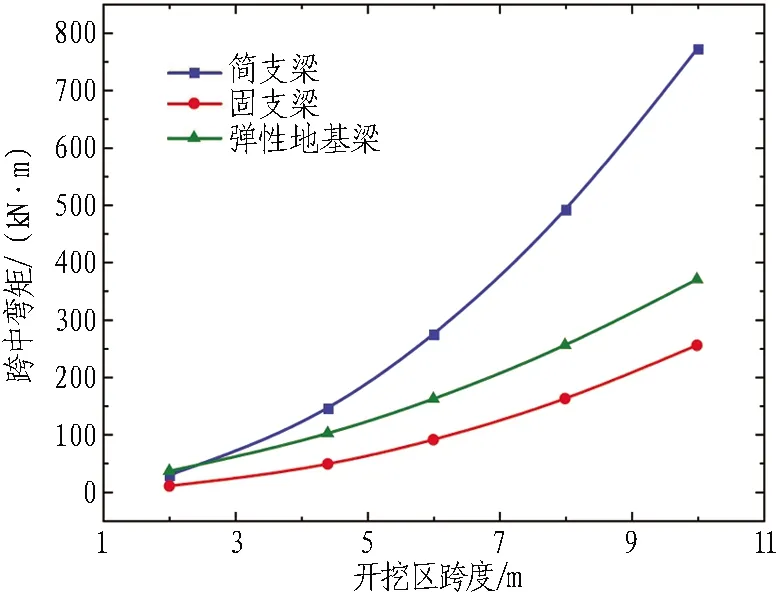
结合平安里站工程实例，建立开挖区跨度为2、4.4、6、8、10 m的力学模型并计算，以分析开挖区跨度对管棚受力变形的影响，计算结果如图11所示。

(a) 跨中挠度

(b) 跨中弯矩

从图11可以得出：

1)管棚的受力变形对开挖区跨度较为敏感。随着开挖区跨度变大，跨中挠度和跨中弯矩都显著增大，且逐渐加快。因此，可以通过减小跨度的方式(减小导洞尺寸、在跨中设置竖向支撑等)，显著改善管棚受力和变形情况。

2)弹性地基梁模型的计算结果大体处于简支梁模型与固支梁模型之间。与弹性地基梁模型相比，固支梁模型计算的跨中挠度和跨中弯矩均偏小，简支梁模型则均偏大。

3)在小跨度(小于5～6 m)情况下，弹性地基梁模型计算结果更接近简支梁模型；反之，则接近固支梁模型。

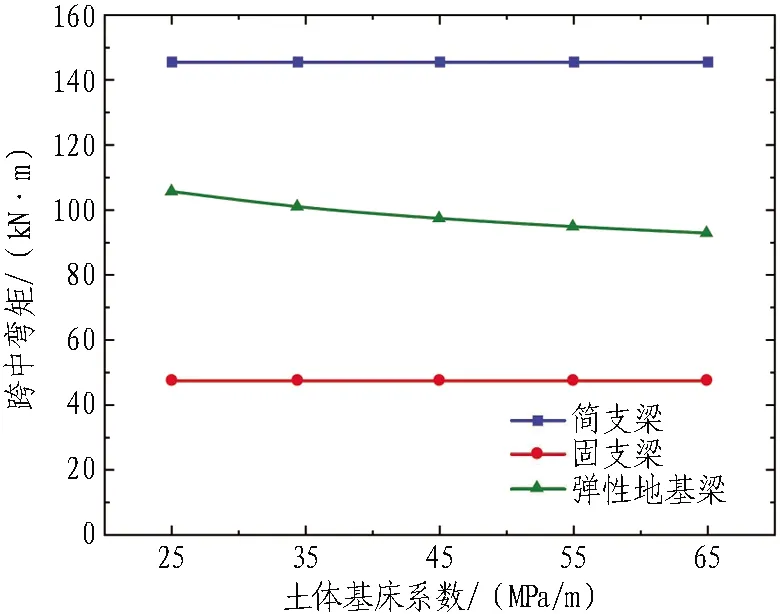
3.2 土体基床系数

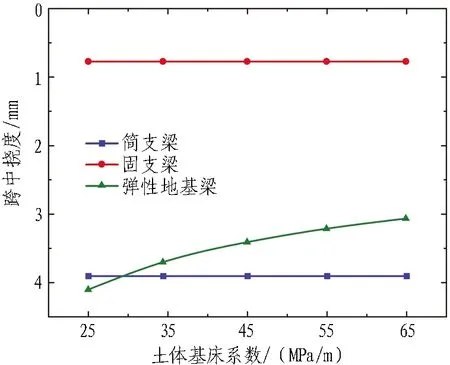
结合平安里站工程实例，建立基床系数为25、34.4、45、55、65 MPa/m的力学模型并计算，以分析土体基床系数对管棚受力变形的影响，计算结果如图12所示。

(a) 跨中挠度

(b) 跨中弯矩

从图12可以得出：

1)不同的基床系数下，弹性地基梁模型的跨中弯矩均处于简支梁模型和固支梁模型之间，而挠度计算结果均更接近于简支梁模型。

2)根据弹性地基梁模型计算结果，随着基床系数的提高，跨中挠度显著减小，但变化逐渐趋于平缓。这说明提高基床系数对管棚挠度有一定影响，但其效果会逐渐减小。

3)根据弹性地基梁模型计算结果，随着基床系数的提高，跨中弯矩略有减小，但减小幅度极小。这说明基床系数对管棚受力影响极小。

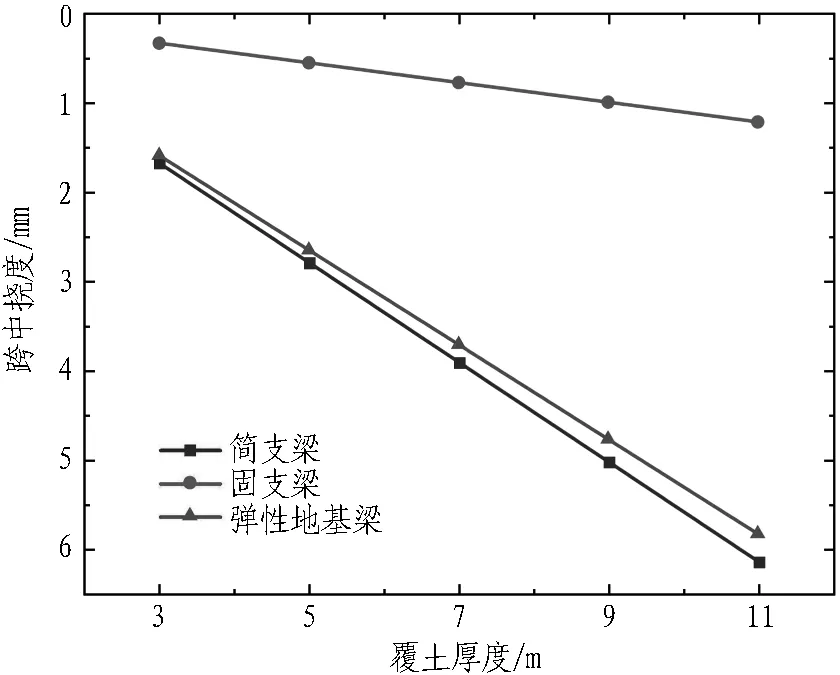
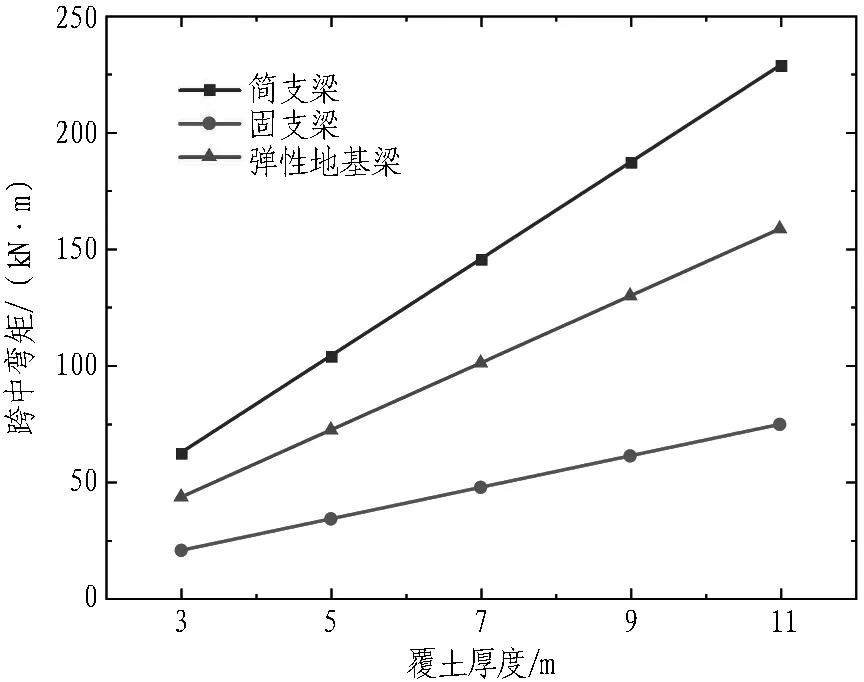
3.3 覆土厚度

结合平安里站工程实例，建立覆土厚度为3、5、7、9、11 m的力学模型并计算，以分析管棚上覆土厚度(上部荷载q)对管棚受力变形的影响，计算结果如图13所示。

(a) 跨中挠度

(b) 跨中弯矩

从图13可以得出：

1)在3种模型中，跨中挠度和跨中弯矩均随上覆土厚度(上部荷载q)线性增长。

2)弹性地基梁模型的跨中挠度计算值较为接近简支梁模型，而跨中弯矩一直处于简支梁和固支梁模型之间。相较于其他模型，简支梁模型的跨中弯矩偏安全。

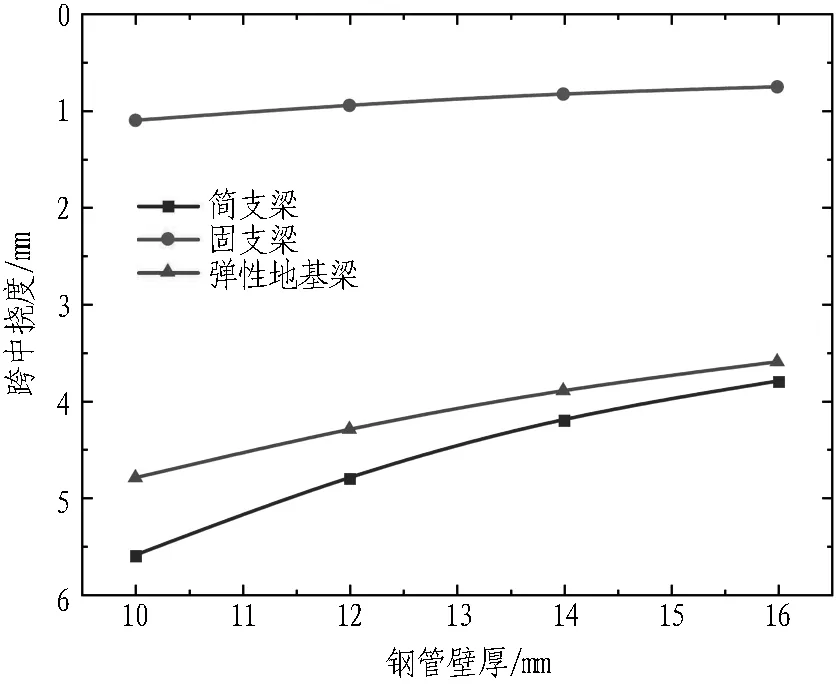
3.4 钢管壁厚

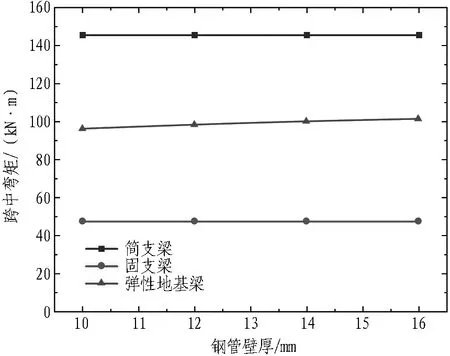
结合平安里站工程实例，建立管棚钢管壁厚分别为10、12、14、16 mm的力学模型并计算，以分析管棚钢管壁厚对管棚受力变形的影响，计算结果如图14所示。

(a) 跨中挠度

(b) 跨中弯矩

从图14可以得出：

1)不同的钢管壁厚条件下，弹性地基梁模型的跨中弯矩均处于简支梁模型和固支梁模型之间，而挠度结果更接近于简支梁模型。

2)根据弹性地基梁模型计算结果，随着钢管壁厚的增加，跨中挠度减小，但变化逐渐趋于平缓。这说明增加壁厚对减小挠度有一定效果，但其作用会逐渐减小。

3)根据弹性地基梁模型计算结果，随着钢管壁厚的增加，跨中弯矩变化幅度较小。

3.5 钢管管径

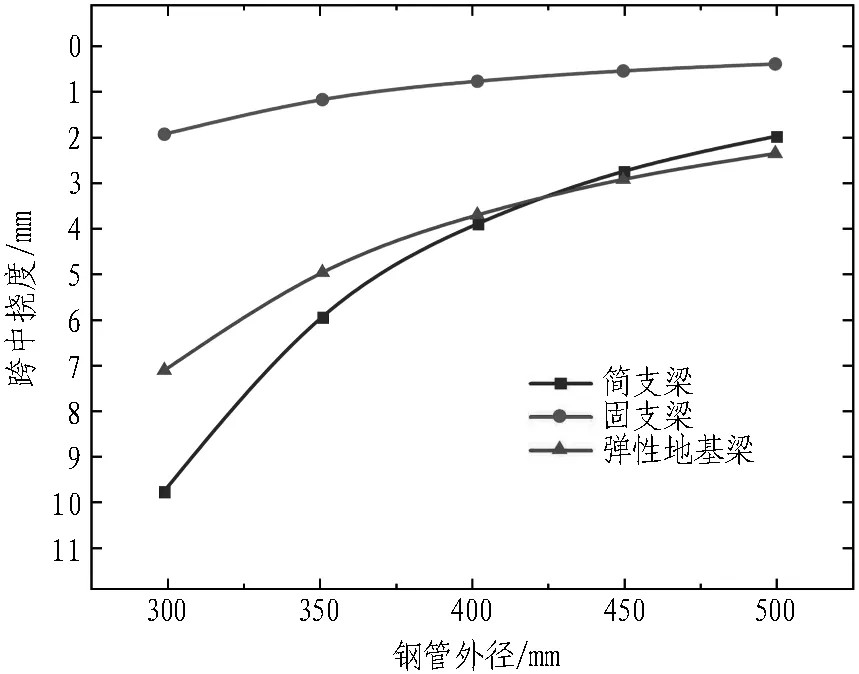
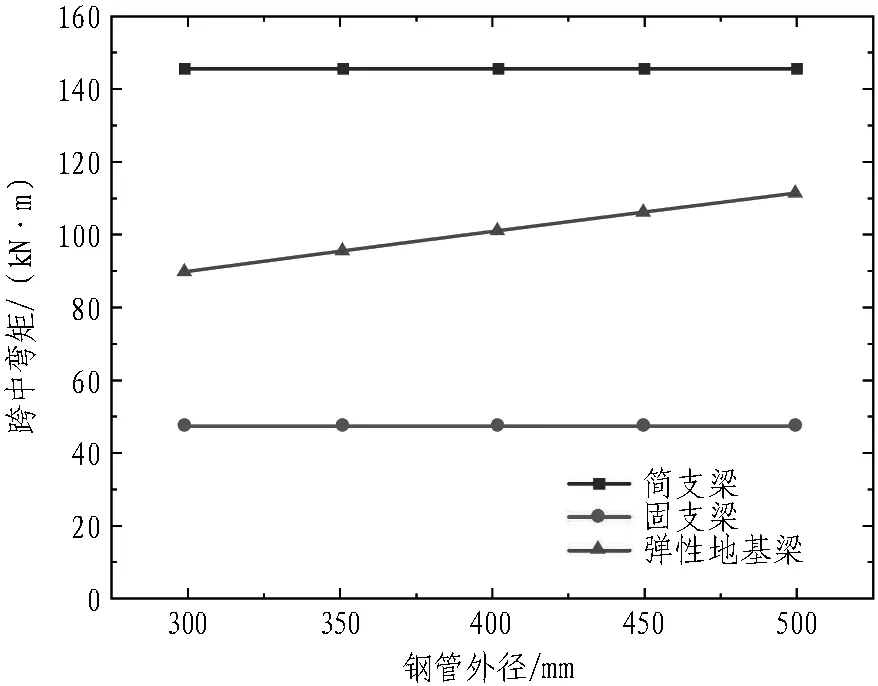
结合平安里站工程实例，建立管棚钢管管径为299、351、402、450、500 mm的模型并计算，以分析管棚钢管管径对管棚受力变形的影响，计算结果如图15所示。

(a) 跨中挠度

(b) 跨中弯矩

从图15可以得出：

1)增大管径可以大幅减小管棚钢管的跨中挠度。根据弹性地基梁模型计算结果，增大管径会使跨中弯矩略有增大。

2)弹性地基梁模型与简支梁模型的挠度计算结果较为接近，而固支梁模型的挠度计算结果偏小。相较于其他模型，简支梁模型的跨中弯矩偏安全。

4 结论与讨论

本文针对北京地铁平安里车站PBA工法的密布横向管棚，分别进行了简支梁、固支梁和弹性地基梁3种简化模型计算，并分析了不同参数对管棚受力变形的影响，得出的主要结论如下：

1)3种模型中，弹性地基梁模型和简支梁模型的变形计算结果均与实测数据较符合，说明变形计算中弹性地基梁和简支梁简化模型较为可靠。固支梁模型挠度计算结果显著偏小，这是因为在实际施工过程中难以保证管棚结构与侧墙初期支护连接为固接。

2)弹性地基梁模型计算的弯矩和跨中挠度均处于固支梁模型和简支梁模型计算结果之间。简支梁模型跨中弯矩偏大而两端弯矩偏小，固支梁模型则与此相反。

3)简支梁模型挠度计算结果与实测值较符合；相较于其他模型，简支梁模型的跨中弯矩值偏安全，且该模型计算过程简单。因此，推荐在实际工程中采用简支梁模型。

4)开挖跨度对管棚挠度和弯矩的影响极大。增大管径、提高基床系数、增加钢管壁厚对管棚弯矩影响较小，但对减小管棚挠度有明显作用。工程中可以通过减小跨度(减小导洞尺寸、在跨中设置竖向支撑等)的方式改善管棚的受力和变形；另外，可以通过增大钢管管径、壁厚，以减小管棚结构的变形，进而减小周围岩土扰动和地表沉降。

本文虽然通过解析方法模拟了导洞上方横向管棚的受力变形，得到了基本符合实测数据的计算结果，但未考虑弹性地基梁模型中初期支护结构对管棚的支撑和约束作用。下一步可以在连续梁的初期支护位置将土弹簧设置成不同的刚度，以更好地模拟初期支护的作用，分析不同的初期支护结构对管棚受力变形的影响。