冻融循环对季冻区隧道衬砌混凝土导热系数影响研究

李 伟， 张东淼， 叶 飞， 王思宇， 梁晓明

(1. 吉林省公路管理局， 吉林 长春 130021； 2. 长安大学公路学院， 陕西 西安 710064)

0 引言

导热系数是指单位温差、单位时间内通过单位面积的热量，它表征物体导热能力的大小。文献[1-2]表明衬砌混凝土的导热系数受混凝土孔隙率大小的影响，随着冻融循环次数的增加，衬砌导热系数不再为一常数，而是随着冻融循环的次数而改变的变量。为研究季冻区运营公路隧道的径向温度场分布规律，首先要得到衬砌导热系数随冻融循环次数变化而改变的规律。

导热系数作为主要的热力学基础参数之一，国内外学者对其确定方法已经进行了广泛研究。目前，导热系数的研究主要采用理论分析和数值模拟方法进行。

理论分析方面： 奚同庚等[3]根据导热的微观理论，发现复合材料各组分的相对含量对材料导热系数有一定影响，并验证了Eucken方程预测该类复合材料导热系数的有效性； D. Campbell-Allen等[4]研究发现孔隙率及含水量是混凝土导热系数的重要影响因子，并建立了用于预测混凝土材料导热系数的理论模型(Campbell-Allen and Thorne模型)； 刘为民等[5]提出了与土体饱和度有关的形状系数，推导出了以土体孔隙率和饱和度为自变量的土体导热系数计算公式； Zhang等[6]提出了一种用于预测多孔复合材料系数随机混合模型(RMM)； 张伟平等[7]分析了2相复合材料导热系数理论模型，对比发现干混凝土必须考虑不同介质之间界面热阻产生的影响，而饱和混凝土不需要考虑界面热阻的影响； 张枫等[8]总结了常用于计算混凝土导热系数的4种理论模型，并通过试验测定混凝土模型的导热系数，与理论计算结果进行对比，得出与实测值最接近的导热系数理论计算方法； 张伟平等[7]通过总结分析已有混凝土多相复合材料导热系数的理论计算公式，按照是否考虑不同介质间界面热阻等条件，将理论计算模型大致归纳为串联模型和并联模型(不考虑界面热阻)以及考虑界面热阻的Maxwell理论计算模型和不考虑界面热阻的Maxwell理论计算模型3类； J. C. Maxwell[9]基于远场理论(Far-Field methodology)，推导出了可根据2相复合材料中各单一介质导热系数和占比等参数计算该材料有效导热系数的计算公式； D. A. G. Bruggeman[10]根据J. C. Maxwell推导出的多相复合材料导热系数计算公式，通过考虑分散相粒子之间相互影响的作用，推导出了计算多相复合材料有效导热系数的隐式方程； 在此基础上，R. L. Hamilton等[11]研究发现，复合材料中各分散粒子的形状及2相单一介质的导热系数比值也会影响复合材料有效导热系数的计算结果，基于此种考虑，R. L. Hamilton等通过推导得出目前普遍应用于混凝土有效导热系数计算的Hamilton和Crosser理论计算模型。

数值模拟方面： 丁杨等[12]利用理论计算方法和COMSOL仿真软件的计算结果对比分析发现，2种方法得出的泡沫混凝土导热系数计算结果基本吻合； 张仲彬等[13]利用ANSYS有限元软件，基于多孔介质模型计算了污垢材料的有效导热系数，并分析了不同参数对污垢导热系数的影响； 赵育[14]利用ANSYS有限元软件，提出混凝土材料有效导热系数的细观数值模拟计算方法，并通过与文献计算结果对比，验证了该方法计算混凝土导热系数的可靠性； 李守巨等[15]利用ANSYS有限元模拟软件，研究了岩土材料导热系数与孔隙率的关系； 丁杨等[1]利用COMSOL仿真软件研究了混凝土材料导热系数与孔隙率的关系； 李守巨等[15]利用ANSYS有限元随机模拟断面的热流密度分布和稳态热传导傅里叶定律，通过APDL参数化语言赋值，计算了岩土材料导热系数与孔隙率之间的关系； 丁杨等[12]分别利用COMSOL软件仿真方法和理论计算方法获取了复合材料的导热系数，并与实测结果对比发现，COMSOL软件仿真结果与实测结果更加接近。

此外，田威等[16]利用CT扫描技术，研究了冻融循环下的混凝土试件内部细观孔隙的变化，发现混凝土试件的孔隙率随着冻融循环次数的改变而产生明显变化。

现有研究已经对材料导热系数进行了广泛的探索，但未深入研究孔隙率与导热系数的关系。本文在已有研究的基础上，对混凝土复合材料导热系数的计算方法进行研究，分析孔隙率与导热系数之间的关系，探讨季冻区运营隧道冻融循环次数对混凝土导热系数的影响。

1 影响机制

1.1 裂隙初次充水过程

在新建隧道衬砌混凝土的内部，存在着许多孔隙，孔隙率的大小与混凝土的配合比、水灰比、混凝土的搅拌工艺及养护温度和时间等因素有关。受施工工艺及养护条件等的限制，新建隧道衬砌混凝土内部存在微小裂缝。在热融期，衬砌背后的积水通过衬砌内部的渗水通道流入衬砌混凝土内部，如图1(a)所示。此过程为衬砌挂冰的初次充水过程。

1.2 裂隙初次扩张过程

当季冻区运营隧道进入冻结期后，渗流进入衬砌混凝土内部的裂隙水逐渐发生冻结。0 ℃水的密度为1 g/cm3，0 ℃冰的密度为0.9 g/cm3，同等质量的水冻结成冰，体积扩大约9%。则衬砌内部渗水通道内的水冻结成冰时，体积膨胀，体积较大的冰对渗水通道的四周产生了冻胀力。当冻胀力较大时，衬砌内部细观结构遭到破坏，导致渗水通道进一步扩张，混凝土内部裂隙劈裂，如图1(b)所示。此过程为衬砌裂隙受冻胀作用的初次扩张过程。

1.3 裂隙中二次充水及二次扩张过程

当季冻区运营隧道由冻结期转入热融期时，裂隙中的冰热融为水，体积减小，而受冻胀作用而扩张的裂隙体积不会减小。此时，衬砌背后积水会继续渗入衬砌裂隙中，直至裂隙中充满水，充水量的大小与初次冻胀导致衬砌内部裂隙扩张的体积大小有关。此过程为衬砌挂冰的二次充水过程。当隧道再次由热融期进入冻结期后，裂隙中的水会再次冻结成冰，体积变大，导致衬砌内部的裂隙受冻胀作用而再次扩张。

当衬砌背后的积水量充足时，衬砌混凝土内部的渗水通道或者裂隙会随着冻-融的反复交替而出现"扩张-充水-扩张..."的过程，直至裂隙在衬砌结构上贯通，裂隙中的水流至衬砌表面，在冻结期形成挂冰，如图1(c)所示。在衬砌宏观角度，这一过程可能导致衬砌结构出现由内而外贯通的渗水通道，表现为衬砌挂冰、边墙壁冰等冻害形式；在微观及细观角度，衬砌混凝土内部裂隙及孔隙在冻融交替作用下经过"扩张-充水-扩张"的过程后，衬砌混凝土的孔隙率势必较初始状态下的混凝土孔隙率增大。混凝土材料作为由骨料、砂浆和孔隙组成的多相复合材料，由冻融反复交替作用引起的混凝土孔隙率的改变势必导致混凝土复合材料导热系数的改变。

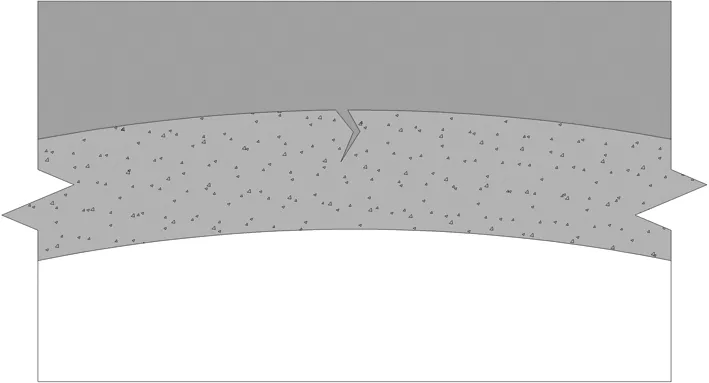
(a) 裂隙初次充水

(b) 裂隙初次扩张

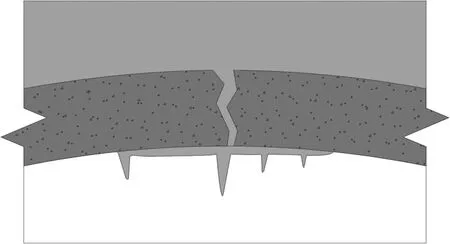
(c) 衬砌挂冰

2 混凝土导热系数计算模型

隧道内的混凝土衬砌是一种固液2相或者固液气3相多组分复合材料。隧道内衬砌发生冻害的2大基本条件是水和低温。为了便于研究，此处假定计算导热系数的混凝土孔隙内全部由水来填充，即假定混凝土材料为固液2相多组分复合材料。组成材料有砂浆、骨料、水。混凝土复合材料成分如图2所示，其中水为液相，砂浆和骨料组成混凝土材料的固相。假定混凝土材料为均质材料，即水、砂浆、骨料均匀且随机分布。此时，混凝土模型中的固相材料导热系数为定值，即从计算混凝土复合材料导热系数的角度来讲，可将固相材料视作一个整体模型。混凝土复合材料模型合成如图3所示。该复合材料的导热系数仅与液相的含量有关，此处液相含量即混凝土模型的孔隙率，因而推断冻融循环过程影响了液相含量，也即改变了模型的孔隙率。

(a) 骨料

(b) 砂浆

(c) 水(冰)

3 基于多孔介质模型的衬砌导热系数计算

为了简化衬砌混凝土导热系数的计算，可将衬砌混凝土简化为多孔介质模型，由不连续的孔隙、骨料以及连续的砂浆基质组成。为了研究冻融循环次数对衬砌导热系数的影响，假定衬砌混凝土中的孔隙、砂浆、骨料等均为非热物性材料，即其导热系数等热学参数不随温度的改变而改变，孔隙率的大小仅与冻融循环次数有关。

固相 液相 混凝土模型

由文献[7]可知，在对饱和状态下的混凝土导热系数计算时，可忽略不同单一介质之间界面热阻的影响。本文基于Hamilton and Crosser理论计算模型，对衬砌混凝土的有效导热系数进行计算。

该模型导热系数计算表达式如下：

(1)

(2)

式(1)-(2)中：λe为复合材料有效导热系数；λ1为连续相基质的导热系数；λ2为非连续相基体的导热系数；v2为非连续相基体的体积分数；α为式(1)中简化参数；n为第2相分散基粒在第1相连续基质中的几何分布函数，其值一般通过试验取得，根据文献[8]，n=3适用于球型微粒，因此本文取n=3。

以文献[16]中的混凝土试件为例，取混凝土试件尺寸为100 mm×100 mm×100 mm的立方体。混凝土配合比如表1所示。

表1 混凝土试件配合比

选取石灰岩为骨料原料，查找可知石灰岩的密度为2.7 g/cm3，计算可知骨料在混凝土试件中的体积占比约为0.406 9。

引用文献[16]中对不同冻融循环次数下的饱和混凝土试件进行的CT扫描结果可得，不同冻融循环次数下的混凝土试件总孔隙率如表2所示。

表2 不同冻融循环次数下的混凝土试件总孔隙率

由表2可以看出： 1)混凝土试件在经历0～50次冻融循环过程中，孔隙率随着冻融循环次数的增加而升高，该结果与本文对季冻区隧道冻害机制分析结果吻合，混凝土内部裂隙在冻融循环环境中，存在"扩张-充水-扩张"的过程，即随着冻融循环次数增多，混凝土内部孔隙受冻胀而逐渐扩张，从而导致混凝土试件的孔隙率逐渐升高； 2)混凝土试件在经历50～75次冻融循环过程中，孔隙率出现了下降。分析该过程中，混凝土内部孔隙已经增大到一定程度，孔隙体积增大，饱和状态下孔隙中的水量增大，冻胀作用下，水冻结成冰产生的冻胀力逐渐增大，而孔隙周围的孔隙壁越来越薄，在这种双重作用下，孔隙壁由于失稳而断裂，造成混凝土细观结构产生坍塌，从而导致混凝土试件的总孔隙率产生了一定程度的下降。这一孔隙率下降的过程，意味着混凝土结构已经遭到了破坏，与本文孔隙"扩张-充水-扩张"的过程并不矛盾，相反，孔隙率降低是孔隙"扩张-充水-扩张"过程的末期形态，反映到宏观角度，则混凝土试件可能会出现剥落、掉块等现象。由此分析可知，若冻融循环次数再增加，混凝土试件的孔隙率基本不再变化，或会出现微小的变化，因为混凝土内部孔隙结构已经失稳坍塌，孔隙壁不再承受冻胀力。

将以上参数代入式(1)和式(2)中，根据Hamilton和Crosser理论模型计算可得，不同孔隙率下混凝土试件的导热系数如表3所示。

表3 不同冻融循环次数下的混凝土试件总孔隙率及有效导热系数

理论计算得到的试件有效导热系数与冻融循环次数之间的关系如图4所示。

4 基于COMSOL仿真软件的混凝土有效导热系数数值模拟

为了验证理论计算结果的可靠性，本文利用COMSOL仿真软件，对混凝土试件进行有效导热系数的细观数值模拟计算。混凝土材料作为一种搅拌而成的复合材料，其内部非连续相的骨料和孔隙等均可看做无规则随机分布在连续相的砂浆中。为了更好地模拟混凝土试件，采用MATLAB软件中的随机函数"rand()"对混凝土试件中的骨料位置和孔隙位置进行计算。刘光廷等[17]利用非线性有限元技术，研究了混凝土破坏机制，且验证了混凝土随机骨料模型能够较好地模拟混凝土内部的细观分布； 吕钊[18]基于MATLAB中的程序语言，研究了二维和三维混凝土随机骨料生成和投放算法。

图4 试件有效导热系数与冻融循环次数的关系

本文利用COMSOL仿真软件传热模块中的稳态导热算法对混凝土试件有效导热系数进行细观数值模拟。混凝土有效导热系数细观数值模拟计算流程如图5所示。

4.1 建立混凝土随机骨料模型

本文基于MATLAB软件中的随机分布函数建立混凝土试件的随机分布模型，具体建模流程如图6所示。

4.1.1 混凝土随机分布模型参数定义

首先定义混凝土试件的尺寸为100 mm×100 mm×100 mm，混凝土试件作为3相复合材料，定义材料中砂浆、骨料和孔隙的基本参数，以及骨料和孔隙的尺寸。混凝土模型基本参数如表4所示。

其中，由于要测定的是冻融循环对混凝土试件导热系数的影响，因此假定混凝土模型为饱和状态，故孔隙中参数的定义实际上是0 ℃水的物理参数。

图6 MATLAB建立混凝土随机分布模型流程图

表4 混凝土模型基本参数

4.1.2 生成骨料、孔隙坐标

为简化计算，设定骨料和孔隙的形状均为球型，骨料的平均半径为10 mm ，误差为±1 mm； 孔隙的平均半径为3 mm，误差为±1 mm(实际上，由混凝土级配曲线可知，混凝土材料中骨料的尺寸并非定值，本文将骨料尺寸统一定义为平均尺寸，而孔隙的尺寸也并不固定)。利用MATLAB中的随机函数"rand()"和骨料、孔隙的体积总占比逐次计算，得出骨料和孔隙的坐标。

4.1.3 输出混凝土随机分布模型

确定好骨料和孔隙的坐标后，即可输出混凝土随机分布模型。

通过改变初始孔隙率的参数，即可生成不同孔隙率下的混凝土随机分布模型，将MTALAB生成的二维混凝土随机分布模型输出可视化。MATLAB生成的不同孔隙率混凝土随机分布模型如图7所示。

4.2 导热系数仿真计算

4.2.1 边界条件

利用MATLAB建立好混凝土随机分布模型后，即可通过内联程序导入COMSOL仿真软件中进行分析。由于前期在MATLAB对材料参数定义时，已确定了各材料的基本物理参数，如体积比热、密度、导热系数等。将模型导入COMSOL仿真软件后，只需补充边界条件和初始条件即可。参考实际导热系数测定仪的工作原理，设定该二维混凝土随机分布模型的上边界温度为30 ℃，为热板； 下边界温度为10 ℃，为冷板； 左右边界设定环境温度为20 ℃。

(a) 孔隙率0.138 7

(b) 孔隙率0.157 5

(c) 孔隙率0.187 0

(d) 孔隙率0.174 9

Fig. 7 Random distribution models of concrete with different porosities generated by MATLAB

4.2.2 网格划分及独立性检验

采用COMSOL自带的网格划分功能，并选用常规网格即可： 最大单元尺寸为6.7 mm，最小单元尺寸为0.03 mm； 最大单元生长率为1.3，其曲率因子为0.3； 狭窄区域解析度为1。利用该参数对4个不同孔隙率的混凝土随机分布模型进行网格划分。混凝土导热系数计算模型网格划分如图8所示。为了使计算结果更为精确，开展对划分网格的独立性检验，检验结果显示网格划分完好。

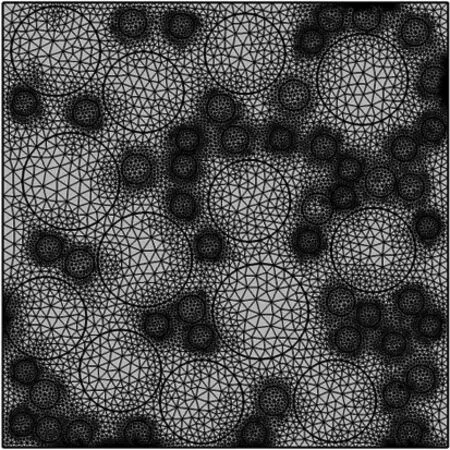
(a) 孔隙率0.138 7

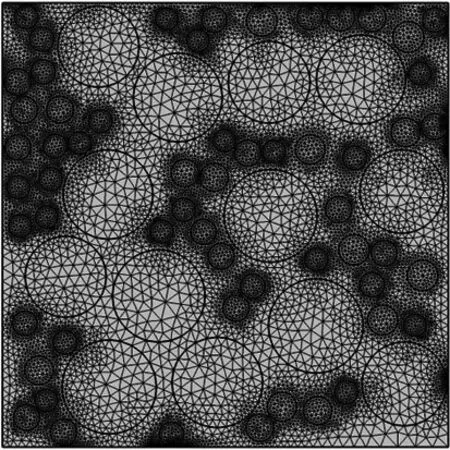
(b) 孔隙率0.157 5

(c) 孔隙率0.187 0

(d) 孔隙率0.174 9

4.2.3 稳态传热分析

利用COMSOL仿真软件中的固体传热模块，即可对模型开展混凝土试件有效导热系数测定仿真模拟试验。混凝土导热系数软件运行结果如图9所示。

(a) 孔隙率0.138 7

(b) 孔隙率0.157 5

(c) 孔隙率0.187 0

(d) 孔隙率0.174 9

4.2.4 试验结果分析

根据仿真试验结果，对模型的导热系数进行计算。COMSOL仿真软件中，稳态固体传热模块默认传热方程如式(3)所示。

(3)

(4)

式中：λ为材料的导热系数，W/(m·K)。

根据式(3)与式(4)，可以计算出混凝土试样的有效导热系数。4个不同孔隙率的混凝土随机分布模型有效导热系数计算结果如表5和图10所示。

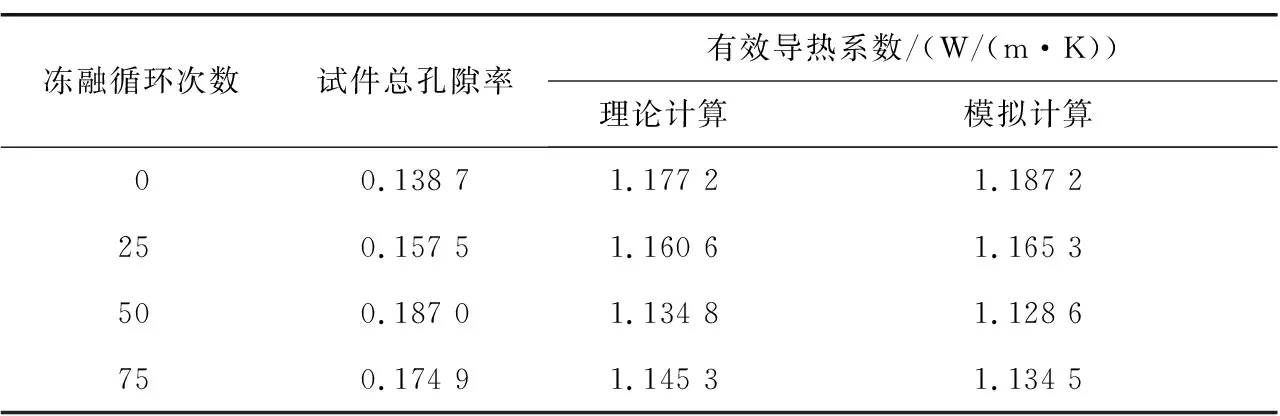
表5 导热系数计算结果对比

由表5和图10可知： 1)仿真试验计算结果与Hamilton and Crosser理论计算结果中，模型的有效导热系数随着冻融循环次数变化的发展趋势基本一致； 2)混凝土有效导热系数与冻融循环次数之间为非线性关系。

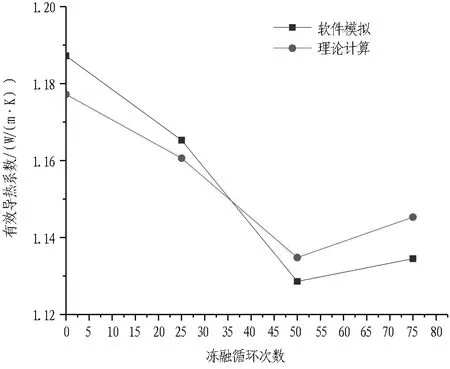
图10 有效导热系数计算结果对比

但利用COMSOL仿真软件计算得出的有效导热系数与Hamilton and Crosser理论计算结果存在一定偏差。初步分析，造成这种偏差的原因可能有以下几种。

1)基于Hamilton and Crosser模型计算得出的混凝土导热系数是在绝对理想的条件下，仅通过复合材料中各单一材料的占比计算得出的结果，未考虑单一骨料、孔隙的大小及在混凝土中的几何分布状况。

2)基于MATLAB得出的混凝土随机分布模型中，固定了单一骨料及孔隙的半径大小，但也正是固定了单一骨料及孔隙的大小，导致生成的混凝土随机分布模型中，骨料及孔隙占比可能与预期骨料及孔隙占比之间存在微小偏差。

3)利用COMSOL仿真软件计算混凝土试件的导热系数，是基于MATLAB生成的混凝土随机分布模型，模型中骨料和孔隙的分布也会影响混凝土试件的传热路径，导致计算结果存在误差。

利用3次函数，对冻融循环次数与衬砌混凝土有效导热系数之间的函数关系式进行拟合，可得：

式(5)-(6)中：λ为衬砌混凝土的有效导热系数，W/(m·K)；N为冻融循环次数；R2为相关系数。

式(5)与式(6)分别为理论计算与仿真计算得出的3次函数曲线拟合结果，R2均等于1，说明在0≤N≤75时曲线拟合度较高。

5 结论与体会

本文总结了各类混凝土导热系数计算理论模型，并分析了其特点，并针对本研究中的衬砌混凝土在冻融环境下的特点，选取了适用于本文的混凝土导热系数计算模型--Hamilton and Crosser理论模型，计算了受冻融循环作用下不同孔隙率的混凝土试件的有效导热系数。主要结论与体会如下：

1)利用COMSOL中的传热方程，对混凝土随机分布模型的有效导热系数进行了逆运算，得到不同冻融循环作用下不同孔隙率的混凝土模型的有效导热系数，并通过将该结果与基于Hamilton and Crosser理论计算模型得出的相应孔隙率下混凝土试件的有效导热系数进行对比，验证了计算结果的可靠性，并通过对曲线拟合得到混凝土试件有效导热系数与冻融循环次数之间的非线性函数关系。

2)通过对计算结果的对比分析，发现衬砌导热系数在冻融循环作用下，初期导热系数随着冻融循环次数的增加而下降，中期随着冻融循环次数的逐渐增加，导热系数出现较小程度的增大，分析其原因可能是冻融循环导致孔隙结构破坏坍塌，从而导致衬砌导热系数出现较小程度的反弹趋势。

3)与以往研究相比，本文建立了冻融循环次数与衬砌导热系数之间的联系，为季冻区公路隧道的设计及养护提供了新的思路，使季冻区公路隧道的设计及养护更加科学合理。目前本文尚有许多不足，如冻融循环次数较少，可供研究的数据量小等，下一步将开展冻融循环试验以验证理论计算结果，并进一步分析冻融循环过程中裂缝扩张的机制。